200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P4)

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số  y= x³-3mx²+ 3m³ có hai điểm cực trị A và B  sao cho tam giác OAB  có diện tích bằng 48.

Cho hàm số y= x⁴-2( m+1)x²+ m ( C). Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số C có ba điểm cực trị A: B; C  sao cho  OA= BC ;   trong đó O  là gốc tọa độ,  A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.

Tìm tất cả các giá trị thực của tham số m  để đồ thị hàm số  y= x³- 3mx²+ 4m³   có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y=0.

Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x³-3mx²+ 3( m²-1) x- m³+ m  có cực trị, đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng $\sqrt{2}$ lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.

Tính tích tất cả các giá trị thực của tham số m để đồ thị hàm số y =m x³- 3mx²+ 3m-3 có hai điểm cực trị A; B  sao cho 2AB²- ( OA²+ OB²) =20 .

Cho hàm số y= x³-3x²   .Tìm tất cả các giá trị thực tham số m  để đường thẳng đi qua 2 điểm cực trị của đồ thị C tạo với đường thẳng x+ my+ 3=0  một góc α biết cosα= 4/5.

Có giá trị của tham số m  để đồ thị hàm số y= x⁴-4( m-1) x²+2m-1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. Hỏi số nguyên nào gần với số m nhất?

Tìm tất cả các giá trị thực của tham số m để điểm M( 2m³; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số  y= 2x³-3( 2m+ 1) x²+ 6m( m+1) x+1 (C)  một tam giác có diện tích nhỏ nhất.

Với giá trị nào của tham số m thì hàm số $y=\sin \left(x\right)-\cos \left(x\right)+2017\sqrt{2}mx$ đồng biến trên R.

Cho hàm số $f\left(x\right)=\frac{x^3}{3}+(4-m)\frac{x^2}{2}+(5-2m)x+m^2+3,$ với m là tham số thực. 
 Hàm số  $g\left(x\right)=\frac{x^2+4x+5}{x+2}$ có đồ thị C và bảng biến thiên sau:

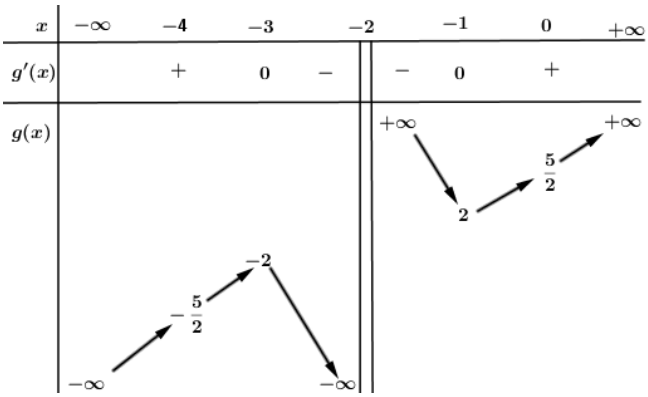
Tìm m sao cho hàm số f(x)  đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1

Cho hai số thực x, y thỏa mãn x≥ 0; y≥1 ; x+ y= 3 . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P= x³+ 2y²+ 3x²+ 4xy- 5x  lần lượt bằng:

Cho các số thực x; y thõa mãn x≥0; y≥0  và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m  của biểu thức $S=(4x^2+3y)(4y^2+3x)+25xy$ là:

Có bao nhiêu  giá trị nguyên của tham số m sao cho đồ thị của hàm số $y=\frac{x+1}{\sqrt{m{x}^2+1}}$  có hai tiệm cận ngang.

Tìm tất cả các giá trị thực của tham số m  sao cho đồ thị của hàm số $y=\frac{\sqrt{1-x}}{x-m}$  có tiệm cận đứng.

Tìm tất cả các giá trị thực của tham số m  sao cho đồ thị của hàm số $y=\frac{x+1}{x^3-3x^2-m}$  có đúng một tiệm cận đứng.

Cho hàm số $y=\frac{2x+1}{x-1}$   có đồ thị C. Gọi M  là một điểm bất kì trên C. Tiếp tuyến của C tại M  cắt các đường tiệm cận của C  tại A và B . Gọi I  là giao điểm của các đường tiệm cận của C . Tính diện tích của tam giác IAB.

Tìm tất cả các tiệm cận đứng của đồ thị hàm số $y=\frac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}$

Tìm tập hợp tất cả các giá trị của tham số thực của m để hàm số

Y= ln( x²+ 1) –mx+1 đồng biến trên  R.

Gọi d là đường thẳng đi qua điểm A( -1; 0)  với hệ số góc k . Tìm k  để đường thẳng d cắt đồ thị hàm số C: y= x³-3x²+  4  tại ba điểm phân biệt A; B; C  và tam giác OBC  có diện tích bằng  1?