20 câu hỏi
Tìm các giá trị của tham số m để đồ thị hàm số y= 2x3+ 3( m-3) x2+ 11- 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C( 0; -1) thẳng hàng
-2
-3
3
4
Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x3-3mx+ 2 cắt đường tròn tâm I (1; 1) bán kính bằng 1 tại 2 điểm A và B mà diện tích tam giác IAB lớn nhất .
m = 1±22.
m = 1±32.
m = 1±52.
m = 1±62.
Cho hàm số y= f( x) . Hàm số y= f’ (x) có đồ thị như hình vẽ.
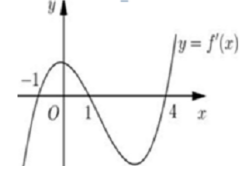
Hàm số y= f( x2) có bao nhiêu khoảng nghịch biến.
5
3
2
4
Cho hàm số y= f( x) ( x-1) liên tục trên R và có đồ thị như hình vẽ.
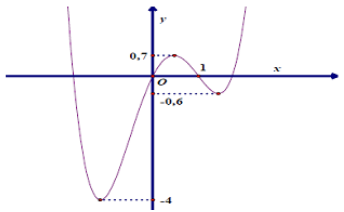
Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x - 1| = m có số nghiệm lớn nhất
( -0, 6; 0]
(-0,6; 0)
(0; 0,06)
( 0; 0,6)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
0; 3
2; 4
0; 2
1; 3
Cho hàm số y= f( x) =ax4+ bx3+ cx2+ dx+ e và hàm số y= f’( x) có đồ thị như hình vẽ bên. Biết f( b) < 0 , hỏi đồ thị hàm số y= f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
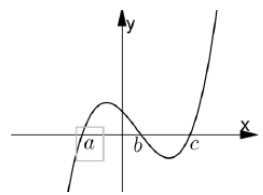
1
2
3
4
Tìm m để hàm số nghịch biến
-154<m≤0
Cho hàm số y= x3- 6x2+ 3( m+ 2) x-m-6. Hỏi có mấy giá trị nguyên của m để hàm số có 2 cực trị cùng dấu.
4
5
6
3
Cho hàm số y= 2x3- 9x2+ 12x+m. Giả sử đồ thị hàm số có hai điểm cực trị là A, B đồng thời A, B cùng với gốc tọa độ O không thẳng hàng. Khi chu vi tam giác OAB nhỏ nhất thì m bằng bao nhiêu?
-11/3.
-13/ 3
-14/ 3
8/3
Với giá trị nào của m, đồ thị hàm số có đúng hai đường tiệm cận?
mọi m
Cho hàm số y= x4-2mx2+ m-1. Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm .
m=0
m=1
m= 1;2
m= 0;1
Cho hàm số y= f( x) có đạo hàm Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV.
1
2
3
4
Tính tổng các giá trị nguyên của m để hàm số y= x8+ (m-2) x5- ( m2- 4) x4+ 1 đạt cực tiểu tại x= 0
3.
5.
4.
2.
Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số trên [ 0; ln4] bằng 6 .
3.
4.
1.
2.
Cho hàm số có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận của (C) . Xét tam giác đều ABI có hai đỉnh A; B thuộc (C) , đoạn thẳng AB có độ dài bằng
2.
Tính tổng các giá trị của tham số m để đồ thị hàm số: y= có ba điểm cực trị . Đồng thời ba điểm cực trị đó cùng với gốc tọa độ tạo thành 1 hình thoi.
Không tồn tại m.
2
1/4
9/4
Có bao nhiêu giá trị nguyên của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
0
1
2
3
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số trên đoạn [ 0; 2] không vượt quá 15 ?
4
6
5
8
Cho hàm số có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt đồ thị ( C) tại hai điểm phân biệt M( x1; y1) và N( x2; y2) (M; N khác A) sao cho y2- y1= 8( x2- x1).
0
2
3
5
Cho hàm số . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
4
5
6
3






