20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 7: Lập phương của một tổng hay một hiệu (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn, yêu cầu chọn phương án đúng nhất)
Đẳng thức nào sau đây là đúng?
\({\left( {a - b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} - {b^3}.\)
\({\left( {a - b} \right)^3} = - {a^3} + 3{a^2}b + 3a{b^2} - {b^3}.\)
\({\left( {a - b} \right)^3} = - {a^3} + 3{a^2}b - 3a{b^2} - {b^3}.\)
\({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}.\)
Cho đẳng thức \(8{x^3} + 12{x^2} + 6x + 1 = ...\) Điền vào dấu “...” để đẳng thức đúng.
\({\left( {8x + 1} \right)^2}.\)
\({\left( {2x + 1} \right)^2}.\)
\({\left( {x + 2} \right)^3}.\)
\({\left( {2x + 1} \right)^3}.\)
Khai triển \({\left( {a - \frac{1}{3}} \right)^3}\) ta được một đa thức có bao nhiêu hạng tử?
\(5.\)
\(4.\)
\(3.\)
\(2.\)
Giá trị của biểu thức \({101^3} - 3 \cdot {101^2} + 302\) là:
\({100^3}.\)
\({101^3}.\)
\({99^3}.\)
\({101^2}.\)
Viết đa thức \({m^3} + 9{m^2}n + 27m{n^2} + 27{n^3}\) dưới dạng lập phương của một tổng ta được:
\({\left( {3m + n} \right)^3}.\)
\({\left( {m + 3n} \right)^3}.\)
\({\left( {3m + 3n} \right)^3}.\)
\({\left( {\frac{1}{3}m + 3n} \right)^3}.\)
Cho đẳng thức \({a^3} + {b^3} = {\left( {a + b} \right)^3} - ...ab\left( {a + b} \right).\) Số thích hợp để điền vào dấu “...” để được đẳng thức đúng là:
\(1.\)
\(2.\)
\(3.\)
\( - 3.\)
Biểu thức \({x^3} - 3\left( {{x^2} + 1} \right) + 3x + 2\) viết được dưới dạng nào dưới đây?
\({\left( {x + 1} \right)^3}.\)
\({\left( {x - 1} \right)^3}.\)
\({x^3} - 1.\)
\({\left( {1 - x} \right)^3}.\)
Giá trị của biểu thức \(A = {x^3} + 9{x^2} + 27x + 27\) tại \(x = 97\) là:
\({97^3}.\)
\({98^3}.\)
\({100^3}.\)
\({99^3}.\)
Bác Minh gửi vào ngân hàng \(120\) triệu đồng theo thể thức lãi kép theo định kì với lãi suất \(x\) mỗi năm (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp). Biểu thức \(S = 120{\left( {1 + x} \right)^3}\) (triệu đồng) là số tiền bác Minh nhận được sau ba năm. Khai triển biểu thức \(S\) thành đa thức theo \(x\) ta được:
\(S = 120{x^3} + 360{x^2} + 360x + 120.\)
\(S = 120{x^3} + 360{x^2} - 360x + 120.\)
\(S = 120{x^3} + 360{x^2} - 360x.\)
\(S = 120{x^3} + 360{x^2} + 120.\)
Nếu \({x^3} + 3xy\left( {x + y} \right) = - {y^3}\) thì:
\(x = - y.\)
\(x = y.\)
\(x = 2y\)
\(x = - 2y\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, mỗi câu hỏi có 4 ý khẳng định, yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định)
Cho biểu thức \(P = {\left( {x - 1} \right)^3} + 3{\left( {x - 1} \right)^2}\left( {x + 1} \right) + 3\left( {x - 1} \right){\left( {x + 1} \right)^2} + {\left( {x + 1} \right)^3}\).
a) Thu gọn được biểu thức \(P = 6{x^3}\).
b) Giá trị biểu thức P tại \(x = 2\) bằng \(64.\)
c) Với đa thức \(B = - 8{x^3} + 5\) thì biểu thức \(P + B\) không phụ thuộc vào giá trị của biến.
d) Có hai giá trị của x để \(P = 0.\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Từ một khối lập phương có độ dài cạnh là \(3x + 2{\rm{ }}\left( {{\rm{cm}}} \right),\) người ta cắt bỏ một khối lập phương có độ dài cạnh \(x + 2{\rm{ }}\left( {{\rm{cm}}} \right)\) (như hình vẽ).
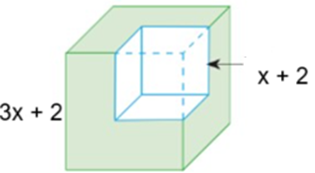
a) Thể tích của khối lập phương ban đầu là \({\left( {3x + 2} \right)^2}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right){\rm{.}}\)
b) Thể tích của khối lập phương bị cắt đi là \({\left( {x + 2} \right)^3}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right){\rm{.}}\)
c) Thể tích phần còn lại là \(26{x^3} + 48{x^2} + 20x\,\;\left( {{\rm{c}}{{\rm{m}}^3}} \right){\rm{.}}\)
d) Nếu \(x = 1{\rm{ cm}}\) thì thể tích phần còn lại của khối hộp là \(80{\rm{ c}}{{\rm{m}}^3}{\rm{.}}\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Cho hai số \(a,\;b\) thỏa mãn \({a^2} + {b^2} = 25;\;ab = 12\) và \(a > b > 0.\)
a) Tổng hai số a và b bằng \(5.\)
b) \(a - b = 1.\)
c) \({a^3} + 3{a^2}b + 3a{b^2} + {b^3} = 112.\)
d) \({a^3} - 3{a^2}b + 3a{b^2} - {b^3} = 1.\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Bác An dự định làm một khối hình lập phương có cạnh là \(10{\rm{ cm}}{\rm{.}}\) Sau khi xem xét, bác An đã tăng độ dài cạnh khối lập phương thêm \(x{\rm{ }}\left( {{\rm{cm}}} \right).\)
a) Cạnh của khối lập phương mới là là \(x + 10{\rm{ }}\left( {{\rm{cm}}} \right).\)
b) Thể tích của hình lập phương mới là \({\left( {x + 10} \right)^3}\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
c) Thể tích phần tăng thêm của khối lập phương mới so với khối lập phương bác An dự định gấp lúc ban đầu là \({x^3} + 30{x^2} + 300\,\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
d) Nếu thể tích phần tăng thêm của khối lập phương mới so với khối lập phương bác An dự định gấp lúc ban đầu là \(400\;{\rm{c}}{{\rm{m}}^3}\) thì độ dài cạnh của khối lập phương mới là \(11\;{\rm{cm}}.\)
yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Cho hai biểu thức \(A = {\left( {y - x} \right)^3} + x\left( {3{y^2} + {x^2}} \right),\;B = {\left( {2 - y} \right)^3} + 3y + 1 + {y^3}.\)
a) Thu gọn đa thức A được \(A = {y^3}.\)
b) Thu gọn đa thức B được \(B = 6{y^2} - 9y + 9.\)
c) Đa thức \(3A - B\) không chia hết cho \(3\) với mọi giá trị của \(x,\;y.\)
d) \(A + B\) là đa thức bậc có bốn hạng tử.
Phần III. Trắc nghiệm trả lời ngắn
Gồm 5 câu hỏi, mỗi câu hỏi yêu cầu đưa ra đáp án là một con số, tối đa có 4 kí tự, tính cả kí tự dấu và kí tự dấu phẩy
Khi rút gọn biểu thức \({\left( {1 + 2x} \right)^3} + {\left( {2x - 1} \right)^3}\) ta thu được một đa thức có bao nhiêu hạng tử?
Với giá trị nào của x thì \({\left( {2x - 3} \right)^3} - 4x\left( {2{x^2} - 9x + 3} \right) = 57?\)
Cho số tự nhiên m. Biết rằng, m chia cho 3 dư 2, hỏi \({m^3}\) chia cho 3 có số dư là bao nhiêu?
Cho hai số thực \(x,\;y\) thỏa mãn \(x + y = 6\) và \(xy = 8.\) Giá trị của biểu thức \({x^3} + {y^3}\) bằng bao nhiêu?
Cho hai số thực \(x,\;y\) sao cho \(x + y = 2.\) Tính giá trị của biểu thức \({x^3} + 6xy + {y^3}.\)



