20 câu trắc nghiệm Toán 8 Kết nối tri thức Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Đẳng thức nào sau đây là đúng?
\({a^2} - 4{b^2} = {\left( {a - 2b} \right)^2}.\)
\({a^2} - 4{b^2} = {\left( {2a - b} \right)^2}.\)
\({a^2} - 4{b^2} = \left( {a - 2b} \right)\left( {a + 2b} \right).\)
\({a^2} - 4{b^2} = \left( {2b - a} \right)\left( {2b + a} \right).\)
Cho đẳng thức \({x^2} + 4x + 4 = ...\) Điền vào dấu “...” để đẳng thức đúng.
\({\left( {x + 4} \right)^2}.\)
\({\left( {2x + 1} \right)^2}.\)
\({\left( {4x + 1} \right)^2}.\)
\({\left( {x + 2} \right)^2}.\)
Khai triển \({\left( {2a - \frac{1}{2}} \right)^2}\) ta được một đa thức có bao nhiêu hạng tử?
\(5.\)
\(2.\)
\(3.\)
\(4.\)
Giá trị của biểu thức \(46 \cdot 54\) là:
\(2\;484.\)
\(2\;494.\)
\(2\;474.\)
\(2\;504.\)
Đa thức \(\frac{1}{4}{x^2} - 36\) được viết dưới dạng tích của hai thức nào sau đây?
\(\frac{1}{2}x + 6\) và \(\frac{1}{2}x - 6.\)
\(\frac{1}{2}x + 6\) và \(6 - \frac{1}{2}x.\)
\(\frac{1}{4}x + 6\) và \(\frac{1}{4}x - 6.\)
\(\frac{1}{4}x + 6\) và \(6 - \frac{1}{4}x.\)
Viết biểu thức \(\left( {2a - 6} \right)\left( {2a + 6} \right) - 4{a^2} + 3a\) dưới dạng đa thức, ta thu được đa thức bậc mấy?
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Biểu thức \(4{x^2}{y^2} - 12xy + 9\) viết được dưới dạng nào dưới đây?
\({\left( {2xy + 3} \right)^2}.\)
\(\left( {2xy - 3} \right)\left( {2xy + 3} \right).\)
\({\left( {2xy - 3} \right)^2}.\)
\(\left( {3 - 2xy} \right)\left( {3 + 2xy} \right).\)
Giá trị của biểu thức \(A = {x^2} - 100x + 2\;500\) tại \(x = 51\) là:
\(2.\)
\(4.\)
\(1.\)
\( - 2.\)
Chọn đáp án đúng trong các đáp án dưới đây.
\({x^2} - 2x + 2 \ge 1\) với mọi giá trị thực của \(x.\)
\({x^2} - 2x + 2 < 1\) với mọi giá trị thực của \(x.\)
\({x^2} - 2x + 2 \ge 2\) với mọi giá trị thực của \(x.\)
\({x^2} - 2x + 2 \le 0\) với mọi giá trị thực của \(x.\)
Cho hai số \(a,\;b\) thỏa mãn \(a + b = 12\) và \(a - b = 2\). Giá trị của biểu thức \({a^2} - {b^2}\) là:
\(20.\)
\(24.\)
\(22.\)
\(26.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, mỗi câu hỏi có 4 ý khẳng định, yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định)
Cho biểu thức \(P = {\left( {2x + 3} \right)^2} + {\left( {3x - 7} \right)^2} + 2\left( {2x + 3} \right)\left( {3x - 7} \right)\).
a) Thu gọn được biểu thức \(P = {\left( {5x - 4} \right)^2}\).
b) Giá trị biểu thức P tại \(x = 2\) bằng \(6.\)
c) Cho \(B = 25{x^2} - 30x + 9,\) có hai giá trị của x để \(P - B = 0.\)
d) Có hai giá trị của x để \(P < 0.\)
Yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Trên một khu vườn hình vuông có cạnh bằng \(40{\rm{ m}}\) (như hình vẽ), người ta định trồng cây ăn quả xung quanh vườn có bề rộng \(x{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
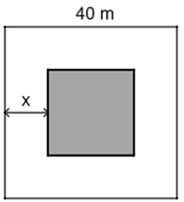
a) Diện tích của khu vườn là \(1\;600{\rm{ }}{{\rm{m}}^2}{\rm{.}}\)
b) Độ dài cạnh khu đất còn lại là \(40 - x{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
c) Diện tích khu đất còn lại là \({\left( {40 - x} \right)^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
d) Nếu diện tích trồng cây ăn quả là \(576{\rm{ }}{{\rm{m}}^2}\) thì bề rộng phần trồng cây ăn quả xung quanh vườn bằng \(2{\rm{ m}}{\rm{.}}\)
Yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Cho hai số \(a,\;b\) thỏa mãn \({a^2} + {b^2} = 20;\;ab = 8\) và \(a > b > 0.\)
a) Tổng hai số a và b bằng \(6.\)
b) \(a - b = 2.\)
c) \({a^2} - {b^2} = 16.\)
d) \({a^4} - {b^4} = 240.\)
Yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Từ một miếng bìa hình tròn (như hình vẽ) có bán kính \(R{\rm{ }}\left( {{\rm{cm}}} \right),\) người ta khoét một hình tròn ở giữa có bán kính \(r{\rm{ }}\left( {{\rm{cm}}} \right),r < R.\)
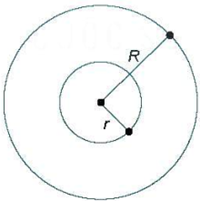
a) Diện tích miếng bìa hình tròn bán kính \(R{\rm{ }}\left( {{\rm{cm}}} \right)\) là \(2\pi R{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
b) Diện tích miếng bìa hình tròn bán kính \(r{\rm{ }}\left( {{\rm{cm}}} \right)\) bị khoét đi là \(\pi {r^2}\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
c) Diện tích phần còn lại của miếng bìa là \(\pi \left( {R - r} \right)\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
d) Nếu tổng hai bán kính là \(20\;cm\) và hiệu hai bán kính là \(6\;cm\) thì diện tích phần còn lại của miếng bìa là \(182\pi \;c{m^2}.\)
Yêu cầu lựa chọn đúng hoặc sai cho mỗi khẳng định
Cho hai biểu thức \(A = {\left( {x + 3y} \right)^2} + {\left( {3x - y} \right)^2},\;B = \left( {x + 2y} \right)\left( {x - 2y} \right) + 3{x^2}.\)
a) Thu gọn đa thức A được \(A = 4{x^2} + 4{y^2}.\)
b) Thu gọn đa thức B được \(B = 4{x^2} - 4{y^2}.\)
c) Đa thức \(A - B\) không chia hết cho 2 với mọi giá trị của \(x,\;y.\)
d) \(A \cdot B = 40\left( {{x^4} - {y^4}} \right).\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, mỗi câu hỏi yêu cầu đưa ra đáp án là một con số, tối đa có 4 kí tự, tính cả kí tự dấu và kí tự dấu phẩy
Điền số thích hợp vào dấu “…” để được đáp án đúng: \({\left( {{a^2} + {b^2}} \right)^2} - {\left( {{a^2} - {b^2}} \right)^2} = ...{a^2}{b^2}.\)
Với giá trị nào của x thì \(16{x^2} - {\left( {4x - 5} \right)^2} = 15?\)
Cho số tự nhiên m. Biết rằng, m chia cho 3 dư 2, hỏi \({m^2}\) chia cho 3 có số dư là bao nhiêu?
Rút gọn biểu thức \({\left( {x - y + z} \right)^2} - {\left( {x - y} \right)^2} - 2\left( {x - y} \right)z\) thu được đa thức có bao nhiêu hạng tử?
Cho hai số \(a > b > 0\) sao cho \({\left( {a - b} \right)^2} = 25\) và \(ab = 14.\) Tính giá trị của biểu thức \(a + b.\)




