20 CÂU HỎI
I. Nhận biết
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
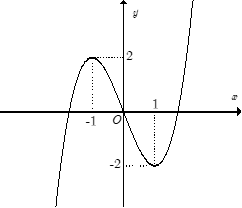
A. y = x3 – 3x.
B. y = −x3 + 3x.
C. y = −x4 + 2x2.
D. y = x4 − 2x2.
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
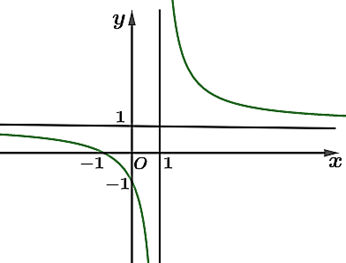
A. \(y = {x^3} - 3x - 1\).
B. \(y = \frac{{2x - 1}}{{x - 1}}\).
C. \(y = \frac{{x + 1}}{{x - 1}}\).
D. \(y = {x^4} + {x^2} + 1\).
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.\(y = \frac{{x + 2}}{{x - 1}}\).
B.\(y = - {x^3} + 3x + 1\).
C.\(y = - {x^4} + x + 1\).
D.\(y = {x^3} + 3x + 1\).
Tâm đối xứng của đồ thị hàm số \(y = {x^3} + 1\) là
A. \(C(1;\,\,2).\)
B. \(O(0\,;\,\,0).\)
C. \(A(0;\,\,1).\)
D. \(B(1;\,\,1).\)
Xác định tâm đối xứng của đồ thị hàm số sau
A. \(C(1;\,\,2).\)
B. \(O(0\,;\,\,0).\)
C. \(A(0;\,\,1).\)
D. \(B(1;\,\,1).\)
II. Thông hiểu
Cho hàm số y = f(x) = ax3 + bx2 + cx + d có bảng biến thiên sau:
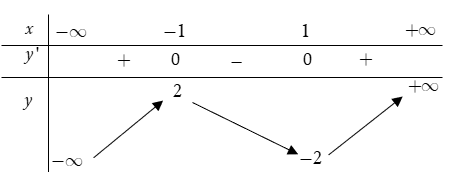
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số y = f(x)?
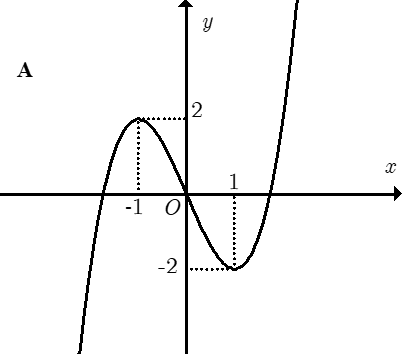
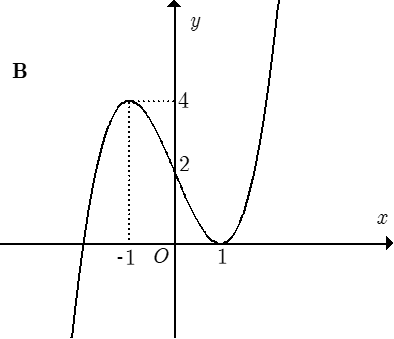
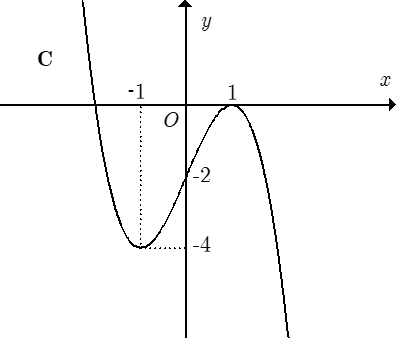
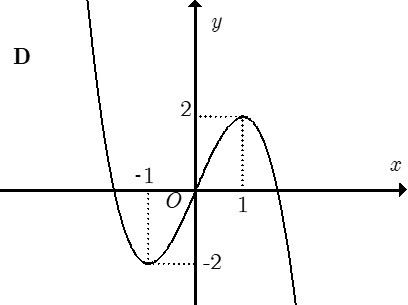
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
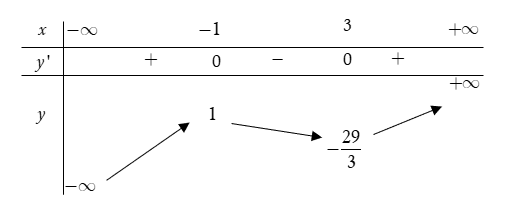
A. y = −x3 + 3x2 + 9x – 2.
B. \(y = \frac{1}{3}{x^3} - {x^2} - 3x - \frac{2}{3}\) .
C. y = x3 − 3x2 − 9x – 2.
D. \(y = - \frac{1}{3}{x^3} + {x^2} + 3x + \frac{2}{3}\).
Biết rằng hàm số y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là một trong các dạng dưới đây:
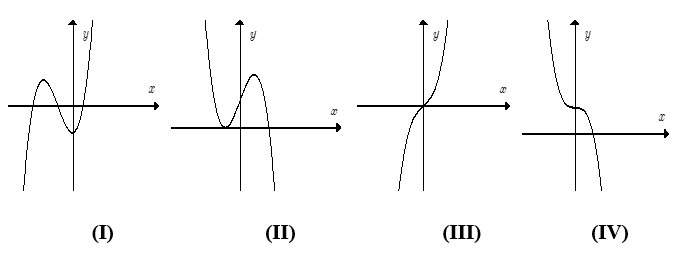
Mệnh đề nào sau đây là đúng?
A. Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.
B. Đồ thị (II) xảy ra khi a > 0 và f'(x) = 0 có hai nghiệm phân biệt.
C. Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm hoặc có nghiệm kép.
D. Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có có nghiệm kép.
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
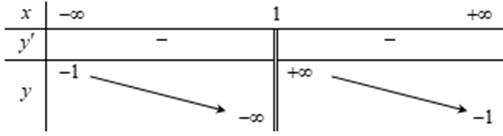
A.\(y = \frac{{x + 3}}{{x - 1}}\).
B.\(y = \frac{{ - x - 2}}{{x - 1}}\).
C.\(y = \frac{{ - x + 3}}{{x - 1}}\).
D.\(y = \frac{{ - x - 3}}{{x - 1}}\).
Hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) có bảng biến thiên nào dưới đây. Chọn đáp án đúng?
A.
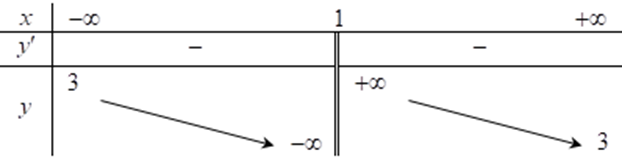
B.
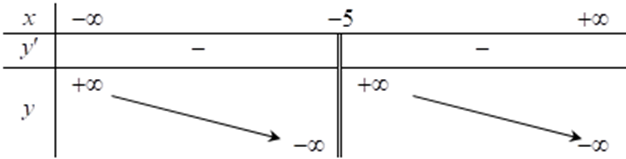
C.
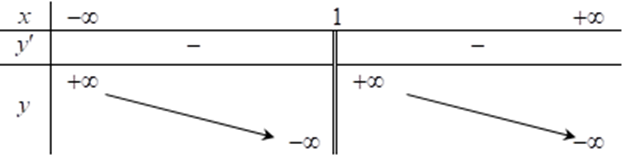
D.
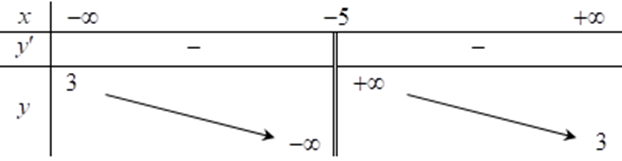
Cho hàm số \[y = \frac{{ax - b}}{{x - 1}}\] có đồ thị như hình vẽ dưới đây:
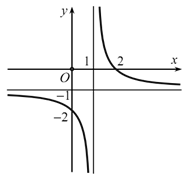
Khẳng định nào sau đây đúng?
A. \(b < a < 0\).
B. \(a < b < 0\).
C. \(b > a\)và \(a < 0\).
D. \(a < 0 < b\).
Bảng biến thiên sau là của hàm số nào?
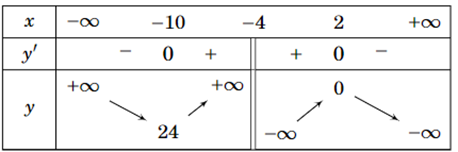
A. \(y = \frac{{{x^2} - 3x + 4}}{{ - x - 4}}\).
B. \(y = \frac{{{x^2} - 4x + 4}}{{ - x - 4}}\).
C. \(y = \frac{{{x^2} - 5x + 4}}{{x + 4}}\).
D. \(y = \frac{{{x^2} - 4x + 4}}{{x + 4}}\).
Bảng biến thiên sau là của đồ thị hàm số nào
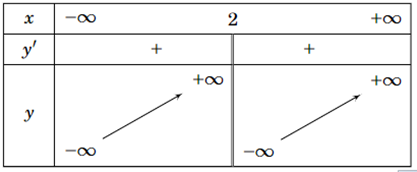
A. \(y = \frac{{{x^2} - 3}}{{x - 2}}\).
B. \(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
C. \(y = \frac{{{x^2} - x}}{{x - 2}}\).
D. \(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
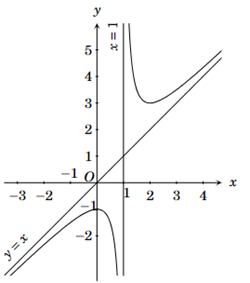
Đồ thị hàm số ở hình sau là của hàm số nào
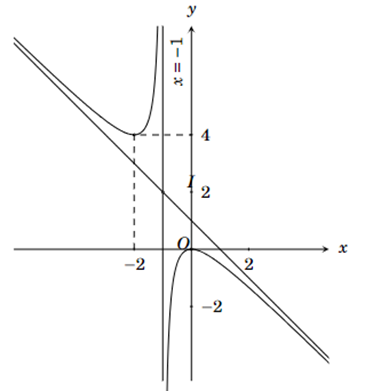
A. \(y = \frac{{{x^2} - x}}{{x + 1}}\).
B. \(y = \frac{{{x^2} - 3x}}{{x + 1}}\).
C. \(y = \frac{{{x^2} + x + 2}}{{x + 1}}\).
D. \(y = \frac{{ - {x^2}}}{{x + 1}}\).
Đồ thị hàm số ở hình sau là của hàm số nào.
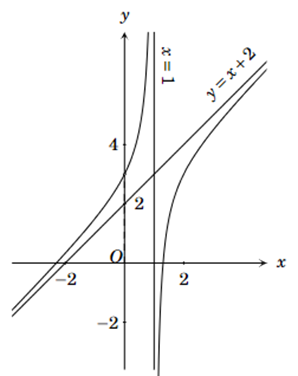
A. \(y = \frac{{{x^2} + 3}}{{x - 1}}\).
B. \(y = \frac{{{x^2} + x - 3}}{{x - 1}}\).
C. \(y = \frac{{{x^2} - 2x + 3}}{{ - x + 1}}\).
D. \(y = \frac{{{x^2} + 3}}{{ - x + 1}}\).
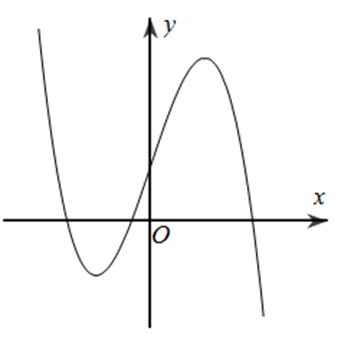
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên dưới.
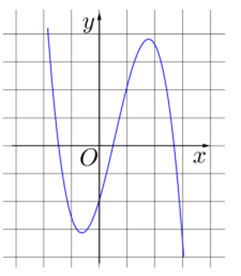
Mệnh đề nào dưới đây đúng?
A. a < 0, b > 0, c > 0, d < 0.
B. a < 0, b < 0, c > 0, d
C. a > 0, b < 0, c < 0, d > 0
D. a < 0, b > 0, c < 0, d < 0.
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như trong hình bên dưới. Biết rằng \[a\] là số thực dương, hỏi trong các số \[b,\,\,c,\,\,d\] có tất cả bao nhiêu số dương?
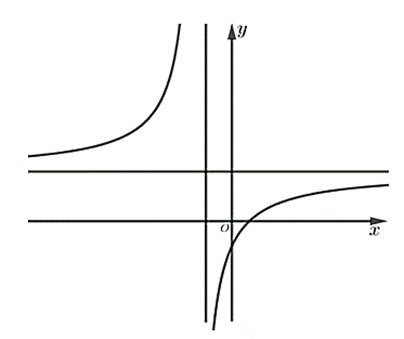
A. \[1\].
B. \[2\].
C. \[0\].
D. \[3\].
Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định được số lượng vi khuẩn tăng theo thời gian bởi qui luật \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con vi khuẩn), trong đó t là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào, số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu?
A. 0.
B. 1.
C. −10.
D. 10.
Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288\,\,\,d{m^3}\]. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,000\] đồng/\({m^2}\). Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
A. \[1,08\] triệu đồng.
B. \[0,91\] triệu đồng.
C. \[1,68\] triệu đồng.
D. \[0,54\] triệu đồng.
Một tấm kẽm hình vuông \(ABCD\) có cạnh bằng \(30{\rm{ (cm)}}{\rm{.}}\) Người ta gập tấm kẽm theo hai cạnh \[EF\] và \(GH\) cho đến khi \(AD\) và \(BC\) trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy. Giá trị của \(x\) để thể tích khối lăng trụ lớn nhất là
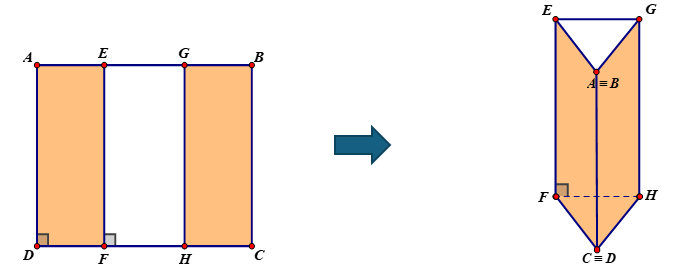
A. \(x = 5{\rm{ (cm)}}{\rm{.}}\)
B. \(x = 9{\rm{ (cm)}}{\rm{.}}\)
C. \(x = 8{\rm{ (cm)}}{\rm{.}}\)
D. \(x = 10{\rm{ (cm)}}{\rm{.}}\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải