20 câu trắc nghiệm Toán 10 Kết nối tri thức Bài 15: Hàm số (Đúng sai - Trả lời ngắn) có đáp án

Hàm số nào sau đây có tập xác định là ?

Với giá trị nào của thì hàm số xác định trên R.

Xét sự biến thiên của hàm số trên khoảng . Khẳng định nào sau đây đúng?

Cho hàm số . Điểm nào sau đây thuộc đồ thị hàm số đã cho?

Cho hàm số xác định trên khoảng có đồ thị như hình vẽ dưới đây.

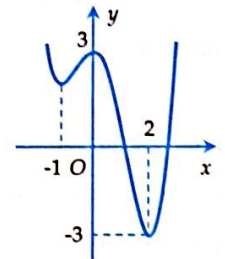
Mệnh đề nào sau đây đúng?

Cho hàm số 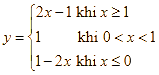. Giá trị lớn nhất của hàm số trên là:

Tìm giá trị nhỏ nhất của hàm số .

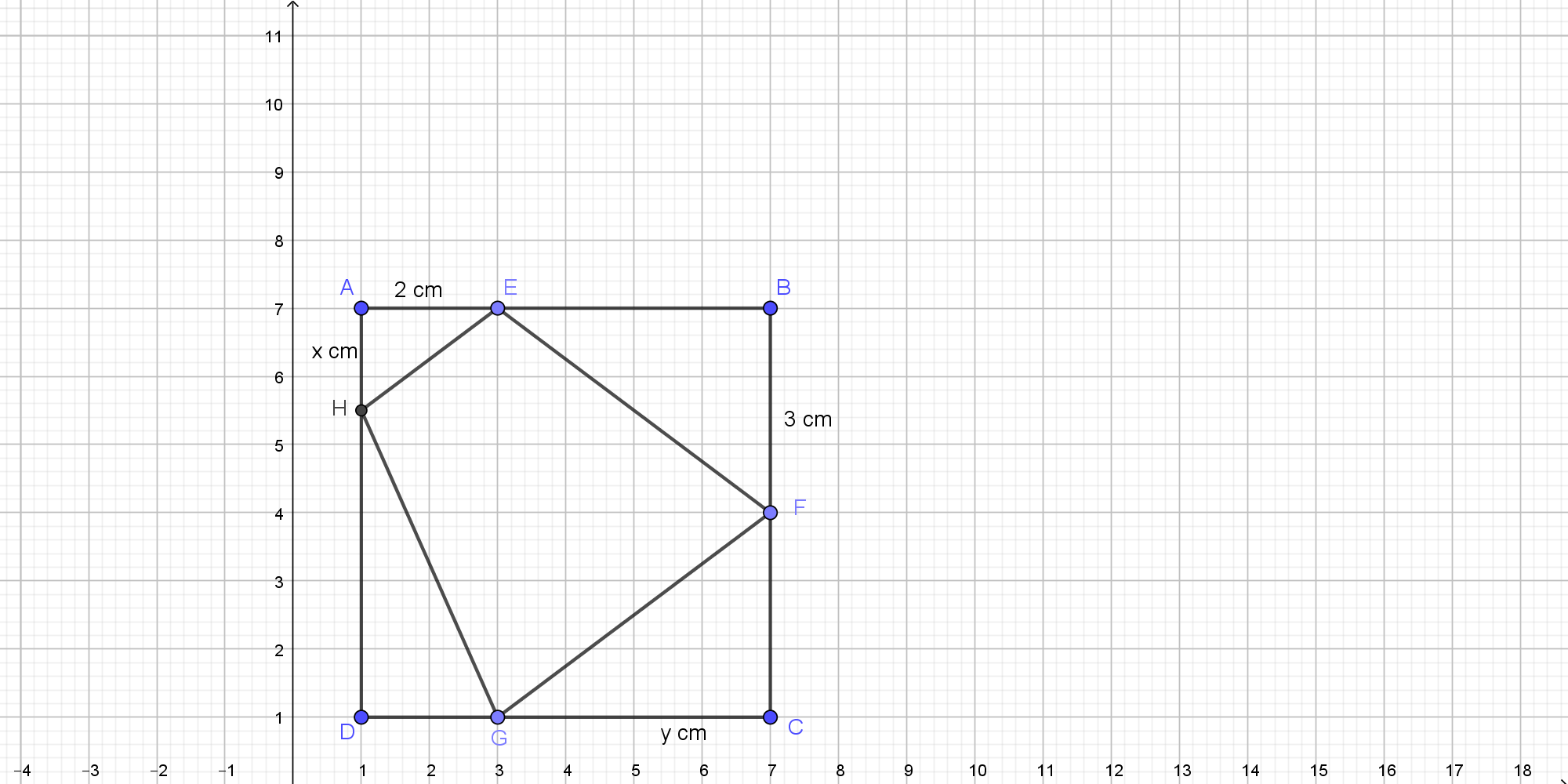
Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng để diện tích hình thang đạt giá trị nhỏ nhất.

Cho hàm số xác định trên R thỏa mãn 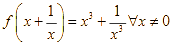. Tính .

a) Hàm số theo là .

b) Điều kiện của là .

c) Một khách hàng thuê một chiếc xe hơi công ty trong 7 ngày tết thì sẽ trả khoản tiền thuê là (đồng).

d) Anh Bình định dành ra một khoản tối đa là 10 triệu đồng cho phí thuê xe đi chơi trong dịp tết, khi đó anh Bình có thể thuê xe của công ty trên tối đa 12 ngày.

a) Tập xác định của hàm số là .

b) Tập giá trị của hàm số là .

c) Hàm số đồng biến trên tập xác định.

d) Trong khoảng thời gian từ 1989 đến 1999 dân số Việt Nam tăng nhanh nhất.

a) Hàm số có tập xác định là .

b) Điểm thuộc đồ thị hàm số.

c) .

d) Hàm số nghịch biến trên .

a) .

b) Hàm số có tập xác định là .

c) Biết , khi đó .

d) Với thì với .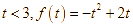

a) .

b) Tập xác định của hàm số là .

c) Hàm số đồng biến trong khoảng .

d) Tổng các hoành độ giao điểm của đồ thị hàm số và đường thẳng là .

Phần III. Trắc nghiệm trả lời ngắn

Cho hàm số 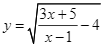. Biết rằng hàm số có tập xác định là . Tính tổng .

Cho hàm số ( là tham số thực) có đồ thị . Biết rằng đồ thị hàm số cắt hai trục tọa độ , tại hai điểm thỏa mãn , tính tổng tất các giá trị của tham số .

Cho hàm số sau: 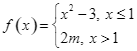. Tìm tham số m để .

Một nhân viên bán hàng sẽ nhận được một mức lương cơ bản là 6 triệu đồng mỗi tháng và một khoản hoa hồng là  nếu tổng doanh số trên 10 triệu đồng trong tháng. Ngoài ra, nếu doanh số bán hàng hàng tháng là 20 triệu đồng hoặc nhiều hơn thì nhân viên bán hàng nhận được thêm tiền thưởng là 600 nghìn đồng. Hỏi nhân viên đó sẽ nhận được bao nhiêu tiền lương nếu doanh số trong 1 tháng của nhân viên đó là 45 triệu đồng?

Biết rằng tồn tại  để hàm số nghịch biến trên khoảng . Gọi là giá trị nhỏ nhất của . Tính .