14 Bài tập Tìm tập xác định, tập giá trị của hàm số (có lời giải)
14 câu hỏi
Hàm số v = f(t) được cho bởi bảng như sau:

Tìm tập xác định của hàm số này.
Tìm tập giá trị của hàm số này.
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập xác định của hàm số.
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập giá trị của hàm số.
Tập xác định của hàm số f(x) = x – 2 là:
[2; +∞);
ℝ \ {2};
ℝ;
(–∞; 2].
Cho hàm số cho bởi bảng sau:
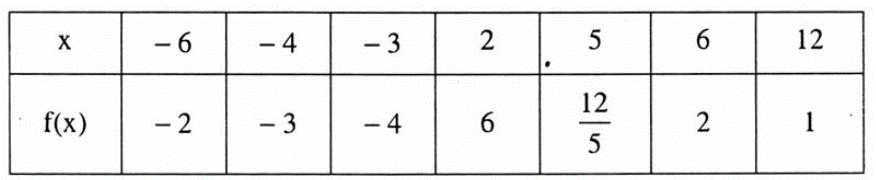
Tập xác định của hàm số f(x) là:
D = {–6; 4; 3; 2; 5; 6; 12};
D = {–6; –4; –3; 2; 5; 6; 12};
D = {–2; –3; –4; 6; 2,4; 2; 1};
D = ℝ.
Cho hàm số cho bởi bảng sau:
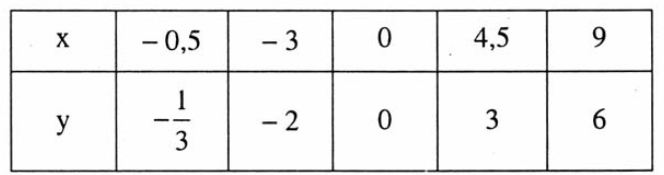
Tập xác định của hàm số y là:
D = {–0,5; –3; 0; 4,5; 9};
D = {–0,5; –3; 4,5; 9};
D = {–0,5; –3; 0; 4,5};
D = {–0,5; –3; 0; 4,5; 9; 1}.
Hàm số \(f(x) = \frac{1}{{x - 1}}\) có tập xác định là:
[1; +∞);
ℝ;
(–∞; 1];
ℝ \ {1}.
Tập xác định của hàm số \(f(x) = \frac{{x - 3}}{{x + 2}}\) là:
[–2; +∞);
ℝ \ {–2};
(–∞; –2];
ℝ.
Tập xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là:
[–1; +∞);
ℝ \ {–1};
(–∞; –1];
ℝ.
Tập xác định của hàm số \(f(x) = \sqrt {2x - 4} \) là:
[2; +∞);
ℝ \ {2};
(–∞; 2];
ℝ.
Hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) có tập xác định là:
[4; +∞);
ℝ \ {4};
(4; +∞);
ℝ.
Tập giá trị của hàm số: \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là:
[0; +∞);
ℝ \ {0};
(0; +∞);
ℝ.
Hàm số \(f(x) = \frac{{x - 4}}{{x + 4}}\) có tập giá trị là:
[0; +∞);
ℝ \ {0};
(0; +∞);
ℝ.





