110 CÂU HỎI
Đạo hàm của hàm số\(y = 10\)là:
A. \(10.\)
B. \( - 10.\)
C. \(0.\)
D. \(10x.\)
Cho hàm số \(f(x) = ax + b.\)Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(f'(x) = - a.\)
B. \(f'(x) = - b.\)
C. \(f'(x) = a.\)
D. \(f'(x) = b.\)
Cho 
và 
. Trong các mệnh đề sau, mệnh đề nào đúng?
A. 
B. 
C. 
D. không tồn tại.
Đạo hàm của hàm số \[y = {x^4} - 3{x^2} + x + 1\] là
A. \[y' = 4{x^3} - 6{x^2} + 1.\]
B. \[y' = 4{x^3} - 6{x^2} + x.\]
C. \[y' = 4{x^3} - 3{x^2} + x.\]
D. \[y' = 4{x^3} - 3{x^2} + 1.\]
Đạo hàm của hàm số 
bằng biểu thức nào sau đây?
A. 
B. 
C. 
D. 
\(y = {x^4} - 3{x^2} + 2x - 1\)
A. \(y' = 4{x^3} - 6x + 3\)
B. \(y' = 4{x^4} - 6x + 2\)
C. \(y' = 4{x^3} - 3x + 2\)
D. \(y' = 4{x^3} - 6x + 2\)
\(y = - \frac{{{x^3}}}{3} + 2{x^2} + x - 1\)
A. \(y' = - 2{x^2} + 4x + 1\)
B. \(y' = - 3{x^2} + 4x + 1\)
C. \(y' = - \frac{1}{3}{x^2} + 4x + 1\)
D. \(y' = - {x^2} + 4x + 1\)
Đạo hàm cấp một của hàm số \(y = {\left( {1 - {x^3}} \right)^5}\) là:
A. \(y' = 5{\left( {1 - {x^3}} \right)^4}\).
B. \(y' = - 15{x^2}{\left( {1 - {x^3}} \right)^5}\).
C. \(y' = - 3{\left( {1 - {x^3}} \right)^4}\).
D. \(y' = - 5{x^2}{\left( {1 - {x^3}} \right)^4}\).
Cho hàm số\[f\left( x \right)\]xác định trên \[\mathbb{R}\] bởi\[f\left( x \right) = ax + b\], với \[a,\]\[b\] là hai số thực đã cho. Chọn câu đúng:
A. \[f'\left( x \right) = a\].
B. \[f'\left( x \right) = - a\].
C. \[f'\left( x \right) = b\].
D. \[f'\left( x \right) = - b\].
Cho hàm số \[f\left( x \right)\]xác định trên \[\mathbb{R}\] bởi \[f\left( x \right) = - 2{x^2} + 3x\]. Hàm số có đạo hàm \[f'\left( x \right)\] bằng:
A. \[ - 4x - 3\].
B. \[ - 4x + 3\].
C. \[4x + 3\].
D. \[4x - 3\].
Đạo hàm của \[y = {\left( {{x^5} - 2{x^2}} \right)^2}\] là
A. \[y' = 10{x^9} - 28{x^6} + 16{x^3}.\]
B. \[y' = 10{x^9} - 14{x^6} + 16{x^3}.\]
C. \[y' = 10{x^9} + 16{x^3}.\]
D. \[y' = 7{x^6} - 6{x^3} + 16x.\]
Đạo hàm của hàm số \(y = {(7x - 5)^4}\) bằng biểu thức nào sau đây
A. \(4{(7x - 5)^3}.\)
B. \( - 28{(7x - 5)^3}.\)
C. \(28{(7x - 5)^3}.\)
D. \[A = y'' + y = - 3\sin x - 2\cos x + 3\sin x + 2{\rm{cos}}x = 0\]
Cho hàm số \[f\left( x \right) = - 2{x^2} + 3x\]. Hàm số có đạo hàm \(f'\left( x \right)\) bằng
A. \[4x - 3.\]
B. \[ - 4x + 3.\]
C. \[4x + 3.\]
D. \[ - 4x - 3.\]
Đạo hàm của hàm số \[y = {({x^3} - 2{x^2})^2}^{016}\]là:
A. \[y' = 2016{({x^3} - 2{x^2})^2}^{015}.\]
B. \[y' = 2016{({x^3} - 2{x^2})^{2015}}(3{x^2} - 4x).\]
C. \[y' = 2016({x^3} - 2{x^2})(3{x^2} - 4x).\]
D. \[y' = 2016({x^3} - 2{x^2})(3{x^2} - 2x).\]
Đạo hàm của \[y = {\left( {{x^3} - 2{x^2}} \right)^2}\]bằng :
A. \[6{x^5} - 20{x^4} + 16{x^3}\].
B. \[6{x^5} + 16{x^3}\].
C. \[6{x^5} - 20{x^4} + 4{x^3}\].
D. \[6{x^5} - 20{x^4} - 16{x^3}\].
Đạo hàm của hàm số\[y = \frac{1}{2}{x^6} - \frac{3}{x} + 2\sqrt x \] là:
A. \[y' = 3{x^5} + \frac{3}{{{x^2}}} + \frac{1}{{\sqrt x }}.\]
B. \[y' = 6{x^5} + \frac{3}{{{x^2}}} + \frac{1}{{2\sqrt x }}.\]
C. \[y' = 3{x^5} - \frac{3}{{{x^2}}} + \frac{1}{{\sqrt x }}.\]
D. \[y' = 6{x^5} - \frac{3}{{{x^2}}} + \frac{1}{{2\sqrt x }}.\]
Đạo hàm của hàm số \[y = {\left( {3{x^2} - 1} \right)^2}\]là \[y'\] bằng.
A. \[2\left( {3{x^2} - 1} \right)\].
B. \[6\left( {3{x^2} - 1} \right)\].
C. \[6x\left( {3{x^2} - 1} \right)\].
D. \[12x\left( {3{x^2} - 1} \right)\].
Đạo hàm của hàm số 
là:
A. 
B. 
C. 
D. 
Tính đạo hàm của hàm số\(y = {\left( {{x^7} + x} \right)^2}\,\)
A. \(y' = ({x^7} + x)(7{x^6} + 1)\)
B. \(y' = 2({x^7} + x)\)
C. \(y' = 2(7{x^6} + 1)\)
D. \(y' = 2({x^7} + x)(7{x^6} + 1)\)
Tính đạo hàm của hàm số\(y = \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)\)
A. \(y' = - {x^3} + 4x\)
B. \(y' = - {x^3} - 4x\)
C. \(y' = 12{x^3} + 4x\)
D. \(y' = - 12{x^3} + 4x\)
Tính đạo hàm của hàm số\(y = {({x^3} + 2x)^3}\)
A. \(y' = {({x^3} + 2x)^2}(3{x^2} + 2)\)
B. \(y' = 2{({x^3} + 2x)^2}(3{x^2} + 2)\)
C. \(y' = 3{({x^3} + 2x)^2} + (3{x^2} + 2)\)
D. \(y' = 3{({x^3} + 2x)^2}(3{x^2} + 2)\)
Tính đạo hàm của hàm số\(y = ({x^2} - 1)(3{x^3} + 2x)\)
A. \(y' = {x^4} - 3{x^2} - 2\)
B. \(y' = 5{x^4} - 3{x^2} - 2\)
C. \(y' = 15{x^4} - 3{x^2}\)
D. \(y' = 15{x^4} - 3{x^2} - 2\)
Tính đạo hàm của hàm số\(y = {x^2}\left( {2x + 1} \right)\left( {5x - 3} \right)\)
A. \(y' = 40{x^2} - 3{x^2} - 6x\)
B. \(y' = 40{x^3} - 3{x^2} - 6x\)
C. \(y' = 40{x^3} + 3{x^2} - 6x\)
D. \(y' = 40{x^3} - 3{x^2} - x\)
Tính đạo hàm của hàm số\(y = {(x + 2)^3}{(x + 3)^2}\)
A. \(y' = 3{({x^2} + 5x + 6)^3} + 2(x + 3){(x + 2)^3}\)
B. \(y' = 2{({x^2} + 5x + 6)^2} + 3(x + 3){(x + 2)^3}\)
C. \(y' = 3({x^2} + 5x + 6) + 2(x + 3)(x + 2)\)
D. \(y' = 3{({x^2} + 5x + 6)^2} + 2(x + 3){(x + 2)^3}\)
Tính đạo hàm của hàm số sau: \(y = {\left( {{x^7} + x} \right)^2}\).
A. \(\left( {{x^7} + x} \right)\left( {7{x^6} + 1} \right)\)
B. \(2\left( {7{x^6} + 1} \right)\)
C. \(2\left( {{x^7} + x} \right)\left( {{x^6} + 1} \right)\)
D. \(2\left( {{x^7} + x} \right)\left( {7{x^6} + 1} \right)\)
Tính đạo hàm của hàm số sau: \(y = {\left( {2{x^3} - 3{x^2} - 6x + 1} \right)^2}\).
A. \(2\left( {2{x^3} - {x^2} + 6x + 1} \right)\left( {6{x^2} - 6x + 6} \right).\)
B. \(2\left( {2{x^3} - 3{x^2} + x + 1} \right)\left( {{x^2} - 6x + 6} \right).\)
C. \(2\left( {2{x^3} - 3{x^2} + 6x + 1} \right)\left( {{x^2} - 6x + 6} \right).\)
D. \(2\left( {2{x^3} - 3{x^2} + 6x + 1} \right)\left( {6{x^2} - 6x + 6} \right).\)
Tính đạo hàm của hàm số sau: \(y = {\left( {1 - 2{x^2}} \right)^3}.\)
A. \(12x{\left( {1 - 2{x^2}} \right)^2}.\)
B. \( - 12x{\left( {1 - 2{x^2}} \right)^2}.\)
C. \( - 24x{\left( {1 - 2{x^2}} \right)^2}.\)
D. \(24x{\left( {1 - 2{x^2}} \right)^2}.\)
Tính đạo hàm của hàm số sau: \(y = {\left( {x - {x^2}} \right)^{32}}\).
A. \({\left( {x - {x^2}} \right)^{31}}.\left( {1 - 2x} \right)\)
B. \(32{\left( {x - {x^2}} \right)^{31}}\)
C. \(32{\left( {1 - {x^2}} \right)^{31}}\)
D. \(32{\left( {x - {x^2}} \right)^{31}}.\left( {1 - 2x} \right)\)
Tính đạo hàm của hàm số sau: \(y = {\left( {{x^2} + x + 1} \right)^4}\).
A. \(4{\left( {{x^2} + x + 1} \right)^3}.\)
B. \({\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
C. \({\left( {{x^2} + x + 1} \right)^3}.\)
D. \(4{\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
Tính đạo hàm của hàm số sau: \(y = {\left( {{x^2} - x + 1} \right)^3}.{\left( {{x^2} + x + 1} \right)^2}\)
A. \(y' = {\left( {{x^2} - x + 1} \right)^2}\left[ {3\left( {2x - 1} \right)\left( {{x^2} + x + 1} \right) + 2\left( {2x + 1} \right)\left( {{x^2} - x + 1} \right)} \right]\)
B. \(y' = {\left( {{x^2} - x + 1} \right)^2}\left( {{x^2} + x + 1} \right)\left[ {3\left( {2x - 1} \right)\left( {{x^2} + x + 1} \right) + \left( {{x^2} - x + 1} \right)} \right]\)
C. \(y' = {\left( {{x^2} - x + 1} \right)^2}\left( {{x^2} + x + 1} \right)\left[ {3\left( {2x - 1} \right)\left( {{x^2} + x + 1} \right) + 2\left( {2x + 1} \right)\left( {{x^2} - x + 1} \right)} \right]\)
D. \(y' = {\left( {{x^2} - x + 1} \right)^2}\left( {{x^2} + x + 1} \right)\left[ {3\left( {2x - 1} \right)\left( {{x^2} + x + 1} \right) - 2\left( {2x + 1} \right)\left( {{x^2} - x + 1} \right)} \right]\)
Tính đạo hàm của hàm số sau: \(y = \left( {1 + 2x} \right)\left( {2 + 3{x^2}} \right)\left( {3 - 4{x^3}} \right)\)
A. \(y' = \left( {2 + 3{x^2}} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {6x} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {2 + 3{x^2}} \right)\left( { - 12{x^2}} \right)\)
B. \(y' = 4\left( {2 + 3{x^2}} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {6x} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {2 + 3{x^2}} \right)\left( { - 12{x^2}} \right)\)
C. \(y' = 2\left( {2 + 3{x^2}} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {6x} \right)\left( {3 - 4{x^3}} \right) + \left( {1 - 2x} \right)\left( {2 + 3{x^2}} \right)\left( { - 12{x^2}} \right)\)
D. \(y' = 2\left( {2 + 3{x^2}} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {6x} \right)\left( {3 - 4{x^3}} \right) + \left( {1 + 2x} \right)\left( {2 + 3{x^2}} \right)\left( { - 12{x^2}} \right)\)
Tính đạo hàm của hàm số sau: \(y = \frac{{ax + b}}{{cx + d}}{\rm{, }}ac \ne 0\)
A. \(\frac{a}{c}\)
B. \(\frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
C. \(\frac{{ad + bc}}{{{{\left( {cx + d} \right)}^2}}}\)
D. \(\frac{{ad - bc}}{{\left( {cx + d} \right)}}\)
Tính đạo hàm của hàm số sau: \(y = \frac{{2x + 1}}{{x + 2}}\)
A. \( - \frac{3}{{{{\left( {x + 2} \right)}^2}}}\)
B. \(\frac{3}{{\left( {x + 2} \right)}}\)
C. \(\frac{3}{{{{\left( {x + 2} \right)}^2}}}\)
D. \(\frac{2}{{{{\left( {x + 2} \right)}^2}}}\)
Cho hàm số \(y = \frac{{3x + 5}}{{ - 1 + 2x}}\). Đạo hàm \[y'\]của hàm số là:
A. \(\frac{7}{{{{(2x - 1)}^2}}}\).
B. \(\frac{1}{{{{(2x - 1)}^2}}}\).
C. \( - \frac{{13}}{{{{(2x - 1)}^2}}}\).
D. \(\frac{{13}}{{{{(2x - 1)}^2}}}\).
Cho hàm số \[f\left( x \right) = \frac{{2x - 1}}{{x + 1}}\] xác định . Đạo hàm của hàm số \[f\left( x \right)\]là:
A. \(f'\left( x \right) = \frac{2}{{{{\left( {x + 1} \right)}^2}}}\).
B. \[f'\left( x \right) = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\].
C. \(f'\left( x \right) = \frac{1}{{{{\left( {x + 1} \right)}^2}}}\).
D. \(f'\left( x \right) = \frac{{ - 1}}{{{{\left( {x + 1} \right)}^2}}}\).
Hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) có đạo hàm là:
A. \(y' = 2\).
B. \(y' = - \frac{1}{{{{\left( {x - 1} \right)}^2}}}\).
C. \(y' = - \frac{3}{{{{\left( {x - 1} \right)}^2}}}\).
D. \(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\).
Cho hàm số 
. Đạo hàm 
của hàm số là
A. 
B. 
C. 
D. 
Đạo hàm của hàm số 
là:
A. 
B. 
C. 
D. 
Cho hàm số 
. Hàm số có đạo hàm 
bằng:
A. 
.
B. 
.
C. 
.
D. 
.
Tính đạo hàm của hàm số sau: \(y = \frac{3}{{{{(2x + 5)}^2}}}\)
A. \( - \frac{{12}}{{{{\left( {2x + 5} \right)}^4}}}\)
B. \(\frac{{12}}{{{{\left( {2x + 5} \right)}^3}}}\)
C. \( - \frac{6}{{{{\left( {2x + 5} \right)}^3}}}\)
D. \( - \frac{{12}}{{{{\left( {2x + 5} \right)}^3}}}\)
Tính đạo hàm của hàm số sau: \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)
A. \(\frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\)
B. \(\frac{{{x^2} + 2x}}{{{{\left( {x - 1} \right)}^2}}}\)
C. \(\frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\)
D. \(\frac{{ - 2x - 2}}{{{{\left( {x - 1} \right)}^2}}}\)
Tính đạo hàm của hàm số sau: \(y = \frac{{a{x^2} + bx + c}}{{a'x + b'}},{\rm{ }}aa' \ne 0\).
A. \( = \frac{{aa'{x^2} + 2ab'x + bb' - a'c}}{{(a'x + b')}}\)
B. \( = \frac{{aa'{x^2} + 2ab'x + bb' - a'c}}{{{{(a'x + b')}^2}}}\)
C. \( = \frac{{aa'{x^2} - 2ab'x + bb' - a'c}}{{{{(a'x + b')}^2}}}\)
D. \( = \frac{{aa'{x^2} + 2ab'x - bb' - a'c}}{{{{(a'x + b')}^2}}}\)
Tính đạo hàm của hàm số sau: \(y = \frac{{2 - 2x + {x^2}}}{{{x^2} - 1}}\)
A. \(\frac{{2{x^2} + 6x + 2}}{{{{\left( {{x^2} - 1} \right)}^2}}}\)
B. \(\frac{{2{x^2} - 6x + 2}}{{{{\left( {{x^2} - 1} \right)}^4}}}\)
C. \(\frac{{2{x^2} - 6x - 2}}{{{{\left( {{x^2} - 1} \right)}^2}}}\)
D. \(\frac{{2{x^2} - 6x + 2}}{{{{\left( {{x^2} - 1} \right)}^2}}}\)
Cho hàm số 
. Đạo hàm y' của hàm số là
A. 
B. 
C. 
D. 
Hàm số 
có y' bằng
A. 
B. 
C. 
D. 
Hàm số \(y = \frac{{{{\left( {x - 2} \right)}^2}}}{{1 - x}}\) có đạo hàm là:
A. \(y' = \frac{{ - {x^2} + 2x}}{{{{\left( {1 - x} \right)}^2}}}\).
B. \(y' = \frac{{{x^2} - 2x}}{{{{\left( {1 - x} \right)}^2}}}\).
C. \(y' = - 2\left( {x - 2} \right)\).
D. \(y' = \frac{{{x^2} + 2x}}{{{{\left( {1 - x} \right)}^2}}}\).
Cho hàm số \(y = \frac{{ - {x^2} + 2x - 3}}{{x - 2}}\). Đạo hàm \[y'\] của hàm số là biểu thức nào sau đây?
A. \( - 1 - \frac{3}{{{{(x - 2)}^2}}}\).
B. \(1 + \frac{3}{{{{(x - 2)}^2}}}\).
C. \( - 1 + \frac{3}{{{{(x - 2)}^2}}}\).
D. \(1 - \frac{3}{{{{(x - 2)}^2}}}\).
Cho hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x + 2}}\). Đạo hàm \({y^\prime }\)của hàm số là
A. 1+ \(\frac{3}{{{{(x + 2)}^2}}}\).
B. \(\frac{{{x^2} + 6x + 7}}{{{{(x + 2)}^2}}}\).
C. \(\frac{{{x^2} + 4x + 5}}{{{{(x + 2)}^2}}}\).
D. \(\frac{{{x^2} + 8x + 1}}{{{{(x + 2)}^2}}}\).
Đạo hàm của hàm số \(y = \frac{1}{{{x^2} - 2x + 5}}\) bằng biểu thức nào sau đây
A. \[y' = \frac{{2x - 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.\]
B. \[y' = \frac{{ - 2x + 2}}{{{{\left( {{x^2} - 2x + 5} \right)}^2}}}.\]
C. \(y' = (2x - 2)({x^2} - 2x + 5).\)
D. \(y' = \frac{1}{{2x - 2}}.\)
Đạo hàm của \[y = \frac{1}{{2{x^2} + x + 1}}\] bằng :
A. \[\frac{{ - \left( {4x + 1} \right)}}{{{{\left( {2{x^2} + x + 1} \right)}^2}}}.\]
B. \[\frac{{ - \left( {4x - 1} \right)}}{{{{\left( {2{x^2} + x + 1} \right)}^2}}}.\]
C. \[\frac{{ - 1}}{{{{\left( {2{x^2} + x + 1} \right)}^2}}}.\]
D. \[\frac{{\left( {4x + 1} \right)}}{{{{\left( {2{x^2} + x + 1} \right)}^2}}}.\]
Cho hàm số \[f\left( x \right) = x + 1 - \frac{2}{{x - 1}}\]. Xét hai câu sau:
(I) \[f'\left( x \right) = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\,\,\forall x \ne 1\] (II) \(f'\left( x \right) > 0\,\,\forall x \ne 1.\)
Hãy chọn câu đúng:
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả hai đều sai.
D. Cả hai đều đúng.
Cho hàm số \[f(x) = \frac{{{x^2} + x - 1}}{{x - 1}}\]. Xét hai câu sau:
\[(I):f'(x) = 1 - \frac{1}{{{{(x - 1)}^2}}},\]\[\forall x \ne 1.\] \[(II):f'(x) = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}},\]\[\forall x \ne 1.\]
Hãy chọn câu đúng:
A. Chỉ \[(I)\]đúng.
B. Chỉ \[(II)\]đúng.
C. Cả \[(I);\]\[(II)\]đều sai.
D. Cả \[(I);\]\[(II)\]đều đúng.
Đạo hàm của hàm số \(y = \frac{{x(1 - 3x)}}{{x + 1}}\) bằng biểu thức nào sau đây?
A. \(\frac{{ - 9{x^2} - 4x + 1}}{{{{(x + 1)}^2}}}.\)
B. \(\frac{{ - 3{x^2} - 6x + 1}}{{{{(x + 1)}^2}}}.\)
C. \(1 - 6{x^2}.\)
D. \(\frac{{1 - 6{x^2}}}{{{{(x + 1)}^2}}}.\)
Cho hàm số\(y = \frac{{ - 2{x^2} + x - 7}}{{{x^2} + 3}}\). Đạo hàm\(y'\)của hàm số là:
A. \(\frac{{ - 3{x^2} - 13x - 10}}{{{{({x^2} + 3)}^2}}}.\)
B. \(\frac{{ - {x^2} + x + 3}}{{{{({x^2} + 3)}^2}}}.\)
C. \(\frac{{ - {x^2} + 2x + 3}}{{{{({x^2} + 3)}^2}}}.\)
D. \(\frac{{ - 7{x^2} - 13x - 10}}{{{{({x^2} + 3)}^2}}}.\)
Cho hàm số \(y = \frac{{2x + 5}}{{{x^2} + 3x + 3}}\). Đạo hàm \[y'\]của hàm số là:
A. \(\frac{{2{x^2} + 10x + 9}}{{{{({x^2} + 3x + 3)}^2}}}\).
B. \(\frac{{ - 2{x^2} - 10x - 9}}{{{{({x^2} + 3x + 3)}^2}}}\).
C. \(\frac{{{x^2} - 2x - 9}}{{{{({x^2} + 3x + 3)}^2}}}\).
D. \(\frac{{ - 2{x^2} - 5x - 9}}{{{{({x^2} + 3x + 3)}^2}}}\).
Đạo hàm của hàm số \(y = \frac{1}{{{x^2} - 2x + 5}}\) bằng biểu thức nào sau đây?
A. \(\frac{{ - 2x - 2}}{{{{({x^2} - 2x + 5)}^2}}}.\)
B. \(\frac{{ - 4x + 4}}{{{{({x^2} - 2x + 5)}^2}}}.\)
C. \(\frac{{ - 2x + 2}}{{{{({x^2} - 2x + 5)}^2}}}.\)
D. \(\frac{{2x + 2}}{{{{({x^2} - 2x + 5)}^2}}}.\)
Hàm số \[y = 2x + 1 + \frac{2}{{x - 2}}\]có \(y'\) bằng?
A. \[\frac{{2{x^2} + 8x + 6}}{{{{(x - 2)}^2}}}\].
B. \[\frac{{2{x^2} - 8x + 6}}{{x - 2}}.\]
C. \[\frac{{2{x^2} - 8x + 6}}{{{{(x - 2)}^2}}}\].
D. \[\frac{{2{x^2} + 8x + 6}}{{x - 2}}\].
Đạo hàm của hàm số \(y = \frac{1}{{(x - 1)(x + 3)}}\) bằng biểu thức nào sau đây ?.
A. \(\frac{1}{{{{(x + 3)}^2}{{(x - 1)}^2}}}\).
B. \(\frac{1}{{2x + 2}}\).
C. \( - \frac{{2x + 2}}{{{{({x^2} + 2x - 3)}^2}}}\).
D. \(\frac{{ - 4}}{{{{\left( {{x^2} + 2x - 3} \right)}^2}}}\).
Cho hàm số \(y = \frac{{2{x^2} + 3x - 1}}{{{x^2} - 5x + 2}}.\) Đạo hàm \[y'\] của hàm số là.
A. \(\frac{{ - 13{x^2} - 10x + 1}}{{{{({x^2} - 5x + 2)}^2}}}\).
B. \(\frac{{ - 13{x^2} + 5x + 11}}{{{{({x^2} - 5x + 2)}^2}}}\).
C. \(\frac{{ - 13{x^2} + 5x + 1}}{{{{({x^2} - 5x + 2)}^2}}}.\)
D. \(\frac{{ - 13{x^2} + 10x + 1}}{{{{({x^2} - 5x + 2)}^2}}}.\)
Hàm số nào sau đây có \[y' = 2x + \frac{1}{{{x^2}}}\]
A. \[y = {x^2} - \frac{1}{x}.\]
B. \[y = 2 - \frac{2}{{{x^3}}}.\]
C. \[y = {x^2} + \frac{1}{x}.\]
D. \[y = 2 - \frac{1}{x}.\]
Đạo hàm của hàm số \(y = \frac{1}{{{x^3}}} - \frac{1}{{{x^2}}}\) bằng biểu thức nào sau đây?
A. \(\frac{{ - 3}}{{{x^4}}} + \frac{1}{{{x^3}}}.\)
B. \(\frac{{ - 3}}{{{x^4}}} + \frac{2}{{{x^3}}}.\)
C. \(\frac{{ - 3}}{{{x^4}}} - \frac{2}{{{x^3}}}.\)
D. \(\frac{3}{{{x^4}}} - \frac{1}{{{x^3}}}.\)
Hàm số nào sau đây có \[y' = 2x + \frac{1}{{{x^2}}}\]?
A. \[y = \frac{{{x^3} - 1}}{x}\]
B. \[y = \frac{{3({x^2} + x)}}{{{x^3}}}\]
C. \[y = \frac{{{x^3} + 5x - 1}}{x}\]
D. \[y = \frac{{2{x^2} + x - 1}}{x}\]
Tính đạo hàm của hàm số \(y = {\left( {x + \frac{2}{{3{x^2}}}} \right)^2}\)
A. \(y' = \left( {x + \frac{2}{{3{x^2}}}} \right)\left( {1 - \frac{4}{{3{x^3}}}} \right)\)
B. \(y' = 2\left( {x + \frac{2}{{3{x^2}}}} \right)\left( {1 + \frac{4}{{3{x^3}}}} \right)\)
C. \(y' = \left( {x + \frac{2}{{3{x^2}}}} \right)\left( {1 + \frac{4}{{3{x^3}}}} \right)\)
D. \(y' = 2\left( {x + \frac{2}{{3{x^2}}}} \right)\left( {1 - \frac{4}{{3{x^3}}}} \right)\)
Tính đạo hàm của hàm số\(y = {\left( {4x + \frac{5}{{{x^2}}}} \right)^3}\)
A. \(y' = 3\left( {4 + \frac{{10}}{{{x^3}}}} \right){\left( {4x + \frac{5}{{{x^2}}}} \right)^2}\)
B. \(y' = 3\left( {4 - \frac{{10}}{{{x^3}}}} \right){\left( {4x - \frac{5}{{{x^2}}}} \right)^2}\)
C. \(y' = {\left( {4x + \frac{5}{{{x^2}}}} \right)^2}\)
D. \(y' = 3\left( {4 - \frac{{10}}{{{x^3}}}} \right){\left( {4x + \frac{5}{{{x^2}}}} \right)^2}\)
Cho hàm số 
. Đạo hàm y' của hàm số là
A. 
B. 
C. 
D. 
Tính đạo hàm của hàm số\(y = \sqrt {{x^3} - 3{x^2} + 2} \)
A. \(y' = \frac{{3{x^2} - 6x}}{{\sqrt {{x^3} - 3{x^2} + 2} }}\)
B. \(y' = \frac{{3{x^2} + 6x}}{{2\sqrt {{x^3} - 3{x^2} + 2} }}\)
C. \(y' = \frac{{3{x^2} - 6x}}{{2\sqrt {{x^3} - 3{x^2} - 2} }}\)
D. \(y' = \frac{{3{x^2} - 6x}}{{2\sqrt {{x^3} - 3{x^2} + 2} }}\)
Đạo hàm của hàm số 
là kết quả nào sau đây?
A. 
B. 
C. 
D. 
Cho hàm số \[f\left( x \right) = x\sqrt x \] có đạo hàm \[f'\left( x \right)\]bằng.
A. \[\frac{{3\sqrt x }}{2}\].
B. \[\frac{{\sqrt x }}{{2x}}\].
C. \[\sqrt x + \frac{{\sqrt x }}{2}\].
D. \[\frac{{\sqrt x }}{2}\].
Đạo hàm của hàm số \(y = \left( {{x^3} - 5} \right).\sqrt x \) bằng biểu thức nào sau đây?
A. \(\frac{7}{2}\sqrt {{x^5}} - \frac{5}{{2\sqrt x }}.\)
B. \(3{x^2} - \frac{1}{{2\sqrt x }}.\)
C. \(3{x^2} - \frac{5}{{2\sqrt x }}.\)
D. \(\frac{7}{2}\sqrt[5]{{{x^2}}} - \frac{5}{{2\sqrt x }}.\)
Đạo hàm của hàm số\[y = \sqrt {{x^2} - 4{x^3}} \] là :
A. \[\frac{{x - 6{x^2}}}{{\sqrt {{x^2} - 4{x^3}} }}.\]
B. \[\frac{1}{{2\sqrt {{x^2} - 4{x^3}} }}.\]
C. \[\frac{{x - 12{x^2}}}{{2\sqrt {{x^2} - 4{x^3}} }}.\]
D. \[\frac{{x - 6{x^2}}}{{2\sqrt {{x^2} - 4{x^3}} }}.\]
Đạo hàm của \[y = \sqrt {3{x^2} - 2x + 1} \]bằng:
A. \[\frac{{3x - 1}}{{\sqrt {3{x^2} - 2x + 1} }}.\]
B. \[\frac{{6x - 2}}{{\sqrt {3{x^2} - 2x + 1} }}.\]
C. \[\frac{{3{x^2} - 1}}{{\sqrt {3{x^2} - 2x + 1} }}.\]
D. \[\frac{1}{{2\sqrt {3{x^2} - 2x + 1} }}.\]
Cho hàm số\(y = \sqrt {2{x^2} + 5x - 4} \). Đạo hàm\(y'\)của hàm số là:
A. \(\frac{{4x + 5}}{{2\sqrt {2{x^2} + 5x - 4} }}.\)
B. \(\frac{{4x + 5}}{{\sqrt {2{x^2} + 5x - 4} }}.\)
C. \(\frac{{2x + 5}}{{2\sqrt {2{x^2} + 5x - 4} }}.\)
D. \(\frac{{2x + 5}}{{\sqrt {2{x^2} + 5x - 4} }}.\)
Tính đạo hàm các hàm số sau \(y = x\sqrt {{x^2} + 1} \)
A. \(\frac{{2{x^2} + 1}}{{2\sqrt {{x^2} + 1} }}\)
B. \(\frac{{{x^2} + 1}}{{\sqrt {{x^2} + 1} }}\)
C. \(\frac{{4{x^2} + 1}}{{\sqrt {{x^2} + 1} }}\)
D. \(\frac{{2{x^2} + 1}}{{\sqrt {{x^2} + 1} }}\)
Đạo hàm của hàm số\[y = x.\sqrt {{x^2} - 2x} \]là
A. \[y' = \frac{{2x - 2}}{{\sqrt {{x^2} - 2x} }}.\]
B. \[y' = \frac{{3{x^2} - 4x}}{{\sqrt {{x^2} - 2x} }}.\]
C. \[y' = \frac{{2{x^2} - 3x}}{{\sqrt {{x^2} - 2x} }}.\]
D. \[y' = \frac{{2{x^2} - 2x - 1}}{{\sqrt {{x^2} - 2x} }}.\]
Cho hàm số \[f\left( x \right)\]xác định trên \[D = \left[ {0; + \infty } \right)\] cho bởi \[f\left( x \right) = x\sqrt x \] có đạo hàm là:
A. \[f'\left( x \right) = \frac{1}{2}\sqrt x \].
B. \[f'\left( x \right) = \frac{3}{2}\sqrt x \].
C. \[f'\left( x \right) = \frac{1}{2}\frac{{\sqrt x }}{x}\].
D. \[f'\left( x \right) = x + \frac{{\sqrt x }}{2}\].
Tính đạo hàm của hàm số\(y = (x + 1)\sqrt {{x^2} + x + 1} \).
A. \(\frac{{4{x^2} - 5x + 3}}{{2\sqrt {{x^2} + x + 1} }}\)
B. \(\frac{{4{x^2} + 5x - 3}}{{2\sqrt {{x^2} + x + 1} }}\)
C. \(\frac{{4{x^2} + 5x + 3}}{{\sqrt {{x^2} + x + 1} }}\)
D. \(\frac{{4{x^2} + 5x + 3}}{{2\sqrt {{x^2} + x + 1} }}\)
Tính đạo hàm của hàm số\(y = {x^2} + x\sqrt {x + 1} \)
A. \(y' = 2x + \sqrt {x + 1} - \frac{x}{{2\sqrt {x + 1} }}\)
B. \(y' = 2x - \sqrt {x + 1} + \frac{x}{{2\sqrt {x + 1} }}\)
C. \(y' = \frac{x}{{2\sqrt {x + 1} }}\)
D. \(y' = 2x + \sqrt {x + 1} + \frac{x}{{2\sqrt {x + 1} }}\)
Tính đạo hàm của hàm số\(y = \frac{x}{{\sqrt {{a^2} - {x^2}} }}\)
A. \(y' = - \frac{{{a^2}}}{{\sqrt {{{({a^2} - {x^2})}^3}} }}\)
B. \(y' = \frac{{{a^2}}}{{\sqrt {{{({a^2} + {x^2})}^3}} }}\)
C. \(y' = \frac{{2{a^2}}}{{\sqrt {{{({a^2} - {x^2})}^3}} }}\)
D. \(y' = \frac{{{a^2}}}{{\sqrt {{{({a^2} - {x^2})}^3}} }}\)
Tính đạo hàm của hàm số\(y = \frac{1}{{x\sqrt x }}\)
A. \(y' = \frac{3}{2}\frac{1}{{{x^2}\sqrt x }}\)
B. \(y' = - \frac{1}{{{x^2}\sqrt x }}\)
C. \(y' = \frac{1}{{{x^2}\sqrt x }}\)
D. \(y' = - \frac{3}{2}\frac{1}{{{x^2}\sqrt x }}\)
Tính đạo hàm của hàm số\(y = \frac{{1 + x}}{{\sqrt {1 - x} }}\)
A. \(y' = \frac{{1 - 3x}}{{\sqrt {{{(1 - x)}^3}} }}\)
B. \(y' = \frac{{1 - 3x}}{{3\sqrt {{{(1 - x)}^3}} }}\)
C. \(y' = - \frac{1}{3}\frac{{1 - 3x}}{{2\sqrt {{{(1 - x)}^3}} }}\)
D. \(y' = \frac{{1 - 3x}}{{2\sqrt {{{(1 - x)}^3}} }}\)
Cho hàm số \(y = {\left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right)^2}\). Đạo hàm của hàm số \(f\left( x \right)\) là:
A. \(f'\left( x \right) = \frac{{ - 2\left( {1 - \sqrt x } \right)}}{{{{\left( {1 + \sqrt x } \right)}^3}}}\).
B. \(f'\left( x \right) = \frac{{ - 2\left( {1 - \sqrt x } \right)}}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^3}}}\).
C. \(f'\left( x \right) = \frac{{2\left( {1 - \sqrt x } \right)}}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}\).
D. \(f'\left( x \right) = \frac{{2\left( {1 - \sqrt x } \right)}}{{1 + \sqrt x }}\).
Hàm số \(f\left( x \right) = {\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^2}\)xác định trên \[D = \left( {0; + \infty } \right)\]. Có đạo hàm của \[f\left( x \right)\]là:
A. \[f'\left( x \right) = x + \frac{1}{x} - 2\].
B. \[f'\left( x \right) = x - \frac{1}{{{x^2}}}\].
C. \[f'\left( x \right) = \sqrt x - \frac{1}{{\sqrt x }}\].
D. \[f'\left( x \right) = 1 - \frac{1}{{{x^2}}}\].
Hàm số \(f\left( x \right) = {\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^3}\)xác định trên \[D = \left( {0; + \infty } \right)\]. Đạo hàm của hàm \[f\left( x \right)\]là:
A. \(f'\left( x \right) = \frac{3}{2}\left( {\sqrt x - \frac{1}{{\sqrt x }} - \frac{1}{{x\sqrt x }} + \frac{1}{{{x^2}\sqrt x }}} \right)\).
B. \(f'\left( x \right) = \frac{3}{2}\left( {\sqrt x + \frac{1}{{\sqrt x }} + \frac{1}{{x\sqrt x }} + \frac{1}{{{x^2}\sqrt x }}} \right)\).
C. \(f'\left( x \right) = \frac{3}{2}\left( { - \sqrt x + \frac{1}{{\sqrt x }} + \frac{1}{{x\sqrt x }} - \frac{1}{{{x^2}\sqrt x }}} \right)\).
D. \(f'\left( x \right) = x\sqrt x - 3\sqrt x + \frac{3}{{\sqrt x }} - \frac{1}{{x\sqrt x }}\).
Cho hàm số \(y = \frac{1}{{\sqrt {{x^2} + 1} }}\). Đạo hàm \(y'\) của hàm số là biểu thức nào sau đây?
A. \(\frac{x}{{({x^2} + 1)\sqrt {{x^2} + 1} }}\).
B. \( - \frac{x}{{({x^2} + 1)\sqrt {{x^2} + 1} }}\).
C. \(\frac{x}{{2({x^2} + 1)\sqrt {{x^2} + 1} }}\).
D. \( - \frac{{x({x^2} + 1)}}{{\sqrt {{x^2} + 1} }}\).
Cho hàm số \[f\left( x \right) = \sqrt {x - 1} + \frac{1}{{\sqrt {x - 1} }}\]. Để tính , hai học sinh lập luận theo hai cách:
(I) \[f\left( x \right) = \frac{x}{{\sqrt {x - 1} }} \Rightarrow f'\left( x \right) = \frac{{x - 2}}{{2\left( {x - 1} \right)\sqrt {x - 1} }}\].
(II) \[f\left( x \right) = \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\left( {x - 1} \right)\sqrt {x - 1} }} = \frac{{x - 2}}{{2\left( {x - 1} \right)\sqrt {x - 1} }}\].
Cách nào đúng?
A. Chỉ (I).
B. Chỉ (II)
C. Cả hai đều sai.
D. Cả hai đều đúng.
Cho hàm số \[y = f\left( x \right) = \left( {1 - 2{x^2}} \right)\sqrt {1 + 2{x^2}} \]. Ta xét hai mệnh đề sau:
(I) \[f'\left( x \right) = \frac{{ - 2x\left( {1 + 6{x^2}} \right)}}{{\sqrt {1 + 2{x^2}} }}\] (II) \[f\left( x \right).f'\left( x \right) = 2x\left( {12{x^4} - 4{x^2} - 1} \right)\]
Mệnh đề nào đúng?
A. Chỉ (II).
B. Chỉ (I).
C. Cả hai đều sai.
D. Cả hai đều đúng.
Đạo hàm của hàm số \(y = - 2{x^7} + \sqrt x \) bằng biểu thức nào sau đây?
A. \( - 14{x^6} + 2\sqrt x .\)
B. \( - 14{x^6} + \frac{2}{{\sqrt x }}.\)
C. \( - 14{x^6} + \frac{1}{{2\sqrt x }}.\)
D. \( - 14{x^6} + \frac{1}{{\sqrt x }}.\)
Đạo hàm của hàm số\[y = \sqrt {\frac{{2x - 1}}{{x + 2}}} \]là
A. \[y' = \frac{5}{{{{\left( {2x - 1} \right)}^2}}}.\sqrt {\frac{{x + 2}}{{2x - 1}}} .\]
B. \[y' = \frac{1}{2}.\frac{5}{{{{\left( {2x - 1} \right)}^2}}}.\sqrt {\frac{{x + 2}}{{2x - 1}}} .\]
C. \[y' = \frac{1}{2}.\sqrt {\frac{{x + 2}}{{2x - 1}}} .\]
D. \[y' = \frac{1}{2}.\frac{5}{{{{\left( {x + 2} \right)}^2}}}.\sqrt {\frac{{x + 2}}{{2x - 1}}} .\]
Đạo hàm của hàm số \(y = \frac{{\sqrt x }}{{1 - 2x}}\) bằng biểu thức nào sau đây?
A. \(\frac{1}{{2\sqrt x {{(1 - 2x)}^2}}}\).
B. \(\frac{1}{{ - 4\sqrt x }}\).
C. \(\frac{{1 - 2x}}{{2\sqrt x {{(1 - 2x)}^2}}}\).
D. \(\frac{{1 + 2x}}{{2\sqrt x {{(1 - 2x)}^2}}}\).
Đạo hàm của hàm số \[y = \frac{{2x - 3}}{{5 + x}} - \sqrt {2x} \]là:
A. \[y' = \frac{{13}}{{{{\left( {x + 5} \right)}^2}}} - \frac{1}{{\sqrt {2x} }}.\]
B. \[y' = \frac{{17}}{{{{\left( {x + 5} \right)}^2}}} - \frac{1}{{2\sqrt {2x} }}.\]
C. \[y' = \frac{{13}}{{{{\left( {x + 5} \right)}^2}}} - \frac{1}{{2\sqrt {2x} }}.\]
D. \[y' = \frac{{17}}{{{{\left( {x + 5} \right)}^2}}} - \frac{1}{{\sqrt {2x} }}.\]
Đạo hàm của hàm số\[y = \left( {2x - 1} \right)\sqrt {{x^2} + x} \]là:
A. \[y' = 2\sqrt {{x^2} + x} - \frac{{4{x^2} - 1}}{{2\sqrt {{x^2} + x} }}.\]
B. \[y' = 2\sqrt {{x^2} + x} + \frac{{4{x^2} - 1}}{{\sqrt {{x^2} + x} }}.\]
C. \[y' = 2\sqrt {{x^2} + x} + \frac{{4{x^2} - 1}}{{2\sqrt {{x^2} + x} }}.\]
D. \[y' = 2\sqrt {{x^2} + x} + \frac{{4{x^2} + 1}}{{2\sqrt {{x^2} + x} }}.\]
Đạo hàm của hàm số \(y = \frac{{x - 1}}{{\sqrt {{x^2} + 1} }}\) bằng biểu thức nào sau đây?
A. \(\frac{{2x}}{{\sqrt {{x^2} + 1} }}.\)
B. \(\frac{{1 + x}}{{\sqrt {{{({x^2} + 1)}^3}} }}.\)
C. \(\frac{{2(x + 1)}}{{\sqrt {{{({x^2} + 1)}^3}} }}.\)
D. \(\frac{{{x^2} - x + 1}}{{\sqrt {{{({x^2} + 1)}^3}} }}.\)
Đạo hàm của hàm số\[y = \frac{1}{{\sqrt {x + 1} - \sqrt {x - 1} }}\]là:
A. \[y' = - \frac{1}{{{{\left( {\sqrt {x + 1} + \sqrt {x - 1} } \right)}^2}}}.\]
B. \[y' = \frac{1}{{2\sqrt {x + 1} + 2\sqrt {x - 1} }}.\]
C. \[y' = \frac{1}{{4\sqrt {x + 1} }} + \frac{1}{{4\sqrt {x - 1} }}.\]
D. \[y' = \frac{1}{{2\sqrt {x + 1} }} + \frac{1}{{2\sqrt {x - 1} }}.\]
Cho hàm số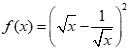 
. Hàm số có đạo hàm 
bằng:
A. 
.
B. 
.
C. 
.
D. 
.
Tính đạo hàm của hàm số\(y = \sqrt {{x^2} + 1} - \sqrt {1 - {x^2}} \)
A. \(\frac{1}{{\sqrt {{x^2} + 1} }} + \frac{x}{{\sqrt {1 - {x^2}} }}.\)
B. \(\frac{x}{{\sqrt {{x^2} + 1} }} + \frac{1}{{\sqrt {1 - {x^2}} }}.\)
C. \(\frac{1}{{\sqrt {{x^2} + 1} }} + \frac{1}{{\sqrt {1 - {x^2}} }}.\)
D. \(\frac{x}{{\sqrt {{x^2} + 1} }} + \frac{x}{{\sqrt {1 - {x^2}} }}.\)
\(y = \sqrt {\frac{{{x^2} + 1}}{x}} \).
A. \(\frac{1}{{\sqrt {\frac{{{x^2} + 1}}{x}} }}\left( {1 - \frac{1}{{{x^2}}}} \right)\)
B. \(\frac{1}{{2\sqrt {\frac{{{x^2} + 1}}{x}} }}\)
C. \(\frac{3}{{2\sqrt {\frac{{{x^2} + 1}}{x}} }}\left( {1 - \frac{1}{{{x^2}}}} \right)\)
D. \(\frac{1}{{2\sqrt {\frac{{{x^2} + 1}}{x}} }}\left( {1 - \frac{1}{{{x^2}}}} \right)\)
Tính đạo hàm của hàm số\(y = \left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right)\).
A. \(y' = 2\left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right).\frac{1}{{{{\left( {1 + \sqrt x } \right)}^2}}}\)
B. \(y' = 2\left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right).\frac{{ - 1}}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}\)
C. \(y' = \left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right).\frac{{ - 1}}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}\)
D. \(y' = 2\left( {\frac{{1 - \sqrt x }}{{1 + \sqrt x }}} \right).\frac{1}{{\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}\)
Tính đạo hàm của hàm số \(y = \sqrt {x - 1} + \frac{1}{{\sqrt {x - 1} }}\)
A. \(\frac{1}{{\sqrt {x - 1} }} + \frac{{ - 1}}{{2\sqrt {x - 1} \left( {x - 1} \right)}}.\)
B. \(\frac{1}{{2\sqrt {x - 1} }} + \frac{{ - 1}}{{2\sqrt {x - 1} }}.\)
C. \(\frac{1}{{\sqrt {x - 1} }} + \frac{{ - 1}}{{\sqrt {x - 1} \left( {x - 1} \right)}}.\)
D. \(\frac{1}{{2\sqrt {x - 1} }} + \frac{{ - 1}}{{2\sqrt {x - 1} \left( {x - 1} \right)}}.\)
Tính đạo hàm của hàm số \(y = {\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^5}\).
A. \(5{\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^4}\left( {\frac{1}{{2\sqrt x }} + \frac{1}{{2\sqrt x .x}}} \right)\)
B. \(5{\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^4}\left( {\frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x .x}}} \right)\)
C. \({\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^4}\left( {\frac{1}{{2\sqrt x }} + \frac{1}{{2\sqrt x .x}}} \right)\)
D. \(5{\left( {\sqrt x - \frac{1}{{\sqrt x }}} \right)^4}\left( {\frac{1}{{2\sqrt x }} + \frac{1}{{2\sqrt x .x}}} \right)\)
Tính đạo hàm của hàm số\(y = \frac{{1 + x}}{{\sqrt {1 - x} }}\).
A. \(\frac{{ - x}}{{2\sqrt {1 - x} \left( {1 - x} \right)}}.\)
B. \(\frac{{3 - x}}{{\sqrt {1 - x} \left( {1 - x} \right)}}.\)
C. \(\frac{3}{{2\sqrt {1 - x} \left( {1 - x} \right)}}.\)
D. \(\frac{{3 - x}}{{2\sqrt {1 - x} \left( {1 - x} \right)}}.\)
Tính đạo hàm của hàm số\(y = \sqrt {x + \sqrt {x + \sqrt x } .} \)
A. \(\frac{1}{{2\sqrt {x + \sqrt {x + \sqrt x } } }}.\left[ {1 + \frac{1}{{2\sqrt {x + \sqrt x } }}.\left( {1 + \frac{1}{{2\sqrt x }}} \right)} \right].\)
B. \(\frac{1}{{\sqrt {x + \sqrt {x + \sqrt x } } }}.\left[ {1 + \frac{1}{{\sqrt {x + \sqrt x } }}.\left( {1 + \frac{1}{{\sqrt x }}} \right)} \right].\)
C. \(\frac{1}{{\sqrt {x + \sqrt {x + \sqrt x } } }}.\left[ {1 + \frac{1}{{2\sqrt {x + \sqrt x } }}.\left( {1 + \frac{1}{{2\sqrt x }}} \right)} \right].\)
D. \(\frac{1}{{2\sqrt {x + \sqrt {x + \sqrt x } } }}.\left[ {1 - \frac{1}{{2\sqrt {x + \sqrt x } }}.\left( {1 + \frac{1}{{2\sqrt x }}} \right)} \right].\)
Tính đạo hàm của hàm số\(y = \frac{{4x + 1}}{{\sqrt {{x^2} + 2} }}\) (áp dụng u chia v đạo hàm)
A. \(\frac{{ - x}}{{\left( {{x^2} + 2} \right)\sqrt {{x^2} + 2} }}\)
B. \(\frac{{x + 8}}{{\left( {{x^2} + 2} \right)\sqrt {{x^2} + 2} }}\)
C. \(\frac{{ - x + 8}}{{\left( {{x^2} + 3} \right)\sqrt {{x^2} + 2} }}\)
D. \(\frac{{ - x + 8}}{{\left( {{x^2} + 2} \right)\sqrt {{x^2} + 2} }}\)
Tính đạo hàm của hàm số \(y = \sqrt {\frac{{{x^3}}}{{x - 1}}} \) (Áp dụng căn bặc hai của u đạo hàm).
A. \(y' = \frac{1}{{2\sqrt {\frac{{{x^3}}}{{x - 1}}} }}.\frac{{{x^3} - 3{x^2}}}{{{{\left( {x - 1} \right)}^2}}}.\)
B. \(y' = \frac{1}{{2\sqrt {\frac{{{x^3}}}{{x - 1}}} }}.\frac{{2{x^3} - {x^2}}}{{{{\left( {x - 1} \right)}^2}}}.\)
C. \(y' = \frac{1}{{\sqrt {\frac{{{x^3}}}{{x - 1}}} }}.\frac{{2{x^3} - 3{x^2}}}{{{{\left( {x - 1} \right)}^2}}}.\)
D. \(y' = \frac{1}{{2\sqrt {\frac{{{x^3}}}{{x - 1}}} }}.\frac{{2{x^3} - 3{x^2}}}{{{{\left( {x - 1} \right)}^2}}}.\)
Tính đạo hàm của hàm số\(y = \sqrt {{{\left( {x - 2} \right)}^3}} .\)
A. \(\frac{{\left( {x - 2} \right)}}{{2\sqrt {x - 2} }}.\)
B. \(\frac{{\left( {x - 2} \right)}}{{\sqrt {x - 2} }}.\)
C. \(\frac{{3\left( {x - 2} \right)}}{{\sqrt {x - 2} }}.\)
D. \(\frac{{3\left( {x - 2} \right)}}{{2\sqrt {x - 2} }}.\)
Tính đạo hàm của hàm số \(y = {\left( {1 + \sqrt {1 - 2x} } \right)^3}\).
A. \(\frac{{ - 6{{\left( {1 + \sqrt {1 - 2x} } \right)}^2}}}{{\sqrt {1 - 2x} }}.\)
B. \(\frac{{ - {{\left( {1 + \sqrt {1 - 2x} } \right)}^2}}}{{2\sqrt {1 - 2x} }}.\)
C. \(\frac{{ - {{\left( {1 + \sqrt {1 - 2x} } \right)}^2}}}{{\sqrt {1 - 2x} }}.\)
D. \(\frac{{ - 6{{\left( {1 + \sqrt {1 - 2x} } \right)}^2}}}{{2\sqrt {1 - 2x} }}.\)
Tính đạo hàm của hàm số\(y = \sqrt {\sqrt {{x^2} + 1} + 2x - 1} \)
A. \(y' = \frac{{x + 2\sqrt {{x^2} + 1} }}{{\sqrt {({x^2} + 1)\left( {\sqrt {{x^2} + 1} + 2x - 1} \right)} }}\)
B. \(y' = \frac{{x + \sqrt {{x^2} + 1} }}{{\sqrt {({x^2} + 1)\left( {\sqrt {{x^2} + 1} + 2x - 1} \right)} }}\)
C. \(y' = \frac{{x + \sqrt {{x^2} + 1} }}{{2\sqrt {({x^2} + 1)\left( {\sqrt {{x^2} + 1} + 2x - 1} \right)} }}\)
D. \(y' = \frac{{x + 2\sqrt {{x^2} + 1} }}{{2\sqrt {({x^2} + 1)\left( {\sqrt {{x^2} + 1} + 2x - 1} \right)} }}\)
Cho hàm số \[y = f(x) = \left\{ \begin{array}{l}{x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x \ge 1\\2x - 1\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,\,x < 1\end{array} \right.\]. Hãy chọn câu sai:
A. \[f'\left( 1 \right) = 1\].
B. Hàm số có đạo hàm tại \[{x_0} = 1\].
C. Hàm số liên tục tại \[{x_0} = 1\].
D. \[f'(x) = \left\{ \begin{array}{l}2x\,\,\,\,\,\,{\rm{khi}}\,\,\,x \ge 1\\2\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,\,x < 1\end{array} \right..\]
Tính đạo hàm của hàm số\(f(x) = \left\{ \begin{array}{l}{x^2} + x + 1{\rm{ khi }}x \le 1\\\sqrt {x - 1} + 3{\rm{ khi }}x > 1\end{array} \right.\)
A. \(f'(x) = \left\{ \begin{array}{l}2x{\rm{ khi }}x < 1\\\frac{1}{{2\sqrt {x - 1} }}{\rm{ khi }}x > 1\end{array} \right.\)
B. \(f'(x) = \left\{ \begin{array}{l}2x + 1{\rm{ khi }}x < 1\\ - \frac{1}{{\sqrt {x - 1} }}{\rm{ khi }}x > 1\end{array} \right.\)
C. \(f'(x) = \left\{ \begin{array}{l}2x + 1{\rm{ khi }}x < 1\\\frac{1}{{\sqrt {x - 1} }}{\rm{ khi }}x > 1\end{array} \right.\)
D. \(f'(x) = \left\{ \begin{array}{l}2x + 1{\rm{ khi }}x < 1\\\frac{1}{{2\sqrt {x - 1} }}{\rm{ khi }}x > 1\end{array} \right.\)
Tìm \(a,b\) để các hàm số sau có đạo hàm trên \(\mathbb{R}\). \(f(x) = \left\{ \begin{array}{l}{x^2} - x + 1{\rm{ }}\,\,\,\,{\rm{khi }}x \le 1\\ - {x^2} + ax + b{\rm{ khi }}x > 1\end{array} \right.\)
A. \(\left\{ \begin{array}{l}a = 13\\b = - 1\end{array} \right.\)
B. \(\left\{ \begin{array}{l}a = 3\\b = - 11\end{array} \right.\)
C. \(\left\{ \begin{array}{l}a = 23\\b = - 21\end{array} \right.\)
D. \(\left\{ \begin{array}{l}a = 3\\b = - 1\end{array} \right.\)
Tính đạo hàm của hàm số\(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} + x + 1}}{{x + 1}}{\rm{ khi }}x \ge 0\\{x^2} + ax + b{\rm{ khi }}x < 0\end{array} \right.\).
A. \(a = 0,b = 11\)
B. \(a = 10,b = 11\)
C. \(a = 20,b = 21\)
D. \(a = 0,b = 1\)
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
