164 CÂU HỎI
Giá trị nhỏ nhất của hàm số trên khoảng (0; 2) là
A. 1
B. 3
C. 0
D. -1
Cho hàm số .
Khẳng định nào sau đây đúng?
A.
B.
C.
D. Hàm số không tồn tại giá trị lớn nhất
Gọi a là giá trị lớn nhất của hàm số trên khoảng
Khi đó giá trị của biểu thức bằng
A.
B.
C.
D.
Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A.
B.
C.
D. Hàm số không có giá trị nhỏ nhất
Giá trị nhỏ nhất của hàm số trên (2; 6) là
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên khoảng là
A.
B.
C.
D.
Mệnh đề nào sau đây là đúng với hàm số trên tập xác định của nó?
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất
C. Hàm số có giá trị lớn nhất và có giá trị nhỏ nhất
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất
Giá trị nhỏ nhất của hàm số trên khoảng là
A. Không tồn tại
B. -3
C..
D. 0
Cho hàm số . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên [0; 3]. Giá trị của bằng
A. 8
B. 10
C. 6
D. 4
Giá trị lớn nhất của hàm số trên [-1; 2] là
A. 29
B. 1
C. 3
D.
Cho hàm số . Giá trị của bằng
A. 16
B.
C.
D.
Giá trị lớn nhất của hàm số trên đoạn [1; 3] bằng
A.
B.
C. -3
D. -4
Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
Giá trị của biểu thức bằng
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên đoạn [0; 5] bằng 5 khi m bằng
A. 6
B. 10
C. 7
D. 5
Gọi A, B là giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn [2; 3]. Tất cả các giá trị thực của tham số m để là
A.
B.
C.
D.
Biết hàm số (với m là tham số) trên đoạn [-2; 0] đạt giá trị lớn nhất bằng 6. Các giá trị của tham số m là
A.
B.
C.
D.
Giá trị lớn nhất, giá trị nhỏ của hàm số trên đoạn [-1; 1] lần lượt là a, b thì giá trị của bằng
A. 4
B. 3
C. 0
D. 1
Giá trị nhỏ nhất của hàm số trên đoạn [-1; 4] bằng
A. 48
B. 52
C. -102
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn [1; 2] bằng 2.
Số phần tử của tập S là
A. 3
B. 1
C. 4
D. 2
Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng
A. 108
B. 120
C. 210
D. 136
Biết giá trị lớn nhất của hàm số bằng 18.
Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Biết rằng giá trị lớn nhất của hàm số trên đoạn [-2; 1] đạt giá trị nhỏ nhất, giá trị của tham số m bằng
A. 1
B. 3
C. 4
D. 5
Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì m bằng
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số đạt giá trị lớn nhất bằng
A. 2
B. 5
C. 8
D. 9
Giá trị nhỏ nhất của hàm số đạt giá trị lớn nhất bằng
A. 7
B. -7
C. 0
D. 4
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Khi đó có giá trị bằng
A. -6
B. -12
C. 12
D. 3
Trên đoạn hàm số đạt giá trị lớn nhất tại
A.
B.
C.
D.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên . Tổng có giá trị là
A. -12
B. -6
C. 18
D. -4
Giá trị nhỏ nhất của hàm số trên tập xác định là
A.
B. -1
C. 1
D.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn là
A.
B.
C.
D.
Với giá trị nào của tham số m thì hàm số đạt giá trị lớn nhất trên đoạn bằng 2?
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số trên đoạn bằng 0 khi
A.
B.
C.
D.
Với những giá trị nào của tham số m thì hàm số đạt giá trị lớn nhất trên đoạn bằng ?
A.
B.
C.
D.
Giá trị lớn nhất của hàm số trên đoạn [-5; 5] bằng 2018. Trong các khẳng định dưới đây khẳng định nào đúng?
A.
B.
C.
D.
Để giá trị lớn nhất của hàm số trên đoạn là nhỏ nhất thì giá trị của m thuộc khoảng nào dưới đây?
A.
B.
C.
D.
Gọi M là giá trị lớn nhất của hàm số trên đoạn , là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số trên đoạn [0,2] đạt giá trị nhỏ nhất. Khi đó giá trị của tham số m bằng
A. 26
B. 13
C. 14
D. 27
Biết rằng giá trị lớn nhất của hàm số trên đoạn [0; 2] đạt giá trị nhỏ nhất. Khi đó giá trị của tham số m bằng
A. -12
B. -13
C. -14
D. -11
Xét hàm số với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên đoạn . Khi M nhận giá trị nhỏ nhất thì bằng
A. 5
B. -4
C. 2
D. -3
Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn bằng 16. Số phần tử của S là
A. 0
B. 2
C. 4
D. 1
Gọi S là tập hợp các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn [0; 2] bằng 3. Số phần tử của S là
A. 0
B. 2
C. 3
D. 1
Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn bằng 50. Tổng các phần tử của tập S là
A. 4
B. 36
C. 140
D. 0
Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn không vượt quá 20. Tổng các phần tử của S bằng
A. 210
B. -195
C. 105
D. 300
Cho hàm số . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn . Có bao nhiêu số nguyên a thuộc đoạn sao cho ?
A. 7
B. 5
C. 6
D. 4
Giá trị nhỏ nhất của hàm số đạt giá trị lớn nhất khi tham số m bằng
A. 2020
B. 2019
C. 0
D. 2018
Giá trị nhỏ nhất của hàm số đạt giá trị lớn nhất bằng
A.6
B. -6
C. 0
D. 10
Cho hàm số liên tục trên R và có bảng biến thiên như hình vẽ
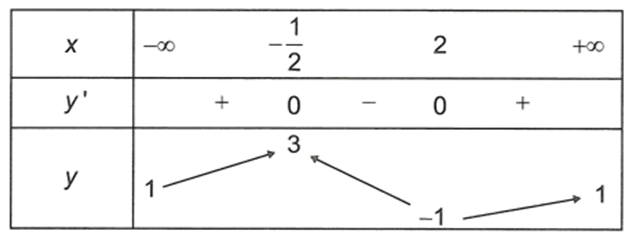
Giá trị lớn nhất của hàm số trên R là
A.
B.
C.
D.
Hàm số liên tục trên R và có bảng biến thiên như hình bên dưới
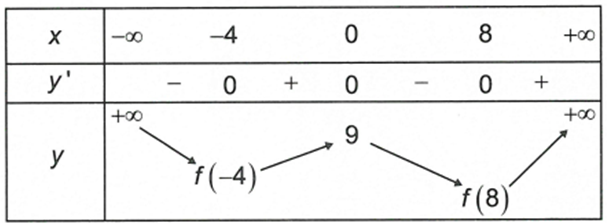
Biết , khi đó giá trị nhỏ nhất của hàm số đã cho trên R bằng
A. 9
B.
C.
D. -4
Cho hàm số xác định trên tập hợp và có bảng biến thiên như sau
![Cho hàm số y= f(x) xác định trên tập hợp D=( âm vô cùng, -1] hợp [1,3/2] và có bảng biến thiên như sau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid0-1673791029.png)
Khẳng định đúng là
A. ; không tồn tại
B. ;
C. ;
D. ; không tồn tại
Cho hàm số có đồ thị trên khoảng như hình bên dưới
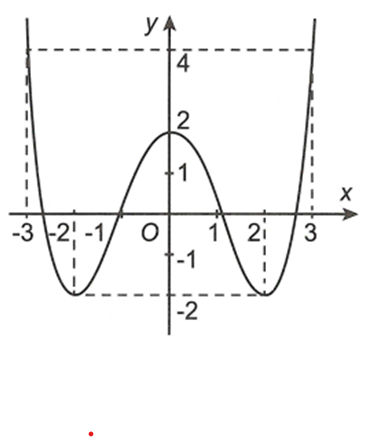 Khẳng định đúng là
Khẳng định đúng là
A. Giá trị lớn nhất của hàm số bằng 3
B. Giá trị lớn nhất của hàm số bằng 4
C. Giá trị nhỏ nhất của hàm số bằng -3
D. Hàm số không có giá trị lớn nhất
Cho hàm số liên tục và có bảng biến thiên trên đoạn như sau
![Cho hàm số y= f(x) liên tục và có bảng biến thiên trên đoạn [0,2] như sau Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid3-1673792513.png)
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn là
A. và m=1
B. M=0 và m=2
C. M=2 và m=0
C. M=1 và m=4
Cho hàm số liên tục và có bảng biến thiên trên đoạn như sau
![Cho hàm số y=f(x) liên tục và có bảng biến thiên trên đoạn [-2,4] như sau Giá trị lớn nhất của hàm số y=f(x) trên đoạn [-2,4] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid4-1673793318.png)
Giá trị lớn nhất của hàm số trên đoạn bằng
A.
B.
C.
D.
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ bên dưới.
![Cho hàm số y=f(x) liên tục trên đoạn [-1,3] và có đồ thị như hình vẽ bên dưới. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid5-1673793734.png)
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của bằng
A. 1
B. 3
C. 4
D. 5
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ.
![Cho hàm số y=f(x) liên tục trên đoạn [-1,1] và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid6-1673793972.png)
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của bằng
A. 0
B. 1
C. 2
D. 3
Cho đồ thị hàm số như hình vẽ
![Cho đồ thị hàm số y=f'(x) như hình vẽ Hàm số y=f(x) đạt giá trị lớn nhất trên khoảng [1,3] tại x0 . (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid7-1673794125.png)
Hàm số đạt giá trị lớn nhất trên khoảng tại . Khi đó giá trị của bằng bao nhiêu?
A. 2018
B. 2019
C. 2021
D. 2022
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số là
A.
B.
C.
D.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng
A.
B.
C.
D. 3
Giá trị lớn nhất M của hàm số là
A.
B.
C.
D.
Cho hàm số (với m là tham số thực).
Giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất khi m bằng
A.
B.
C.
D.
Giá trị nhỏ nhất của biểu thức bằng
A.
B.
C. 1
D.
Giá trị lớn nhất của hàm số trên đoạn là
A.
B.
C.
D.
Cho hàm số có bảng biến thiên như sau
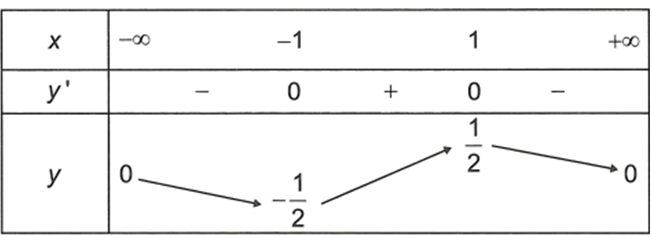
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là M, m. Giá trị biểu thức là
A.
B.
C. 2
D. 1
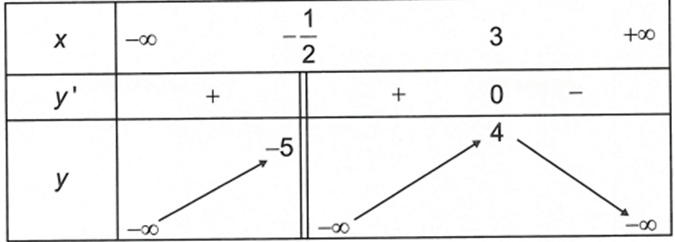
Cho hàm số xác định và liên tục trên khoảng ,
và có bảng biến thiên như sau
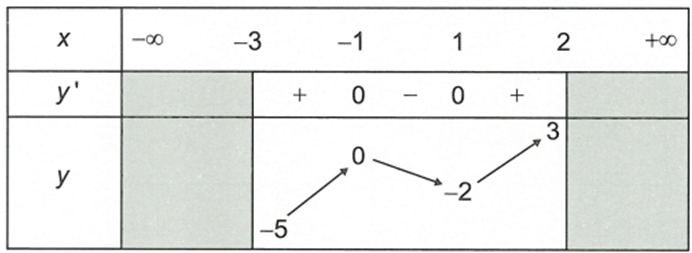
Mệnh đề nào dưới đây đúng?
A. Hàm số không có giá trị nhỏ nhất trên khoảng
B. Giá trị nhỏ nhất của hàm số bằng -5
C. Giá trị lớn nhất của hàm số bằng 3
D. Giá trị lớn nhất của hàm số trên khoảng bằng 0.
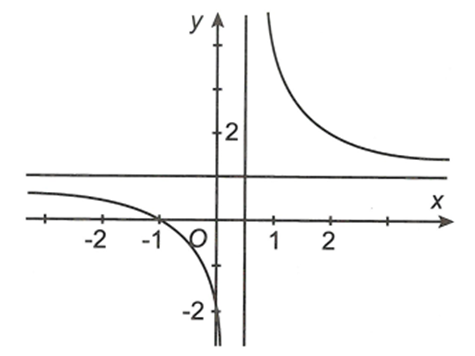
Cho hàm số có đồ thị trên khoảng như hình bên. Khẳng định đúng là
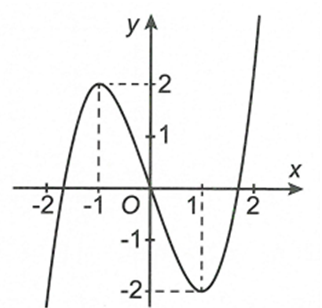
A. Giá trị lớn nhất của hàm số bằng 2
B. Giá trị lớn nhất của hàm số bằng 1
C. Giá trị nhỏ nhất của hàm số bằng -1
D. Hàm số không có giá trị lớn nhất
Cho hàm số liên tục trên và có bảng biến thiên như sau
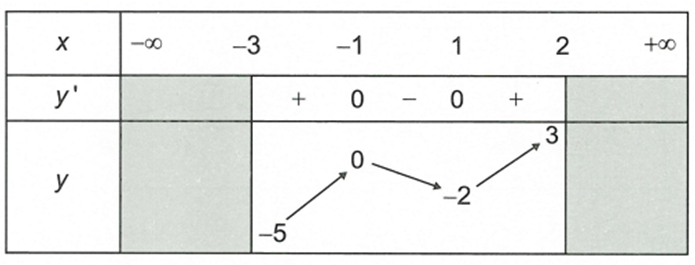
Mệnh đề nào sau đây đúng?
A. Hàm số không có giá trị nhỏ nhất và không có giá trị lớn nhất trên [-5; 3)
B. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất trên [-5; 3)
C. Hàm số có giá trị nhỏ nhất và có giá trị lớn nhất trên [-5; 3)
D. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất trên [-5; 3)
Cho hàm số liên tục trên và có bảng biến thiên như sau
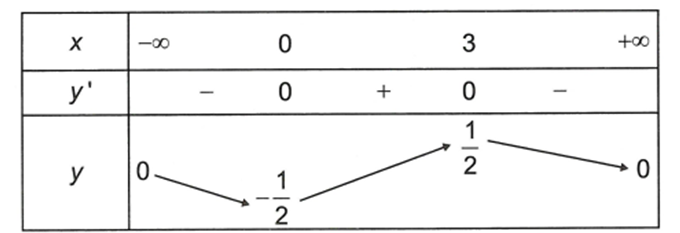
Mệnh đề nào sau đây đúng?
A. Hàm số không có giá trị nhỏ nhất và không có giá trị lớn nhất
B. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất
C. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất
D. Hàm số có giá trị nhỏ nhất và có giá trị lớn nhất
Cho hàm số liên tục và có bảng biến thiên trong đoạn như sau
![Cho hàm số y=f(x) liên tục và có bảng biến thiên trong đoạn [-6,0] như sau Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid15-1673798446.png)
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn là
A. M=7 và m=0
B. M=0 và m=6
C. M=6 và m=7
D. M=0 và m=7
Cho hàm số liên tục trên đoạn và có bảng biến thiên như sau
![Cho hàm số y=f(x) liên tục trên đoạn [-1, 4] và có bảng biến thiên như sau Mệnh đề nào sau đây sai (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid16-1673798646.png)
Mệnh đề nào sau đây sai
A. Hàm số không có giá trị lớn nhất trên khoảng
B. Hàm số không có giá trị lớn nhất trên nửa khoảng
C. Hàm số không có giá trị nhỏ nhất trên nửa khoảng
D. Hàm số không có giá trị nhỏ nhất trên đoạn
Cho hàm số liên tục trên và có bảng biến thiên như sau
Mệnh đề nào sau đây đúng?
A. Hàm số không có giá trị nhỏ nhất và không có giá trị lớn nhất
B. Hàm số không có giá trị nhỏ nhất và có giá trị lớn nhất
C. Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất
D. Hàm số có giá trị nhỏ nhất và có giá trị lớn nhất
Cho hàm số liên tục trên và có bảng biến thiên như sau
![Cho hàm số y=f(x) liên tục trên [-1,3] và có bảng biến thiên như sau Giá trị nhỏ nhất của hàm số y=f(x)+2 bằng trên đoạn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid18-1673799022.png)
Giá trị nhỏ nhất của hàm số bằng trên đoạn bằng
A.-4
B. -1
C. -3
D. -2
Cho hàm số liên tục trên đoạn R và có đồ thị như hình vẽ
![Cho hàm số y=f(x) liên tục trên đoạn R và có đồ thị như hình vẽ Giá trị nhỏ nhất trên đoạn [ -1,1] của hàm số là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid19-1673799174.png)
Giá trị nhỏ nhất trên đoạn của hàm số là
A.
B.
C.
D.
Cho đồ thị hàm số như hình vẽ
![Cho đồ thị hàm số y=f'(x) như hình vẽ Hàm số y=f(x) đạt giá trị nhỏ nhất trên đoạn [0; 2] tại x bằng bao nhiêu? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid20-1673799350.png)
Hàm số đạt giá trị nhỏ nhất trên đoạn [0; 2] tại x bằng bao nhiêu?
A.
B.
C. x=1
D. x=2
Cho hàm số xác định và liên tục trên khoảng và . Đồ thị hàm số là đường cong trong hình vẽ dưới đây
Tìm mệnh đề đúng trong các mệnh đề sau
A.
B.
C.
D.
Giá trị lớn nhất của hàm số bằng
A.
B. -5
C.
D. 3
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số lần lượt là
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số bằng
A.
B. -2
C. -4
D. 2
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số là
A.
B.
C. M= 5, m= -2
D.
Giá trị nhỏ nhất m của hàm số là
A.
B.
C.
D.
Giá trị lớn nhất của hàm số trên đoạn là
A.
B.
C.
D.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số theo thứ tự là
A.
B.
C.
D.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số theo thứ tự là
A.
B.
C.
D.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số theo thứ tự là
A. 4 và
B. 4 và
C. 2 và
D. và
Giá trị lớn nhất của hàm số là
A.
B.
C.
D.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng
A. 1
B. 2
C. 3
D. 5
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Khi đó tỉ số bằng
A.
B.
C. 9
D.
Cho biểu thức với . Giá trị nhỏ nhất của P bằng
A. 3
B.
C. 1
D. 4
Cho hai số thực x,y thỏa mãn và . Giá trị nhỏ nhất và giá trị lớn nhất của biểu thức lần lượt là
A. và 1
B. 0 và 1
C. và 1
D. 1 và 2
Cho x, y là các số thực thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
A. 3
B.
C.
D.
Gọi là ba số thực dương sao cho biểu thức
đạt giá trị nhỏ nhất.
Tổng bằng
A. 3
B. 1
C.
D.
Cho x,y là các số thực dương thỏa mãn điều kiện .
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức bằng
A. 8
B. 0
C. 12
D. 4
Cho x, y, z là ba số thực thuộc đoạn và . Giá trị nhỏ nhất của biểu thức
bằng
A.
B.
C.
D. 1
Cho các số thực x, y thay đổi nhưng luôn thỏa mãn . Giá trị nhỏ nhất của biểu thức thuộc khoảng nào sau đây?
A. ( 4,7)
B. (-2,1)
C. (1,4)
D. (7,10)
Cho x, y là hai số thực không âm thỏa mãn . Giá trị lớn nhất của biểu thức
là
A.
B.
C.
D.
Cho hai số thực x, y thỏa mãn . Giá trị nhỏ nhất của là
A.
B.
C.
D.
Cho hai số thực x, y thỏa mãn và biểu thức . Gọi M, m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của P. Tổng là
A.
B.
C.
D.
Cho x, y là các số thực thỏa mãn và biểu thức . Gọi M, m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của P. Tổng bằng
A.
B.
C.
D.
Cho các số thực x, y dương thỏa mãn và . Gọi M, m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của . Tổng là
A.
B.
C.
D.
Cho các số thực dương x, y, z. Giá trị nhỏ nhất của biểu thức bằng
A.
B.
C.
D.
Cho a, b, c không âm phân biệt. Giá trị nhỏ nhất của biểu thức
bằng
A.
B.
C. 11
D. 13
Xét ba số thực a; b; c thay đổi thuộc đoạn . Giá trị lớn nhất của biểu thức
bằng
A.
B. 0
C.
D.
Cho x, y, z là các số thực thỏa mãn . Giá trị lớn nhất của biểu thức bằng
A.
B.
C.
D.
Cho a, b, c là các số thực không âm thỏa mãn . Giá trị lớn nhất của biểu thức bằng
A.
B.
C.
D.
Cho và . Giá trị nhỏ nhất của biểu thức là
A.
B.
C.
D.
Cho và . Giá trị nhỏ nhất của biểu thức bằng
A.
B.
C.
D.
Cho hàm số y = f(x) liên tục trên tập R và có bảng biến thiên như sau
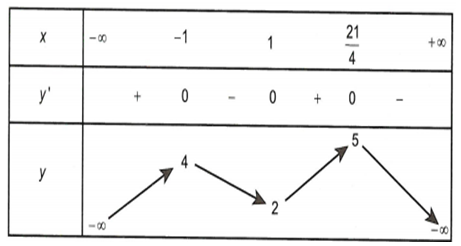
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tìm khẳng định đúng trong các khẳng định sau.
A.
B.
C.
D.
Cho hàm số có bảng biến thiên như sau
![Cho hàm số y= f(x) có bảng biến thiên như sau Hàm số y= (|x-1|) có giá trị nhỏ nhất trên đoạn [0,2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid2-1673858523.png)
Hàm số có giá trị nhỏ nhất trên đoạn bằng
A.
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ. Khi đó hàm số đạt giá trị nhỏ nhất trên bằng
![Cho hàm số y=f(x) có đồ thị như hình vẽ. Khi đó hàm số y=f(2-x^2) đạt giá trị nhỏ nhất trên [0,căn 2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid0-1674048148.png)
A.
B.
C.
D.
Cho hàm số xác định và liên tục trên R và có bảng biến thiên sau
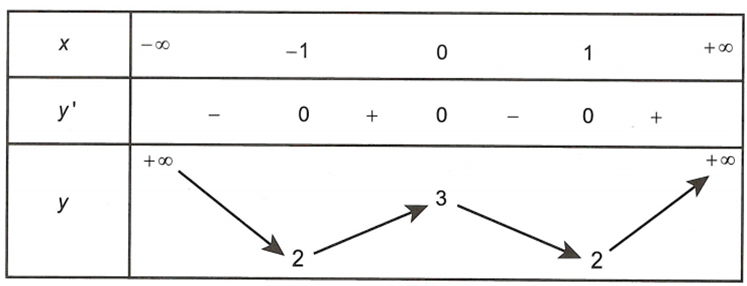
Giá trị nhỏ nhất của hàm số trên đoạn là
A. 64
B. 65
C. 66
D. 67
Cho hàm số có đạo hàm và liên tục trên R. Biết rằng đồ thị hàm số như dưới đây.
Lập hàm số .
Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Cho hàm số liên tục trên R và có bảng biến thiên như sau
![Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau Gọi M là giá trị lớn nhất của hàm số y=g(x)=f(3-x) trên [0,3] . (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid3-1674050041.png)
Gọi M là giá trị lớn nhất của hàm số trên . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Cho hàm số có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Khi đó bằng
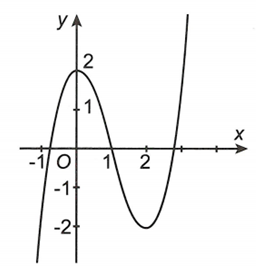
A. 3
B. 1
C. 2
D. 0
Cho hàm số liên tục trên R và có bảng biến thiên như sau
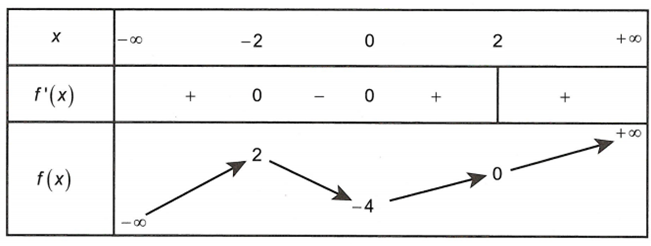
Hàm số đạt giá trị lớn nhất và nhỏ nhất lần lượt là M và m. Mệnh đề nào dưới đây đúng
A.
B.
C.
D.
Cho hàm số liên tục trên và có bảng biến thiên như sau
![Cho hàm số y=f(x) liên tục trên [-2,4] và có bảng biến thiên như sau Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid6-1674050581.png)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số . Giá trị của bằng
A. 4
B. -4
C. 2
D. 1
Cho hàm số liên tục trên R và có đồ thị như hình vẽ dưới đây. Khi đó giá trị lớn nhất của hàm số trên nửa khoảng là
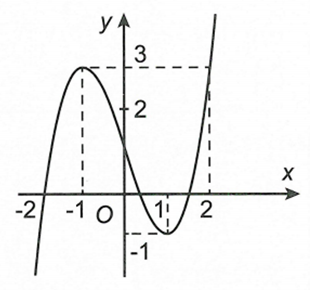
A. 3
B. -1
C. 0
D. không tồn tại
Cho hàm số liên tục trên R và có đồ thị như hình vẽ dưới đây.
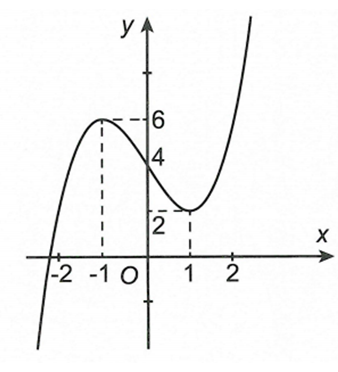
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên . Tổng bằng
A. 4
B. 6
C. 8
D. 12
Cho hàm số liên tục trên R và có đồ thị như hình vẽ bên. Gọi M, m theo thứ tự là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tổng bằng
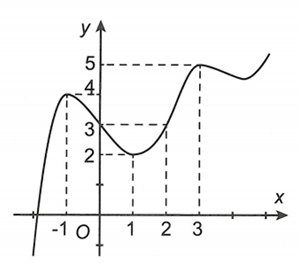
A. 9
B. 8
C. 7
D. 1
Cho hàm số có bảng biến thiên như hình vẽ
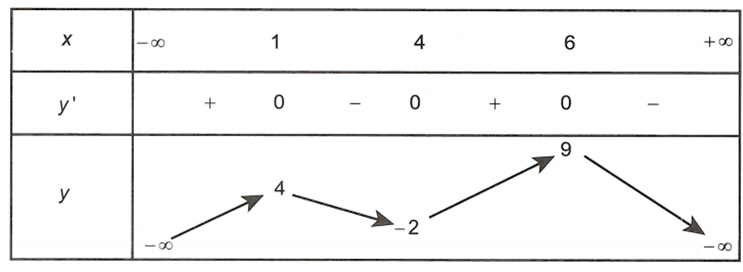
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn lần lượt là M, m. Tổng bằng
A. 13
B. 7
C.
D. 2
Cho hàm số liên tục trên và có đồ thị như hình vẽ
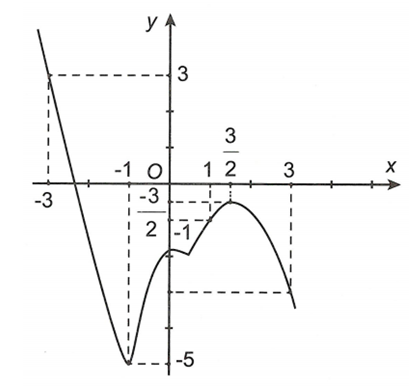
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tổng bằng
A.
B.
C.
D.
Cho hàm số , biết hàm số có đồ thị như hình vẽ dưới đây. Hàm số đạt giá trị nhỏ nhất trên đoạn tại điểm nào sau đây?
![Cho hàm số y=f(x) , biết hàm số y=f'(x) có đồ thị như hình vẽ dưới đây. Hàm số y=f(x) đạt giá trị nhỏ nhất trên đoạn [1/2,3/2] tại điểm nào (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid12-1674051738.png)
A.
B.
C. x=1
D. x=0
Cho hàm số có đạo hàm . Hàm số liên tục trên R và có đồ thị như hình vẽ. Biết . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên bằng
A.
B. 198
C.
D.
Cho hàm số liên tục trên R. Đồ thị của hàm số như hình vẽ. Đặt . Mệnh đề nào dưới đây đúng?
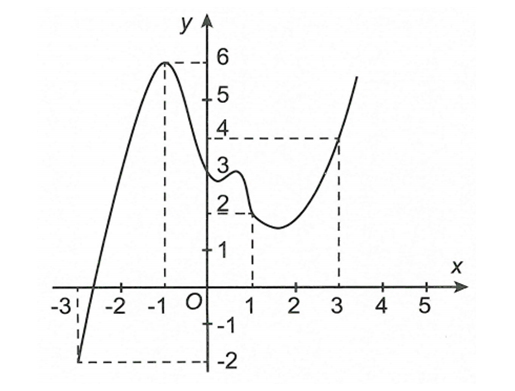
A.
B.
C.
D. Không tồn tại giá trị nhỏ nhất của trên .
Cho hàm số có đồ thị như hình vẽ.
Xét hàm số . Mệnh đề nào dưới đây đúng?
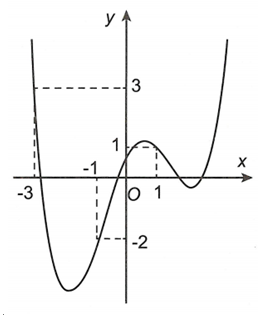
A.
B.
C.
D.
Cho hàm số ,hàm số có đồ thị như hình vẽ
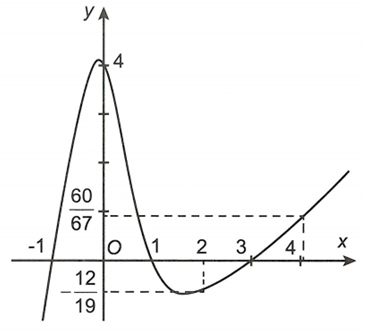
Giá trị nhỏ nhất của hàm số trên khoảng bằng
A.
B.
C.
D.
Cho hàm số . Biết hàm số có đồ thị như hình vẽ. Trên đoạn ,hàm số đạt giá trị nhỏ nhất tại điểm
![Cho hàm số y=f(x) . Biết hàm số y=f'(x) có đồ thị như hình vẽ. Trên đoạn [-4,3] ,hàm số g(x)=2f(x)+(1-x)^2 đạt giá trị nhỏ nhất tại điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid1-1674052710.png)
A.
B.
C.
D.
Một chất điểm chuyển động theo quy luật . Thời điểm t (giây) mà tại đó vận tốc của chất điểm chuyển động đạt giá trị lớn nhất là
A. t = 2s
B. t = 5s
C. t = 1s
D. t =3s
Một vật chuyển động theo quy luật với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 180 (m/s)
B. 36 (m/s)
C. 144 (m/s)
D. 24 (m/s)
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ
B. 1 giờ
C. 3 giờ
D. 2 giờ
Người ta xây một bể chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể là đồng / . Hãy xác định kích thước của bể sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là
A. 75 triệu đồng
B. 85 triệu đồng
C. 90 triệu đồng
D. 95 triệu đồng
Bác Hoàng có một tấm thép mỏng hình tròn, tâm O, bán kính 4 dm. Bác định cắt ra một hình quạt tròn tâm O, quấn rồi hàn ghép hai mép của hình quạt tròn lại để tạo thành một đồ vật dạng mặt nón tròn xoay (tham khảo hình vẽ). Dung tích lớn nhất có thể của đồ vật mà bác Hoàng tạo ra bằng bao nhiêu? (bỏ qua phần mối hàn và độ dày của tấm thép)
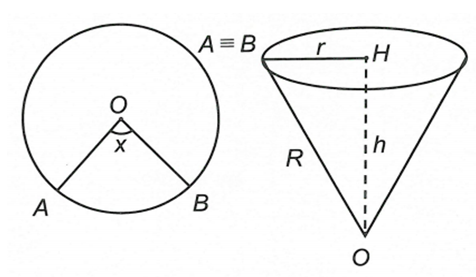
A.
B.
C.
D.
Người ta làm chiếc thùng phi dạng hình trụ, kín hai đáy, với thể tích theo yêu cầu là . Hỏi bán kính đáy R và chiều cao h của thùng phi bằng bao nhiêu để khi làm thì tiết kiệm vật liệu nhất
A.
B.
C.
D.
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như hình vẽ. Khoảng cách từ C đến B là 1 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 4km. Tổng chi phí lắp đặt cho 1km dây điện trên biển là 40 triệu đồng, còn trên đất liền là 20 triệu đồng. Tính tổng chi phí nhỏ nhất để hoàn thành công việc trên (làm tròn đến hai chữ số sau dấu phẩy)
A. 120 triệu đồng
B. 164,92 triệu đồng
C. 114,64 triệu đồng
D. 106,25 triệu đồng
Một chất điểm chuyển động theo quy luật . Thời điểm t (giây) mà tại đó vận tốc của chất điểm chuyển động đạt giá trị lớn nhất là
A. t = 2s
B. t = 5s
C. t = 1s
D. t =3s
Một vật chuyển động theo quy luật với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 180 (m/s)
B. 36 (m/s)
C. 144 (m/s)
D. 24 (m/s)
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ
B. 1 giờ
C. 3 giờ
D. 2 giờ
Một vật chuyển động theo quy luật với t (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216 (m/s)
B. 30 (m/s)
C. 400 (m/s)
D. 54 (m/s)
Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s (mét) đi được của đoàn tàu là một hàm số của thời gian t (giây), hàm số đó là . Thời điểm t (giây) mà tại đó vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất là
A. t = 2s
B. t = 6s
C. t = 8s
D. t = 4s
Một chất điểm chuyển động có phương trình chuyển động là , với t (s) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (m) là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 6 giây đầu tiên, vận tốc v (m/s) của chất điểm đạt giá trị lớn nhất bằng
A. 29 m/s
B. 26 m/s
C. 17 m/s
D. 36 m/s
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức , trong đó x là liều lượng thuốc được tiêm cho bệnh nhân ( x được tính bằng miligam). Liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất là
A. x = 8
B. x = 10
C. x = 15
D. x = 7
Để thiết kế một chiếc bể cá không có nắp đậy hình hộp chữ nhật có chiều cao 60cm, thể tích là , người thợ dùng loại kính để sử dụng làm mặt bên có giá thành là 70.000 đồng / và loại kính để làm mặt đáy có giá thành là 100.000 đồng /. Chi phí thấp nhất để làm bể cá là
A. 28.300 đồng
B. 38.200 đồng
C. 83.200 đồng
D. 83.200 đồng
Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và bốn mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi h là chiều cao của hộp để giá thành làm chiếc hộp là thấp nhất. biết với m, n là các số nguyên dương nguyên tố cùng nhau. Tổng m + n bằng
A. 12
B. 13
C. 11
D. 10
Một người thợ xây, muốn xây một bồn chứa thóc hình trụ tròn với thể tích là (như hình vẽ). Đáy làm bằng bê tông, thành làm bằng tôn và nắp bể làm bằng nhôm. Biết giá thành các vật liệu như sau: bê tông 100 nghìn đồng một , tôn 90 nghìn một và nhôm 120 nghìn đồng một . Chi phí thấp nhất để làm bồn chứa thóc (làm tròn đến hàng nghìn) là
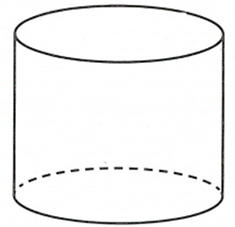
A. 15038000 đồng
B. 15037000 đồng
C. 15039000 đồng
D. 15040000 đồng
Một công ty dự kiến chi 1 tỉ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100.000 đồng / , chi phí để làm mặt đáy là 120.000 đồng /. Số thùng sơn tối đa mà công ty đó sản xuất được (giả sử chi phí cho các mối nối không đáng kể) là
A. 58135 thùng
B. 18209 thùng
C. 12525 thùng
D. 57582 thùng
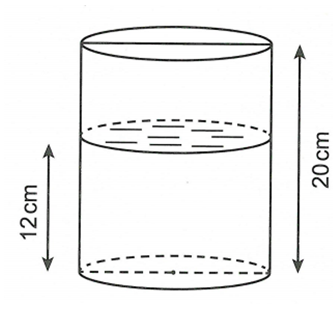
Một cốc hình trụ có bán kính đáy là 2cm, chiều cao 20cm. Trong cốc đang có một ít nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (hình vẽ). Một con quạ muốn uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm. Con quạ thông minh mổ những viên đá hình cầu có bán kính 0,6cm thả vào cốc để mực nước dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên đá?
A. 30
B. 27
C. 28
D. 29
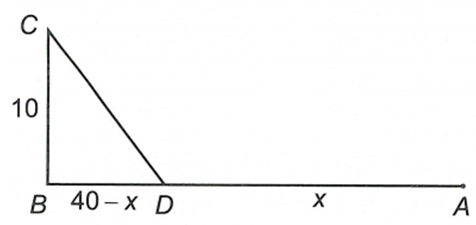
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là 5 USD/km, đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất?
A.
B.
C.
D.
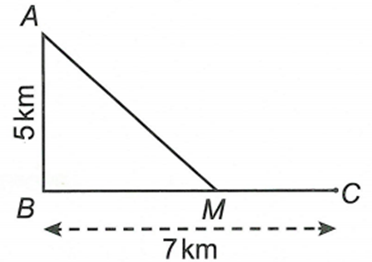
Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng AB = 5 (km). Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7(km). Người canh hải đăng có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ từ M đến C với vận tốc 6 (km/h). Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau đây để người đó đến kho nhanh nhất?
A.
B.
C.
D.
Thầy Toản có thanh gỗ dài là 3,2 m. Thầy Toản dự định dùng thanh gỗ để thiết kế 5 hình tam giác giống nhau làm kệ trang trí phòng đọc sách, trong đó các tam giác có 1 cạnh có độ dài là 24 cm (coi các mẩu cắt bỏ đi không đáng kể). Tổng diện tích của 5 tam giác có giá trị lớn nhất là

A.
B.
C.
D.
Một kĩ sư được một công ty xăng dầu thuê thiết kế một mẫu bồn chứa xăng với thể tích V cho trước, hình dạng như hình vẽ bên, các kích thước r, h thay đổi sao cho nguyên vật liệu làm bồn xăng là ít nhất. Người kĩ sư này phải thiết kế kích thước h như thế nào để đảm bảo được đúng yêu cầu mà công ty xăng dầu đã đưa ra?
A.
B.
C.
D.
Một kĩ sư được một công ty xăng dầu thuê thiết kế một mẫu bồn chứa xăng với thể tích V cho trước, hình dạng như hình vẽ bên, các kích thước r, h thay đổi sao cho nguyên vật liệu làm bồn xăng là ít nhất. Người kĩ sư này phải thiết kế kích thước h như thế nào để đảm bảo được đúng yêu cầu mà công ty xăng dầu đã đưa ra?
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m trong đoạn để phương trình có nghiệm thực?
A. 100
B.101
C. 102
D. 103
Cho phương trình ( m là tham số). Biết rằng tập hợp các giá trị của tham số m để phương trình có nghiệm thuộc đoạn là đoạn . Giá trị của biểu thức là
A.
B.
C.
D.
Giá trị nhỏ nhất của tham số m để hệ phương trình có nghiệm là Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Các giá trị của tham số m để bất phương trình có nghiệm trên khoảng là
A.
B.
C.
D.
Gọi S là tập hợp các giá trị nguyên của tham số để bất phương trình nghiệm đúng với mọi . Số các phần tử của tập S là
A. 1
B. 2020
C. 2019
D. 2
Cho hàm số liên tục trên và có đồ thị như hình vẽ. Bất phương trình có nghiệm thuộc khi và chỉ khi
![Cho hàm số y=f(x) liên tục trên [-1,3] và có đồ thị như hình vẽ. Bất phương trình f(x)+căn x+1 + căn 7-x >=m có nghiệm thuộc [-1,3] khi và chỉ khi (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid9-1674312068.png)
A.
B.
C.
D.
Gọi S là tập tất cả các giá trị nguyên âm của tham số m để phương trình có nghiệm. Tập S có số phần tử là
A. 10
B. 6
C. 4
D. 2
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm thực phân biệt ?
A. 3
B. 4
C. 5
D. 6
Cho phương trình (m là tham số). Gọi p, q lần lượt là các giá trị m nguyên nhỏ nhất và giá trị lớn nhất thuộc để phương trình có nghiệm. Khi đó giá trị là
A. 10
B. 19
C. 20
D. 8
Biết rằng tập hợp tất cả giá trị của tham số m để phương trình có nghiệm thực là . Tổng là
A.
B.
C.
D.
Có tất cả bao nhiêu số tự nhiên m để bất phương trình có nghiệm?
A. 2
B. 3
C. 4
D. 5
Tất cả các giá trị của tham số m để bất phương trình nghiệm đúng với mọi là
A.
B.
C.
D.
Có bao nhiêu số nguyên để bất phương trình nghiệm đúng với mọi
A. 2017
B. 2018
C. 2019
D. 2020
Tổng các giá trị nguyên của để bất phương trình có nghiệm là
A. -195
B. -175
C. -165
D. -162
Có bao nhiêu giá trị của tham số để hệ phương trình có nghiệm
A. 4
B. 5
C. 2014
D. 2015
Cho hệ phương trình . Có bao nhiêu giá trị nguyên của tham số để hệ phương trình có nghiệm?
A. 2018
B. 2019
C. 2017
D. 2016

