30 CÂU HỎI
Hệ phương trình  nhận cặp số nào sau đây là nghiệm?
nhận cặp số nào sau đây là nghiệm?
A. 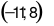 .
.
B. 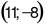 .
.
C.  .
.
D. 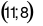 .
.
Hệ phương trình \[\left\{ \begin{array}{l}x + y = 3\\x + 2y = - 5\end{array} \right.\] nhận cặp số nào sau đây là nghiệm?
A. \(\left( { - 11;\,\,8} \right)\).
B. \(\left( {11;\,\, - 8} \right)\).
C. \(\left( { - 11;\,\, - 8} \right)\).
D. \(\left( {11;\,\,8} \right)\).
Cho hệ phương trình 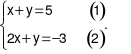 Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, cách đơn giản nhất là
Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, cách đơn giản nhất là
A. Cộng từng vế của phương trình (1) với phương trình (2).
B. Trừ từng vế của phương trình (1) cho phương trình (2).
C. Nhân hai vế phương trình (1) với 2 rồi trừ từng vế của phương trình mới cho phương trình (2).
D. Nhân hai vế phương trình (1) với 2 rồi cộng từng vế của phương trình mới với phương trình (2).
Cho hệ phương trình \[\left\{ \begin{array}{l}x + y = 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\2x + y = - 3\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, cách đơn giản nhất là
A. Cộng từng vế của phương trình (1) với phương trình (2).
B. Trừ từng vế của phương trình (1) cho phương trình (2).
C. Nhân hai vế phương trình (1) với 2 rồi trừ từng vế của phương trình mới cho phương trình (2).
D. Nhân hai vế phương trình (1) với 2 rồi cộng từng vế của phương trình mới với phương trình (2).
Cho hệ phương trình \[\left\{ \begin{array}{l} - 2x + 2y = - 1\\3x + y = 7\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp thế (biểu diễn \(y\) theo \(x)\), ta được hệ thức biểu diễn \(y\) theo \(x\) là
A. \[y = 7 + 3x.\]
B. \[y = 7 - 3x.\]
C. \[y = 3x - 7.\]
D. \[y = - 1 + 2x.\]
Cho hệ phương trình  Khi giải hệ phương trình bằng phương pháp thế (biểu diễn
Khi giải hệ phương trình bằng phương pháp thế (biểu diễn 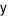 theo
theo  , ta được hệ thức biểu diễn
, ta được hệ thức biểu diễn 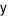 theo
theo 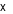 là
là
A. 
B. 
C. 
D. 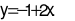
Cho hệ phương trình \[\left\{ \begin{array}{l}4x + 7y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\ - x - 5y = 0\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right..\] Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, một trong những cách đơn giản nhất là
A. Cộng từng vế của phương trình (1) với phương trình (2).
B. Trừ từng vế của phương trình (1) cho phương trình (2).
C. Nhân hai vế phương trình (1) với 5 và nhân hai vế phương trình (2) với 7, rồi cộng từng vế của hai phương trình mới với nhau.
D. Nhân phương trình (2) với 4 rồi cộng từng vế của phương trình mới với phương trình (1).
Cho hệ phương trình 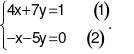 Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, một trong những cách đơn giản nhất là
Khi giải hệ phương trình bằng phương pháp cộng đại số, để được phương trình bậc nhất một ẩn, một trong những cách đơn giản nhất là
A. Cộng từng vế của phương trình (1) với phương trình (2).
B. Trừ từng vế của phương trình (1) cho phương trình (2).
C. Nhân hai vế phương trình (1) với 5 và nhân hai vế phương trình (2) với 7, rồi cộng từng vế của hai phương trình mới với nhau.
D. Nhân phương trình (2) với 4 rồi cộng từng vế của phương trình mới với phương trình (1).
Để mở chương trình giải hệ phương trình bậc nhất hai ẩn bằng máy tính cầm tay, ta ấn liên tiếp các phím:
A. 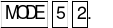
B. 
C. 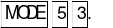
D. 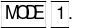
Để mở chương trình giải hệ phương trình bậc nhất hai ẩn bằng máy tính cầm tay, ta ấn liên tiếp các phím:
A.
B.
C.
D.
Biết hệ phương trình nhận cặp số
nhận cặp số 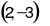 là một nghiệm. Khi đó, giá trị của
là một nghiệm. Khi đó, giá trị của 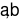 là
là
A. 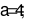
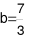 .
.
B. 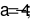
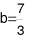 .
.
C. 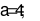
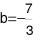 .
.
D. 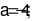
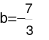 .
.
II. Thông hiểu
Biết hệ phương trình \[\left\{ \begin{array}{l}ax - 3y = 1\\x + by = - 5\end{array} \right.\] nhận cặp số \(\left( {2;\,\, - 3} \right)\) là một nghiệm. Khi đó, giá trị của \(a,\,\,b\) là
A. \[a = 4;\] \[b = \frac{7}{3}\].
B. \[a = - 4;\] \[b = \frac{7}{3}\].
C. \[a = 4;\] \[b = - \frac{7}{3}\].
D. \[a = - 4;\] \[b = - \frac{7}{3}\].
Hệ phương trình  nhận cặp số nào sau đây là nghiệm?
nhận cặp số nào sau đây là nghiệm?
A.  .
.
B.  .
.
C.  .
.
D.  .
.
Hệ phương trình \[\left\{ \begin{array}{l}3\left( {x + y} \right) + 2\left( {x - y} \right) = 6\\\left( {x + y} \right) + 3\left( {x - y} \right) = 4\end{array} \right.\] nhận cặp số nào sau đây là nghiệm?
A. \(\left( {\frac{8}{7};\,\,\frac{2}{7}} \right)\).
B. \(\left( { - \frac{8}{7};\,\,\frac{2}{7}} \right)\).
C. \(\left( {\frac{8}{7};\,\, - \frac{2}{7}} \right)\).
D. \(\left( { - \frac{8}{7};\,\, - \frac{2}{7}} \right)\).
Cho hệ phương trình 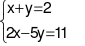 có nghiệm là
có nghiệm là  . Khi đó tổng của
. Khi đó tổng của 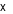 và
và 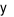 bằng
bằng
A.  .
.
B. 3.
C. 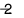
D. 2.
Cho hệ phương trình \[\left\{ \begin{array}{l}x + y = 2\\2x - 5y = 11\end{array} \right.\] có nghiệm là \(\left( {x;\,\,y} \right)\). Khi đó tổng của \(x\) và \(y\) bằng
A. \[ - 1\].
B. 3.
C. \[ - 2.\]
D. 2.
Cho hệ phương trình 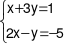 có nghiệm là
có nghiệm là  . Tổng lập phương của
. Tổng lập phương của 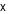 và
và 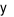 là
là
A.  .
.
B.  .
.
C. 1.
D. 5.
Cho hệ phương trình \[\left\{ \begin{array}{l}x + 3y = 1\\2x - y = - 5\end{array} \right.\] có nghiệm là \(\left( {x;\,\,y} \right)\). Tổng lập phương của \(x\) và \(y\) là
A. \( - 1\).
B. \( - 7\).
C. 1.
D. 5.
Cho hệ phương trình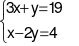 có nghiệm là
có nghiệm là  . Bình phương hiệu hai số
. Bình phương hiệu hai số 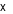 và
và 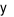 bằng
bằng
A. 25.
B. 35.
C. 37.
D. 49.
Cho hệ phương trình \[\left\{ \begin{array}{l}3x + y = 19\\x - 2y = 4\end{array} \right.\] có nghiệm là \(\left( {x;\,\,y} \right)\). Bình phương hiệu hai số \(x\) và \(y\) bằng
A. 25.
B. 35.
C. 37.
D. 49.
Cho hệ phương trình có nghiệm là
có nghiệm là  . Tổng bình phương của
. Tổng bình phương của 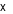 và
và 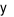 là
là
A. 1.
B. 85.
C. 169.
D. 181.
Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {y + 1} \right) = xy - 2\\\left( {x + 2} \right)\left( {y - 1} \right) = xy + 6\end{array} \right.\] có nghiệm là \(\left( {x;\,\,y} \right)\). Tổng bình phương của \(x\) và \(y\) là
A. 1.
B. 85.
C. 169.
D. 181.
Với giá trị nào của 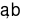 để đồ thị hàm số
để đồ thị hàm số 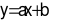 đi qua hai điểm
đi qua hai điểm  và
và 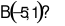
A. 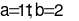 .
.
B. 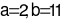 .
.
C. 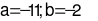 .
.
D. 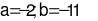 .
.
Với giá trị nào của \[a,{\rm{ }}b\] để đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {1;\,\,13} \right)\) và \(B\left( { - 5;\,\,1} \right)?\)
A. \(a = 11;\,\,b = 2\).
B. \(a = 2;\,\,b = 11\).
C. \(a = - 11;\,\,b = - 2\).
D. \(a = - 2;\,\,b = - 11\).
Cho  là nghiệm của hệ phương trình
là nghiệm của hệ phương trình và cùng với các khẳng định sau:
và cùng với các khẳng định sau:
(i) Hệ phương trình cho điều kiện xác định là 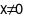 và
và 
(ii) Hệ phương trình có nghiệm là 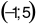 .
.
(iii) Tổng bình phương của 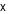 và
và 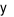 lớn hơn 20.
lớn hơn 20.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 0.
B. 1.
C. 2.
D. 3.
III. Vận dụng
Cho \(\left( {x;\,\,y} \right)\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}\frac{3}{x} + \frac{2}{y} = 7\\\frac{2}{x} - \frac{5}{y} = - 27\end{array} \right.\] và cùng với các khẳng định sau:
(i) Hệ phương trình cho điều kiện xác định là \(x \ne 0\) và \(y \ne 0.\)
(ii) Hệ phương trình có nghiệm là \(\left( { - 1;\,\,5} \right)\).
(iii) Tổng bình phương của \(x\) và \(y\) lớn hơn 20.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 0.
B. 1.
C. 2.
D. 3.
Với giá trị nào của tham số  thì hệ phương trình
thì hệ phương trình có nghiệm duy nhất
có nghiệm duy nhất 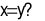
A. 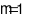 .
.
B. 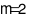 .
.
C. 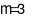 .
.
D. 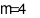 .
.
Với giá trị nào của tham số \[m\] thì hệ phương trình \[\left\{ \begin{array}{l}2x + y = 3\\\left( {2m + 1} \right)x + 2y = 7\end{array} \right.\] có nghiệm duy nhất \(x = y?\)
A. \(m = 1\).
B. \(m = 2\).
C. \(m = 3\).
D. \(m = 4\).
Có bao nhiêu giá trị nguyên của  để hệ phương trình
để hệ phương trình 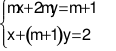 có nghiệm duy nhất
có nghiệm duy nhất 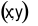 sao cho
sao cho  nhận giá trị nguyên?
nhận giá trị nguyên?
A. 1.
B. 2.
C. 3.
D. 4.
Có bao nhiêu giá trị nguyên của \[m\] để hệ phương trình \[\left\{ \begin{array}{l}mx + 2my = m + 1\\x + \left( {m + 1} \right)y = 2\end{array} \right.\] có nghiệm duy nhất \[\left( {x;y} \right)\] sao cho \[G = x - y\] nhận giá trị nguyên?
A. 1.
B. 2.
C. 3.
D. 4.

