15 CÂU HỎI
I. Nhận biết
Cho các hình dưới đây:
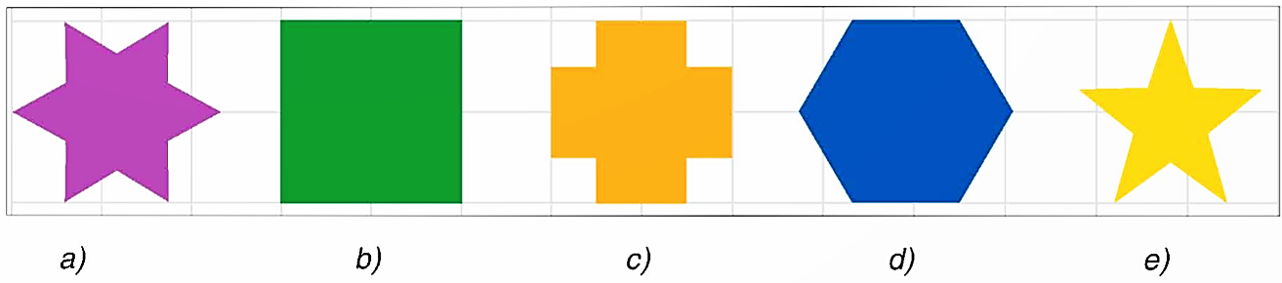
Trong các hình trên, hình nào có dạng là đa giác đều?
A. Hình \(a,\,\,b\).
B. Hình \(b,\,\,d\).
C. Hình \[c,\,\,e\].
D. Hình \(d,\,\,e\).
Đa giác đều là một đa giác
A. Có 3 cạnh và 3 góc bằng nhau.
B. Có 7 cạnh và 7 góc bằng nhau.
C. Có các cạnh và các góc bằng nhau.
D. Có 8 cạnh và 8 góc bằng nhau.
Các phép quay có thể có với một đa giác đều tâm \[O\] là
A. Phép quay thuận chiều và phép quay đảo chiều.
B. Phép quay thuận chiều và phép quay ngược chiều.
C. Phép quay xuôi chiều và phép quay đảo chiều.
D. Phép quay xuôi chiều và phép quay ngược chiều.
Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.
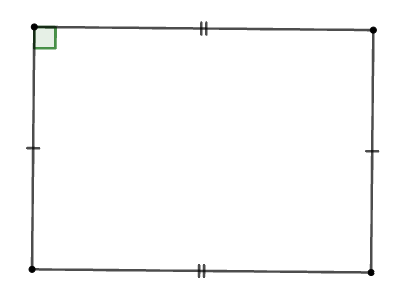
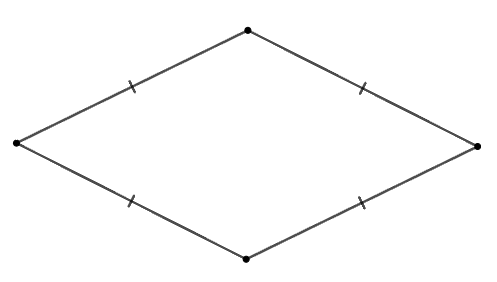
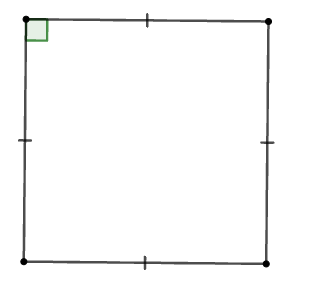
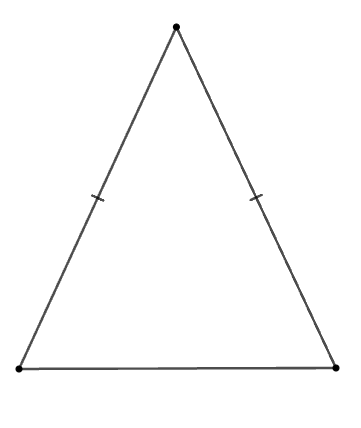
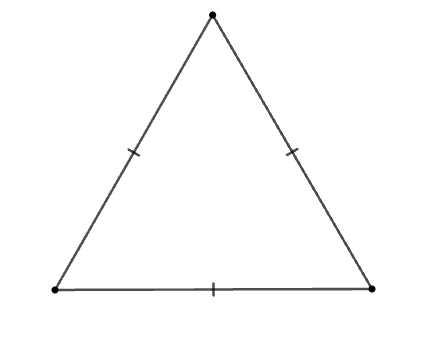
Trong các hình trên, có bao nhiêu đa giác giác đều?
A. 1.
B. 2.
C. 3.
D. 4.
Với một phép quay góc \(\alpha \) thì \(\alpha \) có thể nhận các giá trị:
A. \(0^\circ \le \alpha \le 180^\circ \).
B. \(0^\circ < \alpha < 180^\circ \).
</>
C. \(0^\circ \le \alpha \le 360^\circ \).
D. \(0^\circ < \alpha < 360^\circ \).
II. Thông hiểu
Mỗi góc của bát giác đều nội tiếp đường tròn tâm \[O\] có số đo là
A. \(120^\circ \).
B. \(150^\circ \).
C. \(90^\circ \).
D. \(135^\circ \).
Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là \(5{\rm{ cm}}\). Chu vi đa giác đều này là
A. 45 cm.
B. 50 cm.
C. 60 cm.
D. 55 cm.
Cho ngũ giác đều\[ABCDE\]. Khẳng định nào sau đây là sai?
A. Ngũ giác đều\[ABCDE\] có một tâm đối xứng.
B. Mỗi góc trong của ngũ giác đều \[ABCDE\] là \(108^\circ \).
C. Tổng các góc trong của ngũ giác đều \[ABCDE\] là \(450^\circ \).
D. Tổng các góc trong của ngũ giác đều \[ABCDE\] là \(540^\circ \).
Cho hình vuông tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến hình vuông trên thành chính nó là
A. 1.
B. 2.
C. 3.
D. 4.
Cho tam giác đều tâm \[O\]. Số phép quay thuận chiều tâm \[O\] góc α với \[0^\circ \le \alpha < 360^\circ \], biến tam giác trên thành chính nó là
</>
A. 1.
B. 2.
C. 3.
D. 4.
Cho hình thoi \[ABCD\] có góc \(\widehat {ABC} = 60^\circ \). Phép quay thuận chiều tâm \[A\] một góc \(60^\circ \) biến cạnh \[CD\] thành
A. \[AB\].
B. \[BC\].
C. \[CD\].
D. \[DA\].
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Phép quay thuận chiều tâm \[O\] biến điểm \[A\] thành điểm \[E\] thì điểm \[C\] biến thành điểm
A. \[A\].
B. \[B\].
C. \[D\].
D. \[E\].
III. Vận dụng
Cho lục giác đều \[ABCDEF\] tâm \[O.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[EF,{\rm{ }}BD.\] Khẳng định nào sau đây là sai?
A. \[N\] là trung điểm \[OC.\]
B. \[\Delta AFM = \Delta AON.\]
C. Tam giác \[AMN\] đều.
D. Cả A, B, C đều sai.
Một lục giác đều và một ngũ giác đều chung cạnh \[AD\] (như hình vẽ).
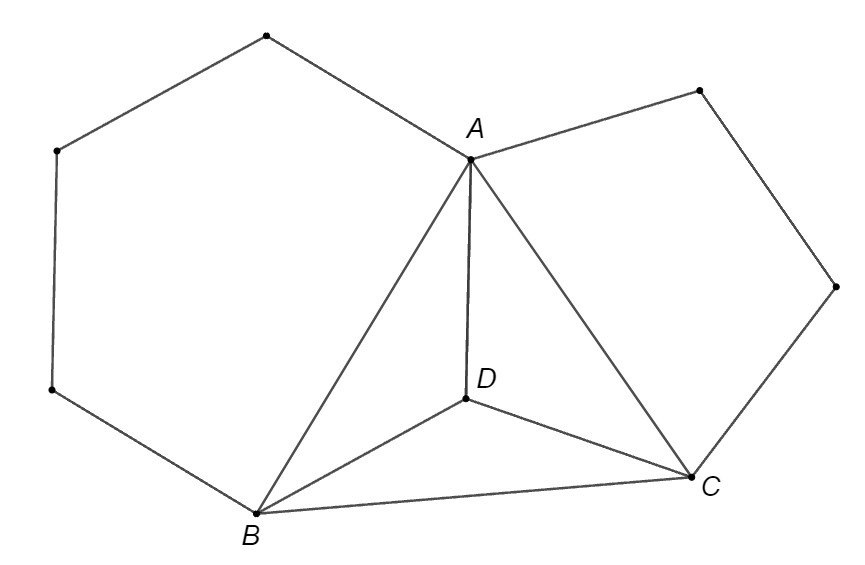
Số đo góc \(BAC\) là
A. \(30^\circ \).
B. \(36^\circ \).
C. \(60^\circ \).
D. \(66^\circ \).
Cho bát giác đều \[ABCDEFGH\] có tâm \[O.\] Phép quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm nào?
A. \[G.\]
B. \[A.\]
C. \[E.\]
D. \[H.\]
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải