15 câu hỏi
Kết luận nào sau đây là sai khi nói về đồ thị hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)?\)
Đồ thị hàm số nhận trục tung làm trục đối xứng.
Với \(a < 0\) thì đồ thị nằm phía dưới trục hoành và \(O\left( {0;0} \right)\) là điểm cao nhất của đồ thị.
Với \(a > 0\) thì đồ thị nằm phía trên trục hoành và \(O\left( {0;0} \right)\) là điểm cao nhất của đồ thị.
Với \(a > 0\) thì đồ thị nằm phía trên trục hoành và \(O\left( {0;0} \right)\) là điểm thấp nhất của đồ thị.
Điểm đối xứng với điểm \(\left( {x;y} \right)\) qua trục \(Oy\)là
\(\left( {0;0} \right).\)
\(\left( { - x;y} \right).\)
\(\left( {x;y} \right).\)
\[\left( {x; - y} \right).\]
Cho đồ thị của một hàm số bậc hai sau:
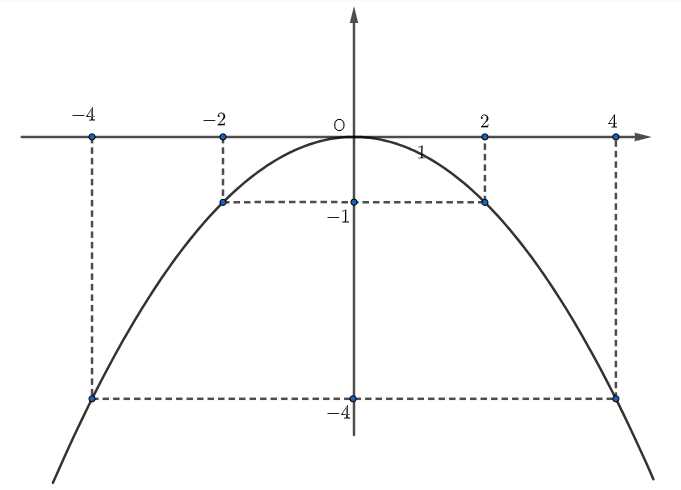
Hệ số \(a\) của đồ thị hàm số bậc hai này là
\(a = - 1.\)
\[a = 1.\]
\(a < 0.\)
\(a > 0.\)
II. Thông hiểu
Điểm nào sau đây thuộc đồ thị hàm số \(y = 3{x^2}\,?\)
\(\left( { - 1\,;\, - 3} \right).\)
\[\left( {4\,;\,\,12} \right).\]
\(\left( { - 2\,;\,\, - 6} \right).\)
\(\left( {1\,;\,\,3} \right).\)
Trong mặt phẳng tọa độ \[Oxy\], cho hàm số \(y = \left( {m + 2} \right){x^2}\) có đồ thị đi qua điểm \(\left( { - 1\,;\,\,3} \right).\) Khi đó giá trị của \[m\] tương ứng là
\(m = - 1.\)
\(m = 1.\)
\(m = 0.\)
\(m = 2.\)
Để vẽ được đồ thị hàm số \(y = \frac{{ - 1}}{4}{x^2}\) cần xác định các điểm nào sau đây?
\(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
\(\left( { - 4;\,\,4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
\(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\,1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
\(\left( { - 4;\,\, - 4} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\,1} \right);\,\,\left( {4;\,\, - 4} \right).\)
Cho hàm số \(y = - 2{x^2}\) có đồ thị là \(\left( P \right).\) Tọa độ các điểm thuộc \(\left( P \right)\) có tung độ bằng \( - 6\) là
\(\left( {\sqrt 3 ;\, - 6} \right);\,\,\left( { - \sqrt 3 ;\, - 6} \right).\)
\(\left( { - 6;\,\sqrt 3 } \right);\,\,\left( { - 6;\, - \sqrt 3 } \right).\)
\(\left( {\sqrt 3 ;\, - 6} \right).\)
\(\left( { - 72; - 6} \right).\)
I. Nhận biết
Hàm số \(y = \left( {m + 2} \right){x^2}\) đạt giá trị nhỏ nhất khi
\(m < - 2.\)
\(m \le - 2.\)
\(m > - 2.\)
\(m \ge - 2.\)
Trong mặt phẳng tọa độ \(Oxy,\) biết điểm có hoành độ bằng 1 là một điểm chung của parabol \(y = 2{x^2}\) và đường thẳng \(y = \left( {m - 1} \right)x - 2,\) với \(m\) là tham số. Khi đó giá trị của \(m.\)
\(m = 1.\)
\(m = 5.\)
\(m = 2.\)
\(m = 3.\)
Đồ thị của hình bên dưới là đồ thị của hàm số nào trong các hàm số sau?
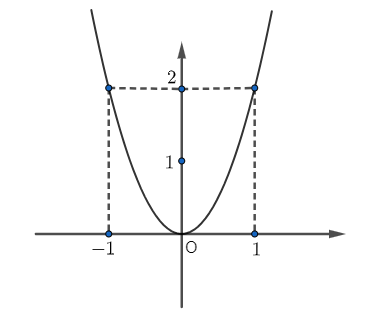
\(y = 4{x^2}.\)
\[y = \frac{1}{2}{x^2}.\]
\(y = \frac{1}{4}{x^2}.\)
\(y = 2{x^2}.\)
III. Vận dụng
Cho hàm số \(y = {x^2}\) có đồ thị là \(\left( P \right).\) Đường thẳng đi qua hai điểm thuộc \(\left( P \right)\) có hoành độ bằng \( - 1\) và \(2\) là
\(y = - x + 2.\)
\(y = x + 2.\)
\(y = - x - 2.\)
\(y = x - 2.\)
Khoảng cách giữa hai điểm \(M\left( {{x_1};\,\,{y_1}} \right)\) và \(N\left( {{x_2};\,\,{y_2}} \right)\) được tính công thức:
\(MN = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} .\)
Áp dụng: Cho parabol \(\left( P \right):\,\,y = \frac{1}{2}{x^2}\) cắt đường thẳng \(\left( d \right):\,\,y = x + \frac{3}{2}\) tại hai điểm phân biệt \(A\) và \(B.\) Độ dài đoạn thẳng \(AB\) bằng
\(4\sqrt 2 .\)
\(5\sqrt 3 .\)
\(4.\)
\(2\sqrt 2 .\)
Cho đường thẳng \(\left( d \right):\,\,y = 2x + m\) và parabol \(\left( P \right):\,\,y = {x^2}\,,\) số nguyên \(m\) nhỏ nhất để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt là
\(0.\)
\( - 2.\)
\(1.\)
\(1.\)
Hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) xác định với
mọi giá trị \(x \in \mathbb{R}.\)
mọi giá trị \(x \in \mathbb{Z}.\)
mọi giá trị \(x \in \mathbb{N}.\)
mọi giá trị \(x \in {\mathbb{N}^*}.\)
Điểm đối xứng với điểm \(\left( {x;y} \right)\) qua trục \(Oy\)là
\(\left( {0;0} \right).\)
\(\left( { - x;y} \right).\)
\(\left( {x;y} \right).\)
\[\left( {x; - y} \right).\]
