10 câu hỏi
Đồ thị hàm số y = ax2 (a ≠ 0) có dạng
đường thẳng.
đường gấp khúc.
đường cong parabol.
đường tròn.
Hàm số nào sau đây có dạng y = ax2 (a ≠ 0)?
\[y = {x^2} \cdot \frac{{ - 1}}{2}.\]
\(y = \frac{{{x^2}}}{0}.\)
\(y = \frac{2}{{{x^2}}}.\)
y = 22x.
Cho hàm số y = 3x2. Khẳng định nào sau đây là sai?
Đồ thị hàm số là parabol có đỉnh O.
Đồ thị hàm số nằm phía dưới trục hoành.
Đồ thị hàm số nhận trục Oy làm trục đối xứng.
Đồ thị hàm số đi qua điểm (–1; 3).
Cho các hàm số sau:
(1) y = 2x2;(2) y = –5x2; (3) \(y = \frac{1}{{ - 8}}{x^2};\)(4) \(y = \sqrt {{m^2} + 1} \cdot {x^2}.\)
Có bao nhiêu đồ thị hàm số nằm phía trên trục hoành?
1.
2.
3.
4.
Trong các hàm số sau, hàm số nào có đồ thị nằm phía dưới trục hoành?
y = 8x2.
\(y = \left( {2 - \sqrt 5 } \right){x^2}.\)
\(y = \left( {\sqrt 3 - 1} \right){x^2}.\)
\(y = \left( {2 + \sqrt 3 } \right){x^2}.\)
Trong mặt phẳng tọa độ Oxy, cho hai đồ thị hàm số có dạng như hình vẽ sau:
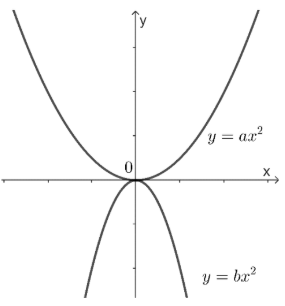
Khẳng định nào sau đây là đúng?
a < 0 < b.
>
a < b < 0.
>
0 < a < b.
>
b < 0 < a.
>
Trong mặt phẳng tọa độ Oxy, cho đồ thị của một hàm số có đồ thị như sau:

y = x2.
y = –x2.
y = 2x2.
y = –2x2.
Để vẽ được đồ thị hàm số \(y = \frac{{ - 1}}{4}{x^2}\) trong mặt phẳng tọa độ Oxy, ta cần xác định các điểm nào sau đây?
(–4; –4); (–2; –1); (0; 0); (2; –1); (4; –4).
(–4; 4); (–2; –1); (0; 0); (2; –1); (4; 4).
(–4; –4); (–2; 1); (0; 0); (2; 1); (4; –4).
(–4; –4); (–2; –1); (0; 0); (2; 1); (4; 4).
Cho hàm số y = (–m2 + 4m – 5)x2. Khi vẽ đồ thị hàm số này trong mặt phẳng tọa độ Oxy thì phần đồ thị mà các giá trị x > 0 nằm ở góc phần tư thứ mấy?
I.
II.
III.
IV.
Khi vẽ đồ thị hàm số \(y = \frac{1}{2}{x^2}\) và y = 2x – 1 trên cùng một mặt phẳng tọa độ Oxy, các giao điểm của hai đồ thị này nằm ở góc phần tư thứ mấy?
I.
II.
III.
IV.
