10 câu hỏi
Đồ thị của hàm số nào sau đây đi qua điểm A(–3; 12)?
\(y = \frac{3}{4}{x^2}.\)
\(y = \frac{4}{3}{x^2}.\)
y = 4x2.
y = 3x2.
Giá trị m > 0 để đồ thị hàm số y = (m2 – 2)x2 đi qua điểm A(1; 2) là
m = 1.
m = 2.
m = 3.
m = 4.
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 3) thuộc đồ thị hàm số y = ax2 (a ≠ 0). Hỏi điểm nào dưới đây thuộc đồ thị hàm số đã cho?
A(2; 12).
B(–2; –12).
C(–3; 12).
D(3; 12).
Giá trị của m để đồ thị hàm số y = (–3m + 1)x2 đi qua điểm A(x; y) với (x; y) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = - 2\\x - 2y = - 3\end{array} \right.\) là
\(m = \frac{1}{3}.\)
\(m = - \frac{1}{3}.\)
m = 3.
m = –3.
Cho hàm số y = ax2 (a ≠0) có đồ thị như hình vẽ sau:
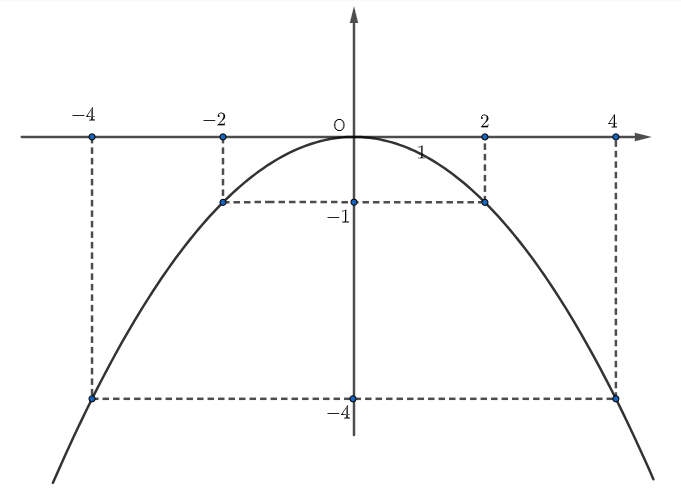
Hệ số a của hàm số trên là
a = –2.
a = 2.
\(a = - \frac{1}{4}.\)
\(a = \frac{1}{4}.\)
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = ax2 (a ≠ 0) và đường thẳng (d): y = 5x – 4. Giá trị của a để đường thẳng (d) cắt (P) tại điểm có hoành độ bằng –2 là
\(a = \frac{7}{2}.\)
\(a = - \frac{7}{2}.\)
\(a = - \frac{1}{{98}}.\)
\(a = \frac{1}{{98}}.\)
Trong mặt phẳng tọa độ Oxy, cho parabol \(\left( P \right):y = \sqrt {5m + 1} \cdot {x^2}\) và đường thẳng (d): y = 5x + 4. Giá trị của m để đường thẳng (d) cắt (P) tại điểm có tung độ bằng 9 là
m = 5.
m = 5.
m = 15.
m = 16.
Hàm số y = (m2 + 3m – 3)x2 (với m2 + 3m – 3 ≠ 0). Tổng các giá trị của m biết đồ thị hàm số đã cho đi qua điểm A(1; 1) là
1.
–1.
–3.
3.
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = ax2 (a ≠ 0) đi qua điểm (–2; –4). Tổng bình phương hoành độ của các điểm trên parabol (P) (khác gốc tọa độ) cách đều hai trục tọa độ là
0.
1.
2.
3.
Trong mặt phẳng tọa độ Oxy, cho parabol \(\left( P \right):y = \left( {\sqrt {3m + 4} - \frac{7}{4}} \right){x^2}\) và đường thẳng (d): y = 3x – 5. Biết đường thẳng (d) cắt parabol (P) tại một điểm có tung độ bằng 1. Hoành độ giao điểm còn lại của đường thẳng (d) và parabol (P) là
2.
–10.
8.
10.
