15 CÂU HỎI
I. Nhận biết
Cho tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\]. Khẳng định nào sau đây là sai?
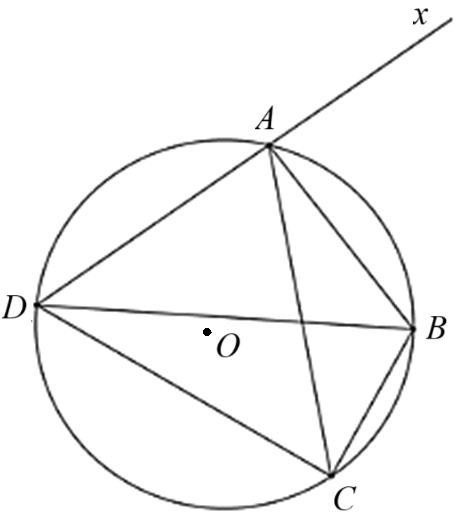
A. \(\widehat {BDC} = \widehat {BAC}\).
B. \(\widehat {BAC} = \widehat {BAx}\).
C. \(\widehat {DCB} = \widehat {BAx}.\)
D. \(\widehat {ABC} + \widehat {ADC} = 180^\circ .\)
Trong các hình dưới đây.
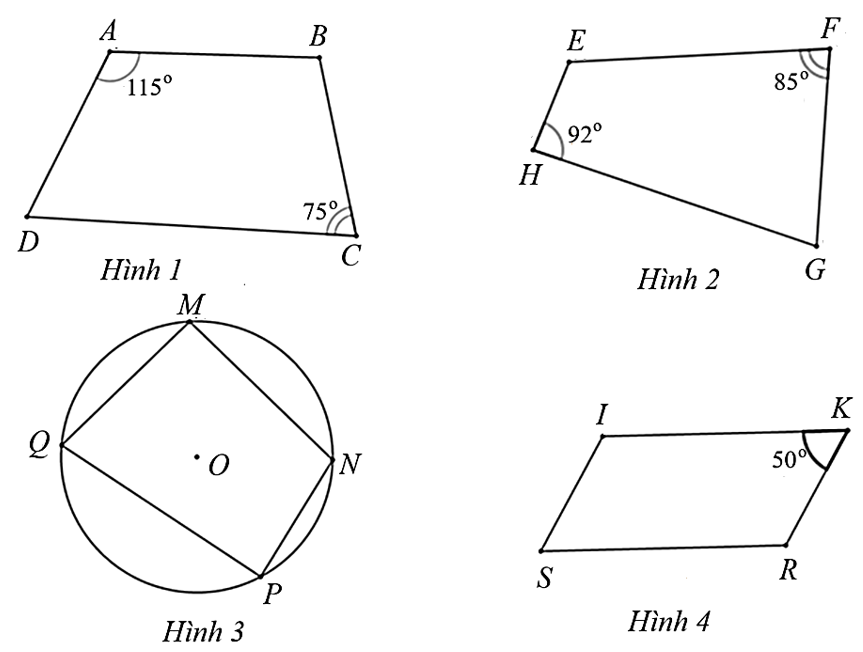
Trong các hình trên, tứ giác trong hình nào là
tứ giác nội tiếp?
D. Hình 4.
A. Hình 1.
B. Hình 2.
C. Hình 3.
Cho nửa đường tròn \[\left( {O;{\rm{ }}R} \right)\] đường kính \[BC\]. Lấy điểm \[A\] trên tia đối của tia \[CB\]. Kẻ tiếp tuyến \[AF,{\rm{ }}Bx\] của nửa kia đường tròn \[\left( O \right)\] (với \[F\] là tiếp điểm). Tia \[AF\] cắt tia \[Bx\] của nửa đường tròn tại \[D\]. Khi đó tứ giác \[OBDF\] là
A. Hình thang.
B. Tứ giác nội tiếp.
C. Hình thang cân.
D. Hình bình hành.
Tứ giác \[ABCD\] nội tiếp đường tròn có hai cạnh đối \[AB\] và \[CD\] cắt nhau tại \[M\] và \(\widehat {BAD} = 70^\circ \) thì số đo góc \[BCM\] là
A. \(110^\circ \).
B. \(30^\circ \).
C. \(70^\circ \).
D. \(55^\circ \).
Cho tam giác \[ABC\] có hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Trong các tứ giác sau, tứ giác nội tiếp là
A. \[AHBC\].
B. \[BCDE\].
C. \[BCDA\].
D. Không có tứ giác nào là tứ giác nội tiếp.
II. Thông hiểu
Cho đường tròn \[\left( O \right)\] có \[AB\] là đường kính. Trên tia đối của tia \[AB\] lấy điểm \[C\] nằm ngoài đường tròn. Lấy điểm \[M\] bất kì nằm trên đường tròn \[\left( O \right)\]. Gọi \[P\] là giao điểm của \[MB\] và đường vuông góc với \[AB\] tại \[C\]. Chọn khẳng định đúng.
A. Tứ giác \[PMAC\] là tứ giác nội tiếp.
B. Tam giác \[BCM\] vuông.
C. Tam giác \[BCP\] có \[CM\] là đường trung tuyến.
D. Không có khẳng định nào đúng.
Cho nửa đường tròn tâm \[O\], đường kính \[AB = 2R\]. Trên tia đối của tia \[AB\] lấy điểm \[E\] (khác với điểm \[A\]). Tiếp tuyến kẻ từ điểm \[E\] cắt các tiếp tuyến kẻ từ điểm \[A\] và \[B\] của nửa đường tròn \[\left( O \right)\] lần lượt tại \[C\] và \[D\]. Gọi \[M\] là tiếp điểm của tiếp tuyến kẻ từ điểm \[E\]. Trong các khẳng định sau, khẳng định nào là sai?
A. Tứ giác \[OACM\] là tứ giác nội tiếp.
B. Tứ giác \[OBDM\] là tứ giác nội tiếp.
C. Tứ giác \[ACDB\] là hình thang vuông.
D. Tứ giác \[ACDB\] là tứ giác nội tiếp.
Cho tứ giác \[ABCD\] có số đo các góc \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] tương ứng. Trường hợp nào sau đây thì tứ giác \[ABCD\] có thể là tứ giác nội tiếp?
A. \(50^\circ \,;\,\,60^\circ \,;\,\,130^\circ \,;\,\,140^\circ \).
B. \(65^\circ \,;\,\,85^\circ \,;\,\,115^\circ \,;\,\,95^\circ .\)
C. \(82^\circ \,;\,\,90^\circ \,;\,\,98^\circ \,;\,\,100^\circ .\)
D. Không có trường hợp nào .
Cho tam giác \[ABC\] vuông tại \[A\] đường cao \[AH\]. Kẻ \[HE\] vuông góc với \[AB\] tại \[E\], kẻ \[HF\] vuông góc với \[AC\] tại \[F\]. Chọn câu đúng:
A. Tứ giác \[BEFC\] là tứ giác nội tiếp.
B. Tứ giác \[BEFC\] không nội tiếp.
C. Tứ giác \[AFHE\] là hình vuông.
D. Tứ giác \[AFHE\] không nội tiếp.
Cho điểm \[A\] nằm ngoài đường tròn \[\left( O \right)\] qua \[A\] kẻ hai tiếp tuyến \[AB\] và \[AC\] với đường tròn (\[B,{\rm{ }}C\] là tiếp điểm). Chọn đáp án đúng:
A. Tứ giác \[ABOC\]là hình thoi.
B. Tứ giác \[ABOC\] nội tiếp.
C. Tứ giác \[ABOC\] không nội tiếp.
D. Tứ giác \[ABOC\] là hình bình hành.
Cho hình vẽ dưới đây:
![Cho hình vẽ dưới đây:Số đo góc \[ABC\] là (ảnh 1)](https://video.vietjack.com/upload2/images/1731762517/1731763236-image10.png)
Số đo góc \[ABC\] là
A. \(80^\circ \).
B. \(90^\circ \).
C. \(100^\circ \).
D. \(110^\circ \).
Cho đường tròn \[\left( O \right)\] đường kính \[AB\]. Gọi \[H\] là điểm nằm giữa \[O\] và \[B\]. Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H\]. Trên cung nhỏ \[AC\] lấy điểm \[E\], kẻ \[CK \bot AE\] tại \[K\]. Đường thẳng \[DE\] cắt \[CK\] tại \[F\]. Khẳng định nào sau đây là đúng?
A. Tứ giác \[AHCK\] là tứ giác nội tiếp.
B. Tứ giác \[AHCK\] là hình bình hành.
C. Tứ giác \[AHCK\] là hình thang.
D. Tứ giác \[AHCK\] là hình thoi.
III. Vận dụng
Cho đường tròn \[\left( O \right)\] đường kính \[AB\]. Gọi \[H\] là điểm nằm giữa \[O\] và \[B\]. Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H\]. Trên cung nhỏ \[AC\] lấy điểm \[E\], kẻ \[CK \bot AE\] tại K. Đường thẳng \[DE\] cắt \[CK\] tại \[F\]. Tích \[AH.{\rm{ }}AB\] bằng
A. \(4A{O^2}\).
B. \(AD \cdot BD\).
C. \(B{D^2}\).
D. \(A{D^2}\).
Cho đường tròn \[\left( O \right)\] đường kính \[AB\]. Gọi \[H\] là điểm nằm giữa \[O\] và \[B\]. Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H\]. Trên cung nhỏ \[AC\] lấy điểm \[E\], kẻ \[CK \bot AE\] tại \[K\]. Đường thẳng \[DE\] cắt \[CK\] tại \[F\]. Tam giác \[ACF\] là tam giác
A. cân tại \[F\].
B. cân tại \[C\].
C. cân tại \[A\].
D. đều.
Cho hình bình hành \[ABCD\]. Đường tròn đi qua ba đỉnh \[A,{\rm{ }}B,{\rm{ }}C\] cắt đường thẳng \[CD\] tại \[P\] (điểm \[P\] khác với điểm \[C\]). Khi đó
A. \[ABCP\] là hình thang cân.
B. \[AP = AD\].
C. \[AP = BC\].
D. Cả A, B, C đều đúng.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
