15 CÂU HỎI
I. Nhận biết
Tâm đối xứng của đường tròn là
A. Điểm bất kì bên trong đường tròn.
B. Điểm bất kì bên ngoài đường tròn.
C. Điểm bất kì trên đường tròn.
D. Tâm của đường tròn.
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng.
C. Đường tròn có hai trục đối xứng là hai đường thẳng đi qua tâm và vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng.
Cho đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và một điểm \[K\] bất kì. Biết rằng \[OK = 7{\rm{\;cm}}.\] Khẳng định nào sau đây đúng?
A. Điểm \[K\] nằm trong đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
B. Điểm \[K\] nằm ngoài đường tròn
C. Điểm \[K\] nằm trên đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
D. Điểm \[K\] thuộc đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
Cho đường tròn \[\left( O \right)\] đường kính \[AB\] và dây \[CD\] không đi qua tâm. Khẳng định nào sau đây là đúng?
A.
B. \[AB > CD.\]
C. \[AB = CD.\]
D. \[AB \ge CD.\]
Cho hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] với \[R > r\] cắt nhau tại hai điểm phân biệt và \[OO' = d.\] Chọn khẳng định đúng?
A. \[d > R + r.\]
B. \[d = R - r.\]
C. \[d < R - r.\]
D. \[R - r < d < R + r.\]
II. Thông hiểu
Cho hình chữ nhật \[ABCD\] có \[AC = 16{\rm{\;cm}}.\] Biết rằng bốn điểm \[A,B,C,D\] cùng thuộc một đường tròn. Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD.\] Tâm và bán kính của đường tròn đó là
A. Tâm \[D,\] bán kính \[R = 16{\rm{\;cm}}.\]
B. Tâm \[O,\] bán kính \[R = 16{\rm{\;cm}}.\]
C. Tâm \[O,\] bán kính \[R = 8{\rm{\;cm}}.\]
D. Tâm \[O,\] bán kính \[R = 4{\rm{\;cm}}.\]
Cho đường tròn \[\left( O \right)\] có bán kính \[R = 5{\rm{\;cm}}.\] Khoảng cách từ tâm đến dây \[AB\] là \[3{\rm{\;cm}}.\] Độ dài dây \[AB\] bằng
A. \[4{\rm{\;cm}}.\]
B. \[6{\rm{\;cm}}.\]
C. \[8{\rm{\;cm}}.\]
D. \[12{\rm{\;cm}}.\]
Cho hai đường tròn \(\left( O \right)\) đường kính \(7{\rm{\;cm}}\) và \(\left( {I;\,4{\rm{\;cm}}} \right).\) Biết \(OI = 1{\rm{\;cm,}}\) vị trí tương đối của hai đường tròn \(\left( O \right)\) và \(\left( I \right)\) là
A. tiếp xúc trong.
B. \(\left( I \right)\) đựng \(\left( O \right).\)
C. cắt nhau.
D. \(\left( O \right)\) đựng \(\left( I \right).\)
Cho hai đường tròn \(\left( {O;1{\rm{\;cm}}} \right)\) và \(\left( {I;3{\rm{\;cm}}} \right)\) cắt nhau, đoạn thẳng \(OI\) có độ dài là
A. \(2{\rm{\;cm}}\).
B. \(3{\rm{\;cm}}{\rm{.}}\)
C. \(4{\rm{\;cm}}\).
D. \(5{\rm{\;cm}}.\)
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\) với \(R < 5{\rm{\;cm}}.\) Biết \(OI = 3{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn tiếp xúc trong là
A. \(1{\rm{\;cm}}{\rm{.}}\)
B. \(2{\rm{\;cm}}.\)
C. \(4{\rm{\;cm}}.\)
D. \(8{\rm{\;cm}}.\)
Cho hai đường tròn \[\left( {O;5{\rm{\;cm}}} \right)\] và \(\left( {I;R} \right)\). Biết \(OI = 7{\rm{\;cm}},\) giá trị của \(R\) để hai đường tròn ở ngoài nhau là
A. \(1{\rm{\;cm}}{\rm{.}}\)
B. \(2{\rm{\;cm}}.\)
C. \(6{\rm{\;cm}}.\)
D. \({\rm{12\;cm}}.\)
Cho đường tròn \(\left( {I;R} \right)\) có đường kính \[12{\rm{\;dm}}\] và đường tròn \(\left( {J;R'} \right)\) có đường kính \[18{\rm{\;dm}}.\] Nếu \(IJ = 15{\rm{\;dm}}\) thì hai đường tròn \[\left( I \right),\,\,\left( J \right)\] có vị trí tương đối là
A. tiếp xúc trong.
B. tiếp xúc ngoài.
C. ở ngoài nhau.
D. đựng nhau.
III. Vận dụng
Cho đường tròn \[\left( {O;R} \right)\] có hai dây \[AB,CD\] vuông góc với nhau tại \[M.\] Giả sử \[AB = 16{\rm{\;cm}},CD = 12{\rm{\;cm}},MC = 2{\rm{\;cm}}.\] Kẻ \[OH \bot AB\] tại \[H,\] \[OK \bot CD\] tại \[K.\] Khi đó diện tích tứ giác \[OHMK\] bằng
A. \[2 + \sqrt {11} {\rm{\;c}}{{\rm{m}}^2}.\]
B. \[4 + 2\sqrt {11} {\rm{\;c}}{{\rm{m}}^2}.\]
C. \[8\sqrt {11} {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[4\sqrt {11} {\rm{\;c}}{{\rm{m}}^2}.\]
Trong một trò chơi, hai bạn Thủy và Tiến cùng chạy trên một đường tròn tâm \[O\] có bán kính \[20{\rm{\;m}}\] (hình vẽ).
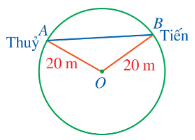
Độ dài dây \[AB\] nối vị trí của hai bạn đó không thể bằng bao nhiêu mét?
A. \[38{\rm{\;m}}.\]
B. \[39{\rm{\;m}}.\]
C. \[40{\rm{\;m}}.\]
D. \[41{\rm{\;m}}.\]
Cho hai đường tròn \[\left( {O;4{\rm{\;cm}}} \right)\] và \[\left( {O';3{\rm{\;cm}}} \right)\] biết \[OO' = 5{\rm{\;cm}}.\] Hai đường tròn trên cắt nhau tại \[A\] và \[B.\] Độ dài \[AB\] là
A. \[5{\rm{\;cm}}.\]
B. \[2,4{\rm{\;cm}}.\]
C. \[4,8{\rm{\;cm}}.\]
D. \[9,6{\rm{\;cm}}.\]
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
