15 CÂU HỎI
Cho phương trình \(a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\) có \(\Delta = {b^2} - 4ac.\) Khẳng định nào sau đây là đúng
A. Phương trình có hai nghiệm phân biệt khi \(\Delta > 0\); phương trình vô nghiệm khi \(\Delta = 0.\)
B. Phương trình có hai nghiệm phân biệt khi \(\Delta > 0\); phương trình có nghiệm kép khi \(\Delta = 0.\)
C. Phương trình có nghiệm phân biệt khi \(\Delta \ge 0\); phương trình vô nghiệm khi \(\Delta = 0.\)
D. Phương trình có hai nghiệm phân biệt khi \(\Delta = 0\); phương trình vô nghiệm khi \(\Delta < 0.\)
>
Nếu phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\)có hai nghiệm \({x_1};\,{x_2}\) thì
A. \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\)B. \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\)C. \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{b}{a}\\{x_1}{x_2} = \frac{a}{c}\end{array} \right..\)D. \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{b}{a}\\{x_1}{x_2} = - \frac{c}{a}\end{array} \right..\)
Hướng dẫn giải
Đáp án đúng là: B
Định lí Viète: Nếu \({x_1};\,{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) thì
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right..\)Câu 4. Nếu hai số \(x;\,y\) có \(x + y = S\) và \(xy = P\) (điều kiện \({S^2} - 4P \ge 0\)) thì \(x;\,y\) là hai nghiệm của phương trình
A. \({x^2} + Sx + P = 0.\)
B. \({x^2} - Sx + P = 0.\)
C. \({x^2} + Sx - P = 0.\)
D. \({x^2} - Sx - P = 0.\)
Một hình chữ nhật có chiều dài gấp \(3\) lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm \(5\) cm thì được một hình chữ nhật mới có diện tích bằng \(153\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\) Nếu gọi chiều rộng của hình chữ nhật là \(x\)(cm) với \(x > 0\) và chiều dài của hình chữ nhật là \(3x\) cm. Khi đó, chiều rộng và chiều dài hình chữ nhật sau khi tăng thêm lần lượt là là \(x + 5\) (cm) và \(3x + 5\) (cm). Phương trình của bài toán để tính chu vi hình chữ nhật ban đầu là
A. \(\left( {x + 5} \right)\left( {3x + 5} \right) = 153.\)
B. \(\left( {x - 5} \right)\left( {3x + 5} \right) = 153.\)
C. \(\left( {x + 5} \right)\left( {3x - 5} \right) = 153.\)
D. \(\left( {x + 5} \right)\left( {3 - x} \right).5 = 153.\)
II. Thông hiểu
Cho hàm số bậc hai \(y = 4{x^2}.\) Giá trị của \(y\) khi \(x = - 2\) là
A. \(y = - 16.\)
B. \(y = 4.\)
C. \(y = 16.\)
D. \(y = - 4.\)
Cho đồ thị của một hàm số bậc hai sau:
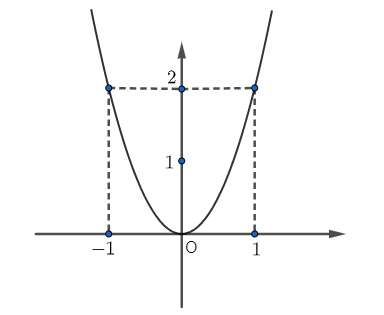
Hệ số \(a\) của đồ thị hàm số bậc hai này là
A. \(a = - 1.\)
B. \(a = 1.\)
C. \(a < 0.\)
>
D. \(a > 0.\)
Cho phương trình \(2{x^2} + 2\sqrt {11} x + 3 = 0.\) Khẳng định nào sau đây là đúng
A. Phương trình có hai nghiệm phân biệt.
B. Phương trình vô nghiệm.
C. Phương trình có nghiệm kép.
D. Phương trình có vô số nghiệm
Tìm nghiệm của phương trình \(2{x^2} - 2\sqrt 5 x + 1 = 0.\)
A. \({x_1} = \frac{{2\sqrt 5 + \sqrt 3 }}{2};\,\,{x_2} = \frac{{2\sqrt 5 - \sqrt 3 }}{2}.\)
B. \({x_1} = \frac{{\sqrt 5 + \sqrt 3 }}{2};\,\,{x_2} = \frac{{\sqrt 5 - \sqrt 3 }}{2}.\)
C. \({x_1} = {x_2} = \frac{{\sqrt 5 }}{2}.\)
D. \({x_1} = \sqrt 5 + \sqrt 3 ;\,\,{x_2} = \sqrt 5 - \sqrt 3 .\)
Cho \(x;\,y\) là hai nghiệm của phương trình \(2{x^2} + 2\sqrt 2 x + 4 = 0.\) Tìm tổng hai nghiệm và tích hai nghiệm của phương trình
A. \(x + y = 2\sqrt 2 ;\,xy = 2.\)
B. \(x + y = - \sqrt 2 ;\,xy = - 2.\)
C. \(x + y = - \sqrt 2 ;\,xy = 2.\)
D. \(x + y = \sqrt 2 ;\,xy = 2.\)
Phương trình \(m{x^2} + 2\left( {m + 1} \right)x - 1 = 0\) có hai nghiệm trái dấu khi
A. \(m > 0.\)
B. \(m < 0.\)
>
C. \(m = 0.\)
D. \(m \ne 0.\)
Cho quãng đường từ địa điểm A đến địa điểm B là \(90\) km. Lúc 6 giờ, một xe máy đi từ A để tới B. Lúc 6 giờ 30 phút cùng ngày, một ô tô cũng đi từ A để tới B với vận tốc lớn hơn vận tốc xe máy \(15\) km/h (Hai xe chạy trên cùng một con đường đã cho). Hai xe nói trên đều đến B cùng lúc. Phương trình của bài toán để tính vận tốc của xe máy là
A. \(\frac{{90}}{x} + \frac{1}{2} = \frac{{90}}{{x + 15}}.\)
B. \(\frac{{90}}{x} - \frac{1}{2} = \frac{{90}}{{x + 15}}.\)
C. \(\frac{1}{2} - \frac{{90}}{x} = \frac{{90}}{{x + 15}}.\)
D. \(\frac{{90}}{x} + \frac{{90}}{{x + 15}} = \frac{1}{2}.\)
III. Vận dụng
Cho phương trình \({x^2} - 4mx + 4{m^2} - 2 = 0\,\,\,\left( 1 \right)\) có hai nghiệm phân biệt là \({x_1};\,\,{x_2}\). Giá trị của biểu thức \(P = x_1^2 + 4m{x_2} - 12{m^2} - 6\) là
A. \( - 4.\)
B. \(3.\)
C. \( - 6.\)
D. \(5.\)
Giá trị của \(m\) để phương trình \({x^2} + 2mx + 4 = 0\) có hai nghiệm \({x_1},\,{x_2}\) thỏa mãn \(\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = 3\) là
A. \(m = - \sqrt 5 .\)
B. \(m = \sqrt 5 .\)
C. \[m = \sqrt 3 .\] và \(m = \sqrt 3 .\)
D. \(m = \sqrt 5 \) và \[m = - \sqrt 5 \] .
I. Nhận biết
Cho hai đường parabol trong mặt phẳng tọa độ \[{\rm{Ox}}y.\] Khẳng định nào sau đây là đúng?
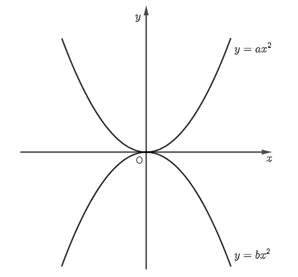
A.\(a < 0 < b.\)
B.\(a < b < 0.\)
C.\(a > b > 0.\)
D. \(a > 0 > b.\)
Nếu hai số \(x;\,y\)có \(x + y = S\) và \(xy = P\) (điều kiện \({S^2} - 4P \ge 0\)) thì \(x;\,y\) là hai nghiệm của phương trình
A.\({x^2} + Sx + P = 0.\)
B. \({x^2} - Sx + P = 0.\)
C. \({x^2} + Sx - P = 0.\)
D. \({x^2} - Sx - P = 0.\)
Hưởng ứng phong trào “Vì biển đảo Trường Sa”, một đội tàu dự định chở \(280\) tấn hàng ra đảo. Nhưng khi chuẩn bị khởi hành thì số hàng hóa đã tăng thêm \(6\) tấn so với dự định. Vì vậy đội tài phải bổ sung thêm \(1\) tàu và mỗi tàu chở ít hơn dự định \(2\) tấn hàng. Hỏi khi dự định, đội tài có bao nhiêu chiếc tàu, biết các tàu chở số tấn hàng bằng nhau?
A. \(5.\)
B. \(6.\)
C. \(1.\)
D. \(7.\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải