15 CÂU HỎI
I. Nhận biết
Cho hình vẽ dưới đây.
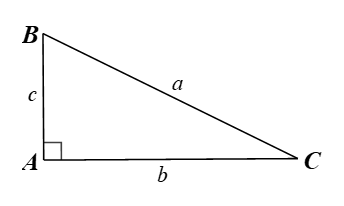
Hệ thức nào sau đây đúng?
A. \[c = a.\cot B.\]
B. \[c = a.\sin B.\]
C. \[c = a.\tan B.\]
D. \[c = a.\cos B.\]
Cho hình vẽ dưới đây.
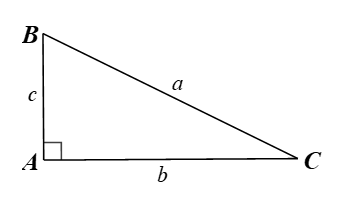
Hệ thức nào sau đây đúng?
A. \[c = b\cot B.\]
B. \[b = a\tan C.\]
C. \[b = c\tan C.\]
D. \[c = a\tan B.\]
Bài toán “giải tam giác vuông” là
A. Bài toán tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.
B. Bài toán tìm ít nhất độ dài một cạnh và tất cả số đo các góc còn lại của tam giác đó.
C. Bài toán tìm tất cả độ dài các cạnh và số đo của một góc bất kì của tam giác đó.
D. Bài toán tìm độ dài một cạnh và số đo của một góc của tam giác đó.
Nếu tam giác \[MNP\] vuông tại \[M\] có \[NP = 5,\,\,\cos N = \frac{3}{5}\] thì \[MN\] bằng
A. \[3.\]
B. \[4.\]
C. \[\frac{3}{{25}}.\]
D. \[\frac{{25}}{3}.\]
Cho hình vẽ dưới đây.
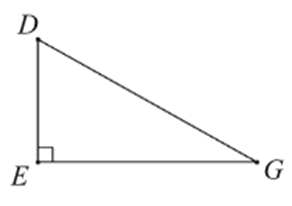
Hệ thức nào sau đây sai?
A. \[DG = \frac{{EG}}{{\sin D}}.\]
B. \[DG = \frac{{DE}}{{\sin G}}.\]
C. \[DG = \frac{{EG}}{{\cos G}}.\]
D. \[DG = \frac{{EG}}{{\cot G}}.\]
II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 10{\rm{\;cm}},\,\,\widehat C = 30^\circ .\] Độ dài cạnh \[AB\] bằng
A. \[\frac{{5\sqrt 3 }}{3}\] (cm).
B. \[\frac{{10\sqrt 3 }}{3}\] (cm).
C. \[5\sqrt 3 \] (cm).
D. \[10\sqrt 3 \] (cm).
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng
A. \[40\] (cm).
B. \[40\sqrt 3 \] (cm).
C. \[20\sqrt 3 \] (cm).
D. \[20\] (cm).
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 12{\rm{\;cm}},\,\,\widehat B = 40^\circ .\] Kết quả nào sau đây là đúng?
A. \[AC \approx 9,19\,\,{\rm{cm}};\,\,\widehat {C\,} = 50^\circ.\]
B. \[AC \approx 7,71{\rm{\;cm}};\,\,\widehat {C\,} = 50^\circ.\]
C. \[AC \approx 9,1\,\,{\rm{cm}};\,\,\widehat {C\,} = 50^\circ.\]
D. \[AC \approx 7,8{\rm{\;cm}};\,\,\widehat {C\,} = 50^\circ.\]
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 15{\rm{\;cm}},\,\,AB = 12{\rm{\;cm}}.\] Kết quả nào sau đây là đúng?
A. \[AC = 9{\rm{\;cm}};\,\,\widehat {B\,} \approx 36^\circ 53'.\]
B. \[AC = 9{\rm{\;cm}};\,\,\widehat {B\,} \approx 53^\circ 8'.\]
C. \[AC = 9{\rm{\;cm}};\,\,\widehat {B\,} \approx 36^\circ 52'.\]
D. \[AC = 9{\rm{\;cm}};\,\,\widehat {B\,} \approx 53^\circ 7'.\]
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm,}}\,\,AC = 7{\rm{\;cm}}{\rm{.}}\] Kết quả nào sau đây là đúng?
A. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 35^\circ 32'.\]
B. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
C. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat {C\,} \approx 35^\circ 32'.\]
D. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 6{\rm{\;cm}},\,\,\tan B = \frac{5}{{12}}.\] Kết quả nào sau đây là đúng?
A. \[AC = 5\] cm; \[BC = 13\] cm.
B. \[AC = 13\] cm; \[BC = 5\] cm.
C. \[AC = 6,5\] cm; \[BC = 2,5\] cm.
D. \[AC = 2,5\] cm; \[BC = 6,5\] cm.
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 16{\rm{\;cm}},\,\,\sin B = \frac{3}{5}.\] Kết quả nào sau đây là sai?
A. \(\cos C = \frac{3}{5}.\)
B. \(\cos B = \frac{4}{5}.\)
C. \[BC = 26,6\] cm.
D. \[AB = 21,3\] cm.
III. Vận dụng
Cho tam giác \[ABC\] nhọn có \[AB = 3,5;\,\,AC = 4;\,\,\widehat {A\,} = 40^\circ \] và \[BH\] là đường cao. Diện tích tam giác \[ABC\] gần nhất với
A. \[5\] (đvdt).
B. \[4,5\] (đvdt).
C. \[3\] (đvdt).
D. \[3,5\] (đvdt).
Cho tam giác \[ABC\] có \[BC = 9{\rm{\;cm}},\,\,\widehat {ABC} = 50^\circ \] và \[\widehat {ACB} = 35^\circ .\] Gọi \[N\] là chân đường vuông góc hạ từ \[A\] xuống cạnh \[BC.\] Độ dài \[AN\] gần nhất với giá trị nào dưới đây?
A. \[2{\rm{\;cm}}.\]
B. \[3{\rm{\;cm}}.\]
C. \[4{\rm{\;cm}}.\]
D. \[5{\rm{\;cm}}.\]
Cho hình thang \[ABCD\] có \[\widehat {A\,} = \widehat {D\,} = 90^\circ ,\,\,\widehat {C\,} = 50^\circ .\] Biết rằng \[AB = 2;\,\,AD = 1,2.\] Khi đó diện tích hình thang \[ABCD\] gần nhất với
A. \[5\] (đvdt).
B. \[4\] (đvdt).
C. \[3\] (đvdt).
D. \[2\] (đvdt).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
