Quiz

15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 6: Tính chất ba đường trung trực của tam giác có đáp án

Admin15 câu hỏiToánLớp 7

Bắt đầu ngay

15 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Điền vào chỗ trống sau: “Trong một tam giác, đường trung trực của mỗi cạnh gọi là … của tam giác đó”.

A. Đường trung tuyến;

B. Đường trung trực;

C. Trọng tâm;

D. Trung điểm.

2. Nhiều lựa chọn

Điền vào chỗ trống sau: “Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này … ba đỉnh của tam giác đó.”

A. Giao;

B. Nằm trên;

C. Cách đều;

D. Thuộc.

3. Nhiều lựa chọn

Cho tam giác ABC có M và N lần lượt là trung điểm của AB, BC. Từ M, N vẽ hai đường trung trực cắt nhau tại O. Cho OA= 5 cm. Độ dài đoạn thẳng OB bằng:

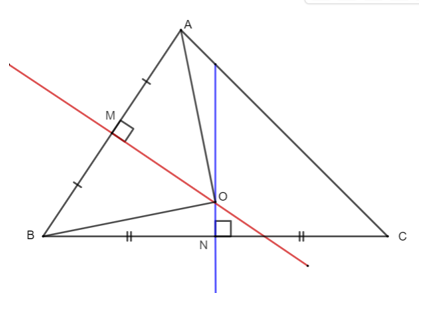
Cho tam giác ABC có M và N lần lượt là trung điểm của AB, BC. Từ M, N (ảnh 1)

A. 4 cm;

B. 5 cm;

C. 10 cm;

D. 20 cm.

4. Nhiều lựa chọn

Gọi O là giao điểm của ba đường trung trực trong ∆ABC. Khi đó điểm O là:

A. Trọng tâm của ∆ABC;

B. Điểm cách đều ba cạnh của ∆ABC;

C. Điểm cách đều ba đỉnh của ∆ABC;

D. Tất cả các đáp án trên đều sai.

5. Nhiều lựa chọn

Cho tam giác ABC cân tại A có góc $\hat{B A C}$ = 60° có AH là đường cao và K là trung điểm của AC. Từ K kẻ đường trung trực của AC cắt AH tại O . Số đo góc OCA là:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

6. Nhiều lựa chọn

Quan sát hình bên dưới, cho biết OA = 8cm. Độ dài đoạn thẳng OC bằng:

Quan sát hình bên dưới, cho biết OA = 8cm. Độ dài đoạn thẳng OC bằng: (ảnh 1)

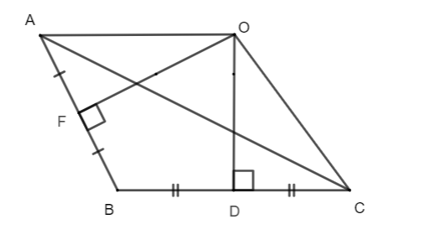
A. 8

B. 16

C. 4

D. 2

7. Nhiều lựa chọn

Cho tam giác ∆ABC vuông cân tại A có H và K lần lượt là trung điểm của hai cạnh AB và AC. Từ H và K kẻ đường trung trực của hai cạnh AB và AC cắt nhau tại O. Tính số đo $\hat{O A C}$ .

A. 30°;

B. 45°;

C.60°;

D.90°.

8. Nhiều lựa chọn

Cho tam giác ∆ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn câu đúng:

A. ∆AOB = ∆COE;

B. ∆ABO = ∆CEO;

C. ∆ABE = ∆CDE;

D. ∆ABO = ∆COE.

9. Nhiều lựa chọn

Cho tam giác ∆ABC có $\hat{A}$ là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và đường trung trực của AB cắt BC tại E. Khi đó, ∆EAB là:

A.Tam giác thường;

B. Tam giác vuông;

C. Tam giác đều;

D. Tam giác cân.

10. Nhiều lựa chọn

Cho tam giác ∆ABC có $\hat{A}$ là góc tù. Các đường trung trực của AB và AC cắt nhau tại O. Đường tròn tâm O bán kính OA đi qua điểm:

A. B và C;

B. M và N;

C. B

D. C

11. Nhiều lựa chọn

Cho tam giác ∆ABC cân tại A, có M là trung điểm của BC. Đường trung trực của AB cắt AM tại O. Khi đó điểm O:

A. Là trọng tâm của ∆ABC;

B. Cách đều ba cạnh của ∆ABC;

C. Là trực tâm của ∆ABC

D.Cách đều ba đỉnh của ∆ABC.

12. Nhiều lựa chọn

Cho ∆ABC, P là trung điểm của AC. Các đường trung trực của AB và BC cắt nhau tại O. Số đo bằng $\hat{O P C}$ :

A. 30°;

B. 60°;

C. 90°;

D. 45°.

13. Nhiều lựa chọn

Cho tam giác ∆ABC có M và N lần lượt là trung điểm của AB, BC. Từ M và N vẽ 2 đường trung trực cắt nhau tại O. Biết đường tròn tâm O bán kính OA có đường kính bằng 8 cm. Độ dài đoạn thẳng OB bằng:

A. 2 cm;

B. 4 cm;

C. 8 cm;

D. 5 cm.

14. Nhiều lựa chọn

Một điểm được gọi là cách đều ba đỉnh của một tam giác khi là:

A. Giao điểm của ba đường cao của tam giác;

B. Giao điểm của ba đường trung trực của tam giác;

C. Trọng tâm của tam giác;

D. Trực tâm của tam giác.

15. Nhiều lựa chọn

Giao điểm O của ba đường trung trực của tam giác thuộc: