15 câu hỏi
Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \) với số thực k như thế nào thì vectơ \(k\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow a \).
k = 1;
k = 0;
k < 0;
k > 0.
Cho vectơ \(\overrightarrow a \), \(\overrightarrow b \) và hai số thực k, t. Khẳng định nào sau đây là sai?
k(t\(\overrightarrow a \)) = (kt)\(\overrightarrow a \);
(k + t)\(\overrightarrow a \) = k\(\overrightarrow a \) + t\(\overrightarrow b \);
k\(\left( {\overrightarrow a + \overrightarrow b } \right)\) = k\(\overrightarrow a \) + k\(\overrightarrow b \);
(-1)\(\overrightarrow a \) = -\(\overrightarrow a \).
Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \).Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
k < 0
k = 1
0 < k < 1
k > 1
Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
K là trung điểm của AB
K là điểm nằm giữa I và A thỏa mãn IK = \(\frac{1}{3}\) IB với I là trung điểm của AB.
K là điểm nằm giữa I và B thỏa mãn IK = \(\frac{1}{3}\) IB với I là trung điểm của AB.
K là điểm nằm giữa I và A thỏa mãn IK = \(\frac{1}{3}\) IA với I là trung điểm của AB.
Cho tam giác ABC có đường trung tuyến AM. Khi đó \(\overrightarrow {AM} = a\overrightarrow {AB} + b\overrightarrow {AC} \). Tính S = a + 2b.
1;
2;
\(\frac{1}{2}\);
\(\frac{3}{2}.\)
Các tam giác ABC có trọng tâm G; M, N lần lượt là trung điểm của BC và AB. Biểu thị \(\overrightarrow {MG} \) thông qua hai vec tơ \(\overrightarrow {AB} ,\overrightarrow {AC} \).
\(\overrightarrow {NG} = - \frac{1}{6}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} \);
\(\overrightarrow {NG} = - \frac{1}{6}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \);
\(\overrightarrow {NG} = - \frac{1}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \);
\(\overrightarrow {NG} = - \frac{1}{6}\overrightarrow {AC} + \frac{2}{3}\overrightarrow {AB} \).
Cho tam giác ABC có G là trọng tâm tam giác. Hãy xác định điểm M để \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
M là trung điểm của đoạn thẳng GC;
M nằm giữa G và C sao cho GM = 4GC;
M nằm ngoài G và C sao cho GM = 4GC;
M nằm giữa G và C sao cho \(GM = \frac{1}{4}GC\).
Trong hình vẽ, hãy biểu thị mỗi vectơ \(\overrightarrow u ,\overrightarrow v \)hai vectơ \(\overrightarrow a ,\overrightarrow b \), tức là tìm các số x, y, z, t để \(\overrightarrow u = x\overrightarrow a + y\overrightarrow b ,\overrightarrow v = t\overrightarrow a + z\overrightarrow b .\)
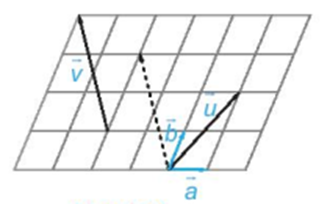
x = 1, y = 2, z = 2, t = -1;
x = 1, y = 2, z = -2, t = 3;
x = 1, y = 2, z = -2, t = -1;
x = 1, y = -2, z = 2, t = -3.
Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = \[\frac{1}{3}\]AC. Hãy xác định điểm M để \(\overrightarrow {MA} + 3\overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
M là trung điểm BC;
M là đỉnh hình chữ nhật AEFM;
M là đỉnh hình bình hành EAFM;
M là đỉnh tam giác đều BEM.
Biết rằng hai vectơ \(\overrightarrow a \)và \(\overrightarrow b \) không cùng phương nhưng hai vectơ \(5x\overrightarrow a + 4\overrightarrow b \) và \(\left( {3x - 2} \right)\overrightarrow a - 2\overrightarrow b \)cùng phương. Khi đó giá trị của x bằng:
\(\frac{4}{{11}}\);
\(\frac{2}{3}\);
4;
-4.
Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)như hình vẽ và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.
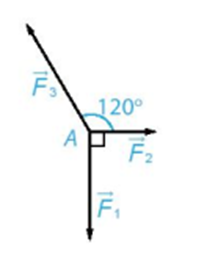
\(\left| {\overrightarrow {{F_1}} } \right| = \frac{{20}}{{\sqrt 3 }}N,\left| {\overrightarrow {{F_2}} } \right| = \frac{{40\sqrt 3 }}{3}N;\)
\(\left| {\overrightarrow {{F_1}} } \right| = \frac{{40}}{{\sqrt 3 }}N,\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3}N;\)
\(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \frac{{40\sqrt 3 }}{3}N;\)
\(\left| {\overrightarrow {{F_1}} } \right| = \frac{{60}}{{\sqrt 3 }}N,\left| {\overrightarrow {{F_2}} } \right| = \frac{{40\sqrt 3 }}{3}N.\)
Cho hình vuông ABCD có cạnh AB = 2 và giao điểm các đường chéo là H. Tính độ dài của vectơ \(\overrightarrow {AB} + 2\overrightarrow {AH} \).
\(\frac{{\sqrt 2 }}{2}\)
\(\frac{{\sqrt 3 }}{2}\)
\(\sqrt 5 \)
\(\frac{1}{2}\)
Cho tứ giác ABCD. Gọi M là trung điểm của cạnh AB, CD. Đẳng thức nào dưới đây là sai?
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {MN} \);
\(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} \);
\[\overrightarrow {BC} + \overrightarrow {AD} = 3\overrightarrow {MN} \];
\(\overrightarrow {BC} + \overrightarrow {AD} = 4\overrightarrow {MN} \).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?
\(2\overrightarrow a + \overrightarrow b \) và \(\frac{1}{3}\overrightarrow a - \frac{1}{2}\overrightarrow b \);
\( - \overrightarrow a + \overrightarrow b \) và \( - 2\overrightarrow a + 3\overrightarrow b \);
\(\frac{1}{6}\overrightarrow a - \overrightarrow b \) và \( - \overrightarrow a + 6\overrightarrow b \);
\(\overrightarrow a + \overrightarrow b \) và \(\overrightarrow a - \overrightarrow b \).
Cho hình vẽ sau:
Phát biểu nào dưới đây là đúng?
\(5\overrightarrow {MP} = 4\overrightarrow {MN} \);
\(\overrightarrow {PM} = 4\overrightarrow {PN} \);
\(\overrightarrow {PN} = - \frac{1}{5}\overrightarrow {MN} \);
Cả A, B và C đều sai
Gợi ý cho bạn
Xem tất cả10 Bài tập Chứng minh ba điểm thẳng hàng (có lời giải)
10 Bài tập Chứng minh hai vectơ cùng phương (có lời giải)