14 bài tập Giải toán liên quan đến tỉ lệ diện tích tam giác có lời giải

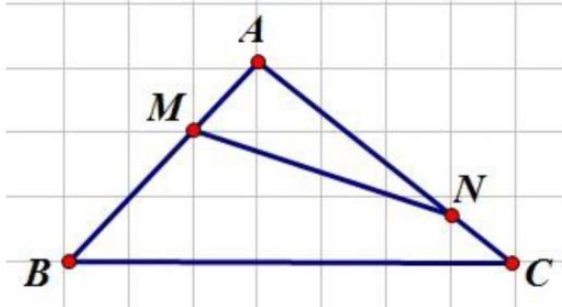
Một hình tam giác ABC có D là điểm chính giữa của BC, E là điểm chính giữa của CA, AD cắt BE ở G. Hãy chứng tỏ AG gấp đôi GD.

Cho tam giác ABC, trên cạnh AB lấy điểm P, trên cạnh AC lấy điểm Q sao cho \(PB = \frac{1}{2}PA\). \(CQ = \frac{1}{3}QA\). Nối CP với BQ cắt nhau tại I. Nối AI cắt BC tại J. Tính \(\frac{{BJ}}{{JC}} = ?\)

Cho tam giác ABC có góc A vuông, AB = 30cm, AC = 45cm. M là điểm nằm trên cạnh AB sao cho AM = 20cm.Từ M kẻ đường thẳng song song với BC cắt cạnh AC tại N. Tính diện tích AMN?

Cho hình tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho \(AB = 5AD,AC = 5AE\).

a/ So sánh \({S_{ADE}}\) và \({S_{ABC}}\)

b/ So sánh \({S_{DEHGMN}}\) và \({S_{ABC}}\). Biết rằng N trên cạnh AB, H trên cạnh AC, M và C trên cạnh BC sao cho \(AB = 5BN,AC = 5CH,BC = 5BM = 5CG\).

Cho tam giác ABC có diện tích là 180 cm², D là trung điểm của cạnh AB. Trên cạnh AC lấy E sao cho AE gấp đôi EC. Tính diện tích tam giác ADE.

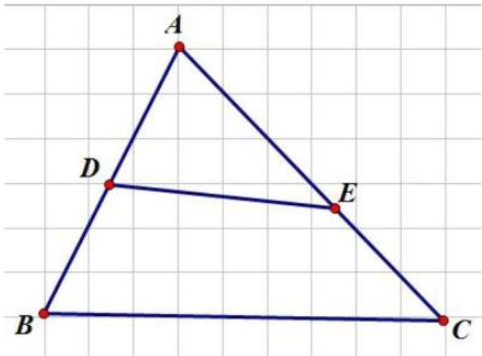
Cho tam giác ABC, có BC = 60 cm, đường cao AH = 30 cm. Trên AB lấy điểm E và D sao cho AE = ED = DB. Trên AC lấy điểm G và K sao cho AG = GK = KC. Tính diện tích hình DEGK.

Cho hình tam giác ABC, M là điểm bất kì trên cạnh BC. Nối A với M, trên AM lấy điểm N sao cho \(NM = \frac{2}{3}AM\). Nối N với B và C.

a) Viết tên các hình tam giác có trong hình vẽ.

b) So sánh diện tích tam giác NBM với diện tích tam giác ABM.

c) Tính diện tích hình tam giác ABC, biết diện tích tam giác NBC là 28 cm².

Cho tam giác ABC có các cạnh AC = 18 cm; BC = 22 cm. Biết các tam giác ABD, AEG, CDE, DEG có diện tích bằng nhau. Tính AE, DC

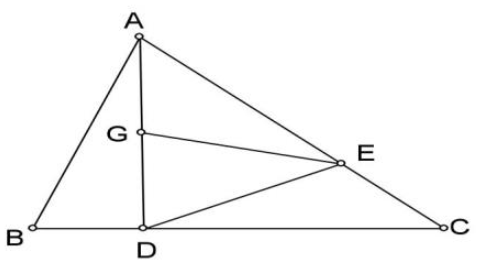
Cho tam giác ABC và các điểm D, E, F sao cho \(BD = \frac{1}{3}AB\); \(AE = CG = \frac{1}{3}AC\); \(CH = \frac{1}{3}BC\)

Tính diện tích hình BDEGH. Biết diện tích của tam giác ABC là 180 cm²

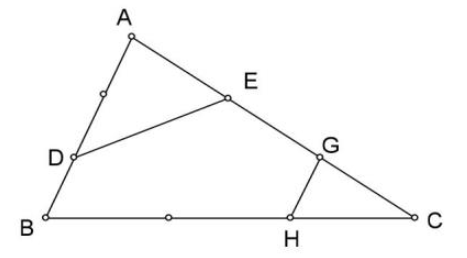
Cho hình tam giác ABC có Điểm N là điểm chính giữa cạnh AC, trên hình đó có hình thang BMNE như hình vẽ bên. Nối B với N nối E vơi M. Hai đoạn thẳng này gặp nhau ở điểm O.

a) So sánh diện tích hai hình tam giác OBM và OEN

b) So sánh diện tích hình tam giác EMC với diện tích hình AEMB

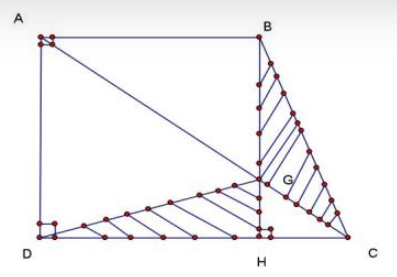
Cho hình thang vuông ABCD có góc A và D vuông. Vẽ đường cao BH. AC cắt BH tại G. Hãy so sánh diện tích tam giác DGH và diện tích tam giác GBC.

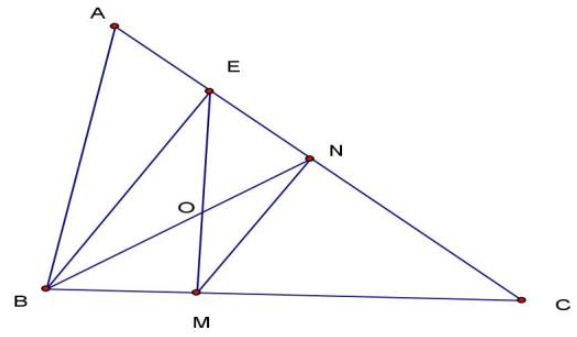
Cho hình thang ABCD có hai đáy là AB và CD. Đoạn thẳng AC cắt đoạn thẳng BD tại O:

a) So sánh diện tích hai hình tam giác DAO và BCO.

b) Biết diện tích hình tam giác BAO bằng 1 cm² và diện tích hình tam giác DCO bằng 4cm². Tính diện tích hình thang ABCD

c) Tính tỷ số hai đáy của hình thang \(\frac{{AB}}{{CD}}\)?

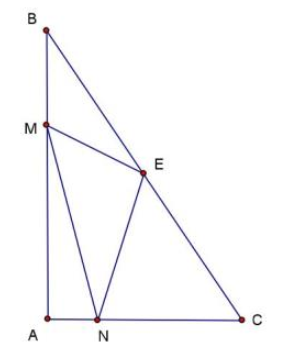
Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm M sao cho \(BM = \frac{1}{3}AB\). Trên cạnh AC lấy điểm N sao cho \(AN = \frac{1}{4}AC\). Trên cạnh BC lấy điểm E sao cho E là điểm chính giữa cạnh BC.

a) Chứng tỏ rằng \({S_{MNCB}} = \frac{5}{6}{S_{ABC}}\)

b) Chứng tỏ rằng \({S_{AMN}} = {S_{EMB}}\)

c) Biết \({S_{ABC}} = 24c{m^2}\). Tính \({S_{EMN}}\)