10 CÂU HỎI
Cho góc α = 120°. Trong các khẳng định sau, khẳng định nào là SAI?
A. \(\sin 120^\circ = \frac{{\sqrt 3 }}{2}\);
B. \(\cos 120^\circ = - \frac{1}{2}\);
C. \(\tan 120^\circ = - \sqrt 3 \);
D. \(\cot 120^\circ = \sqrt 3 \).
Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin60° = \(\frac{{\sqrt 3 }}{2}\);
B. cos60° = \(\frac{{\sqrt 3 }}{2}\);
C. tan60° = 1;
D. cot60° = −1.
Giá trị của tan135° bằng:
A. 1;
B. –1;
C. \(\frac{1}{2}\);
D. \( - \frac{1}{2}\).
Chọn phương án SAI trong các phương án dưới đây?
A. sin 0° = 0;
B. cos 90° = 0;
C. cos 0° = 1;
D. sin 90° = 0.
Cho \(\widehat A = 45^\circ \), chọn đáp án SAI trong các đáp án dưới đây?
A. sin A = \(\frac{{\sqrt 3 }}{2}\);
B. cos A = \(\frac{{\sqrt 2 }}{2}\);
C. tan A = 1;
D. cot A = 1.
Cho biết sin α = \(\frac{1}{2}\) và (180° – α) = \(\frac{a}{b}\) (với \(\frac{a}{b}\) là phân số tối giản). Tính a + b.
A. \(\frac{1}{2}\);
B. \( - \frac{1}{2}\);
C. 2;
D. 3.
Cho tam giác ABC vuông tại A có góc B bằng 60°. Tìm khẳng định đúng trong các khẳng định sau.
A. sin B = \(\frac{1}{2}\);
B. cos B = \(\frac{{\sqrt 3 }}{2}\);
C. cos C = \(\frac{{\sqrt 3 }}{2}\);
D. sin C = \(\frac{{\sqrt 3 }}{2}\).
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \]. Khi đó sin B bằng:
A. \(\frac{1}{2}\);
B. \( - \frac{1}{2}\);
C. \(\frac{{\sqrt 3 }}{2}\);
D.\( - \frac{{\sqrt 3 }}{2}\).
Giá trị của biểu thức A = cos1°.cos2°.cos3°…cos89°.cos90° là:
A. 1;
B. 0;
C. –1;
D. 2.
Cho góc α như hình vẽ, xác định giá trị của tan α.
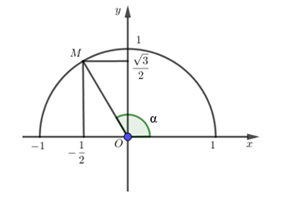
A. tan α = \( - \frac{{\sqrt 3 }}{3}\);
B. tan α = \( - \frac{{\sqrt 3 }}{2}\);
C. tan α = \( - \frac{2}{{\sqrt 3 }}\);
D. tan α = \( - \sqrt 3 \).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải