10 CÂU HỎI
Tính bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3 cm.
A. R = \(3\sqrt 2 \) cm.
B. R = \(\frac{{3\sqrt 2 }}{2}\) cm.
C. R = 3 cm.
D. R = \(\frac{{3\sqrt 3 }}{2}\) cm.
Cho tam giác ABC vuông tại A, có AB = 15 cm, AC = 20 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. R = 25.
B. R = \(\frac{{25}}{2}\).
C. R = 15.
D. R = 20.
Cho tam giác ABC vuông tại A có AB = 5 cm; AC = 12 cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. R = 26.
B. R = 13.
C. R = \(\frac{{13}}{2}\).
D. R = 6.
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 5 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.
A. R = 7,5 cm.
B. R = 13 cm.
C. R = 6 cm.
D. R = 6,5 cm.
Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.
A. R = 5 cm.
B. R = 10 cm.
C. R = 6 cm.
D. R = 2,5 cm.
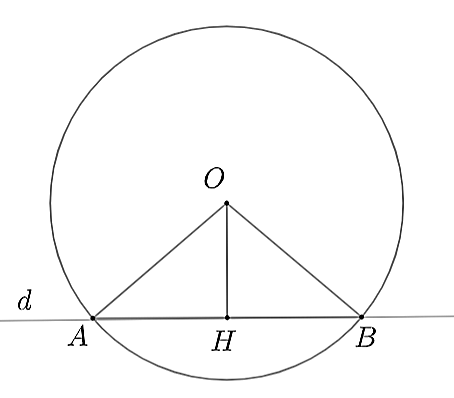
Cho đường tròn tâm O và đường thẳng d cắt đường tròn (O) tại hai điểm A và B sao cho AB = 4 cm và khoảng cách từ tâm O đến đường thẳng d là 1 cm. Tính bán kính đường tròn (O).
A. \(\sqrt 3 \)cm.
B. \(\sqrt 5 \) cm.
C. \(\frac{{\sqrt 5 }}{2}\) cm.
D. \(\frac{{\sqrt 3 }}{2}\)
Cho tam giác ABC cạnh bằng 4 cm, các đường cao là BM và CN. Gọi D là trung điểm cạnh BC. Bán kính của đường tròn đi qua bốn điểm B, N, M, C là:
A. 2 cm.
B. 4 cm.
C. 6 cm.
D. 8 cm.
Cho hình cuông ABCD cạnh 4 cm. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của CM và DN. Bán kính của đường tròn đi qua bốn điểm A, D, E, M là
A. R = 5 cm.
B. R = 10 cm.
C. R = \(2\sqrt 5 \) cm.
D. R = \(\sqrt 5 \) cm.
Cho tam giác ABC cân ở A, đường cao AH = 2 cm, BC = 8 cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D. Tính đường kính của đường tròn đi qua các điểm A, B, C, D.
A. d = 8 cm.
B. d = 12 cm.
C. d = 10 cm..
D. d = 5 cm.
Cho tam giác đều ABC. Biết rằng đường tròn (O; 4cm) đi qua ba đỉnh của tam giác. Tính diện tích tam giác ABC.
A. 24 cm2.
B. \(24\sqrt 3 \) cm2.
C. 12 cm2.
D. \(12\sqrt 3 \) cm2.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải