10 câu hỏi
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(1; +∞);
(−∞; 1);
(−1; +∞);
(−∞; −1).
Cho hàm số y = f(x)có bảng xét dấu đạo hàm như sau:
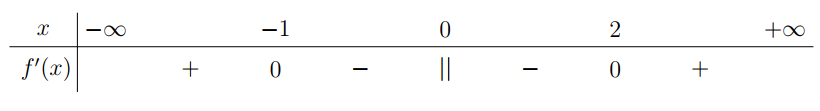
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; 0);
(2; +∞);
(0; +∞);
(−1; 2).
Hàm số nào dưới đây đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
\(y = \frac{{x - 1}}{{x - 2}}\);
y = x3 + x;
y = −x3 – 3x;
\(y = \frac{{x + 1}}{{x + 3}}\).
Cho hàm số \[y = \frac{{x - 2}}{{x + 1}}\]. Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng (−∞; +∞);
Hàm số nghịch biến trên khoảng (−1; +∞);
Hàm số nghịch biến trên khoảng (−∞; −1);
Hàm số đồng biến trên khoảng (−∞; −1).
Hàm số nào dưới đây đồng biến trên khoảng (−∞; +∞)?
y = x4 + 3x2;
\(y = \frac{{x - 2}}{{x + 1}}\);
y = 3x3 + 3x – 2;
y = 2x3 – 5x + 1.
Hàm số \(y = \frac{2}{{{x^2} + 1}}\) nghịch biến trên khoảng nào dưới đây?
(−∞; +∞);
(0; +∞);
(−∞; 0);
(−1; 1).
Cho hàm số \[y = \sqrt {2{x^2} + 1} \]. Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng (0; +∞);
Hàm số đồng biến trên khoảng (−∞; 0);
Hàm số nghịch biến trên khoảng (0; +∞);
Hàm số nghịch biến trên khoảng (−1; 1).
Cho hàm số y = f(x) liên tục trên ℝ và có đạo hàm f'(x) = (1 – x)2(x + 1)3(3 – x). Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
(−∞; 1);
(−∞; −1);
(1; 3);
(3; +∞).
Hàm số \(y = \sqrt {2018x - {x^2}} \) nghịch biến trên khoảng nào trong các khoảng sau đây?
(1010; 2018);
(2018; +∞);
(0; 1009);
(1; 2018).
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + {m^2}}}{{x + 4}}\) đồng biến trên từng khoảng xác định của nó?
5;
3;
1;
2.
