18 câu hỏi
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
0;
1;
2;
3.
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
0;
1;
2;
3.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
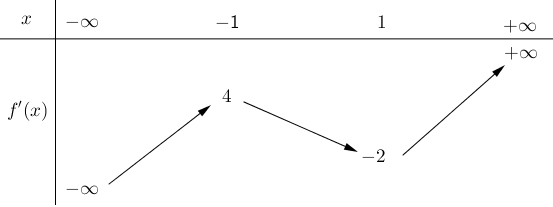
Số điểm cực trị của hàm số y = f(x2 + 2x) là
4;
5;
1;
7.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
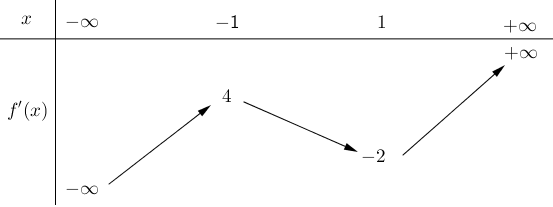
Số điểm cực trị của hàm số y = f(x2 + 2x) là
4;
5;
1;
7.
Cho hàm số y = f'(x) có đồ thị như hình vẽ
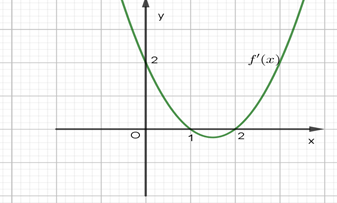
Hàm số y = f(2 – x2) đồng biến trên khoảng (a; b) khi đó a + 2b có giá trị là
1;
2;
3;
4.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1 có đồ thị như hình vẽ sau:
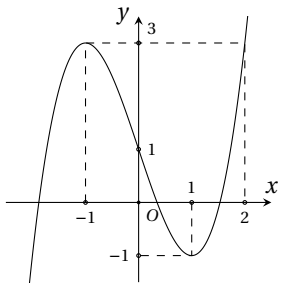
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
4;
3;
1;
2.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1 có đồ thị như hình vẽ sau:
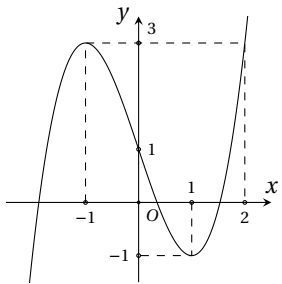
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
4;
3;
1;
2.
Cho hàm số y = f(x) có đồ thị y = f'(x) như hình sau. Hàm số g(x) = f(3 – 2x) + 2024 đồng biến trên khoảng nào dưới đây?
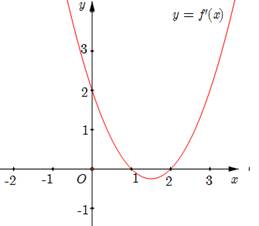
(1; +∞);
\(\left( {\frac{1}{2};1} \right)\);
\(\left( {0;\frac{1}{2}} \right)\);
\(\left( { - \infty ;\frac{1}{2}} \right)\).
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
Số điểm cực trị của hàm
số y = f(x2 – 4x + 1) là:
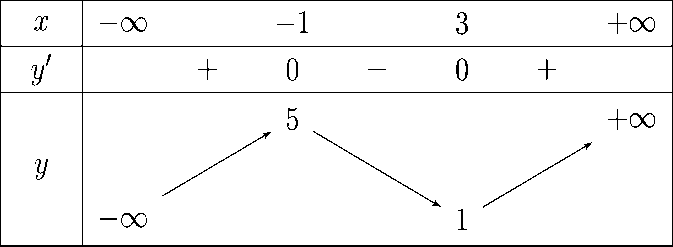
3;
2;
1;
5.
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
Số điểm cực trị của hàm
số y = f(x2 – 4x + 1) là:
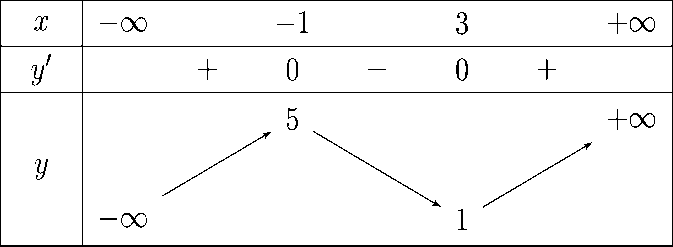
3;
2;
1;
5.
Cho hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f(2) = f(−2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ bên dưới.
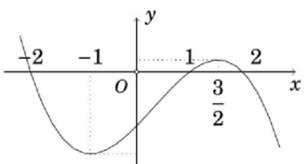
Hàm số g(x) = (f(x))2 nghịch biến trên khoảng nào dưới đây?
(−2; −1);
\(\left( { - 1;\frac{3}{2}} \right)\);
(−1; 1);
(1; 2).
Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x – 9)(x – 4)2. Khi đó hàm số g(x) = f(x2) đồng biến trên khoảng nào?
(−2; 2);
(3; +∞);
(−∞; −3);
(−∞; −3) ∪ (0; 3).
Cho hàm số y = f(x) = ax4 + bx3 + cx2 + dx + e, đồ thị hình bên là đồ thị của hàm số y = f'(x).
Xét hàm số g(x) = f(x2 – 2) . Mệnh đề nào dưới đây sai?
Hàm số g(x) nghịch biến trên khoảng (−∞; −2);
Hàm số g(x) đồng biến trên khoảng (2; +∞);
Hàm số g(x) nghịch biến trên khoảng (−1; 0);
Hàm số g(x) nghịch biến trên khoảng (0; 2).
Cho hàm số y = f'(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số g(x) = f(x2 – 2x) trên khoảng (0; +∞).
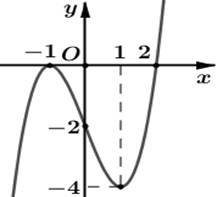
3;
2;
4;
1.
Cho hàm số y = f(x) có đạo hàm f'(x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
0;
1;
2;
3.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ, bảng biến thiên của hàm số f'(x) như sau:
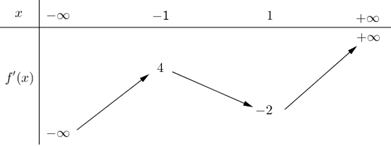
Số điểm cực trị của hàm số y = f(x2 + 2x) là
4;
5;
1;
7.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đúng hai điểm cực trị x = −1; x = 1có đồ thị như hình vẽ sau:
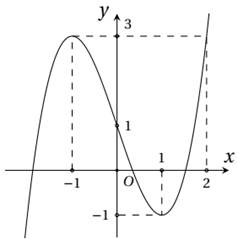
Hỏi hàm số y = f(x2 – 2x + 1) có bao nhiêu điểm cực trị?
4;
3;
1;
2.
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
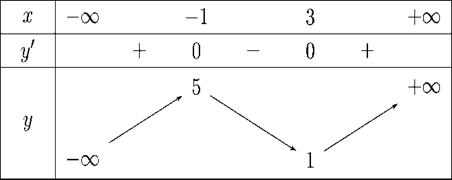
Số điểm cực trị của hàm số y = f(x2 – 4x + 1)là:
3;
2;
1;
5.
