10 CÂU HỎI
Đồ thị của hàm số y = x3 – 3x + 2 cắt trục tung tại điểm có tung độ bằng
A. 0;
B. 1;
C. 2;
D. −2.
Số giao điểm của đồ thị hàm số y = x3 – 3x + 1 và trục hoành là
A. 3;
B. 0;
C. 2;
D. 1.
Cho hàm số y = (x – 3)(x2 + 2) có đồ thị (C). Mệnh đề nào dưới đây đúng?
A. (C) cắt trục hoành tại hai điểm;
B. (C) cắt trục hoành tại một điểm;
C. (C) không cắt trục hoành;
D. (C) cắt trục hoành tại ba điểm.
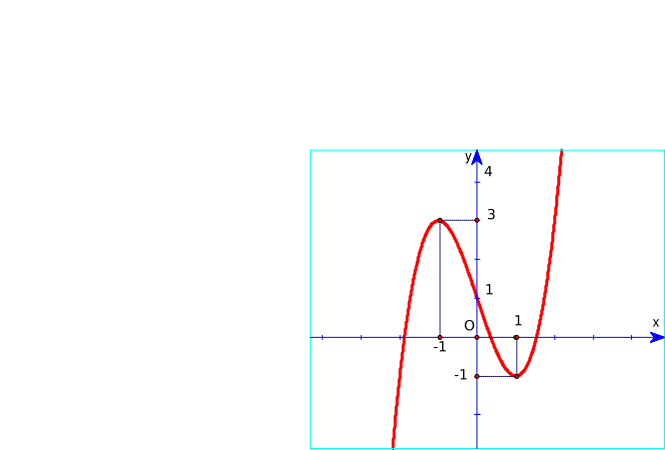
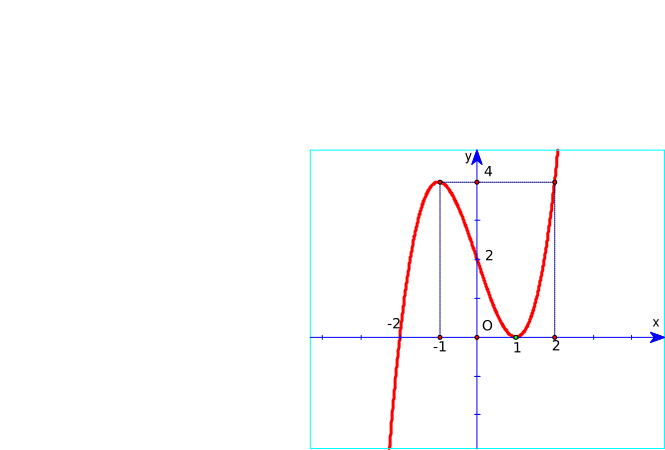
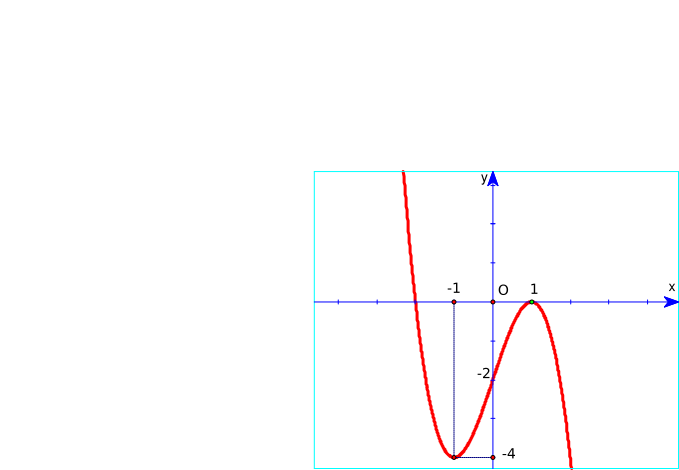
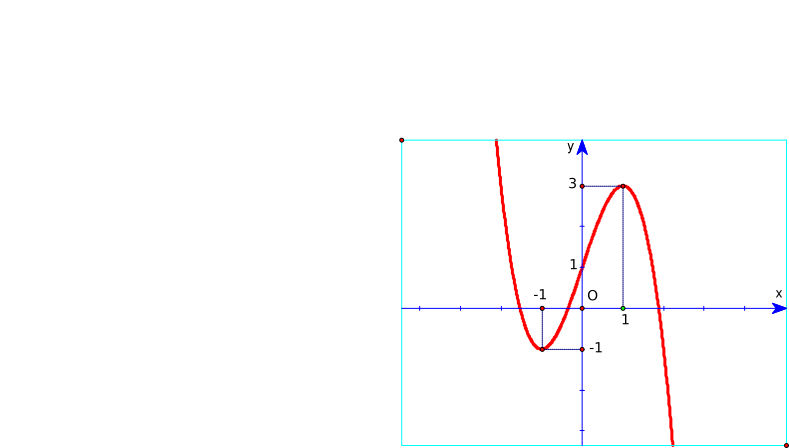
Đồ thị hàm số y = x3 – 3x + 2 là hình nào trong 4 hình dưới đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hàm số y = −x3 + 3x2 – 1 là đồ thị nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
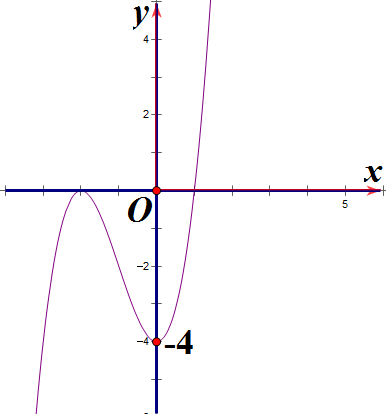
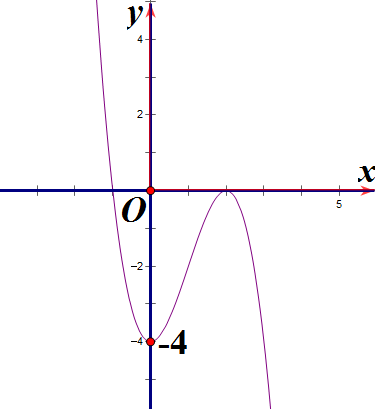
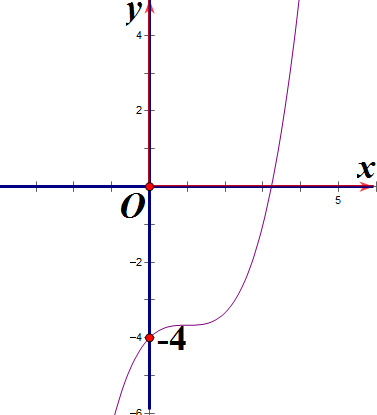
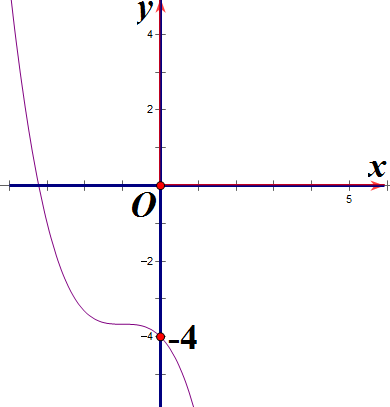
Hàm số y = x3 + 3x2 – 4 có đồ thị là hình nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
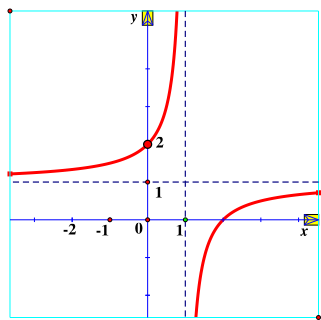
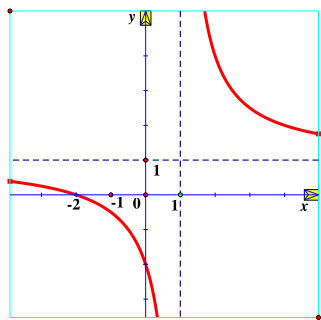
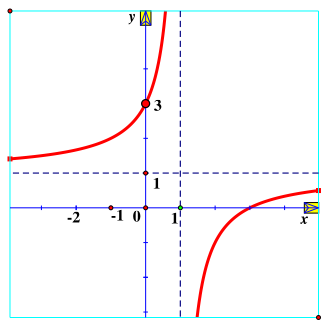
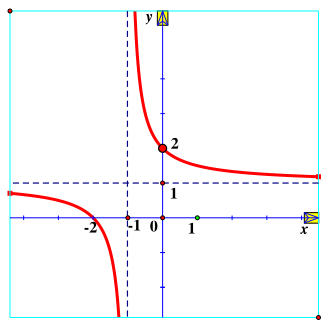
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây?
|
|
|
|
|
|
|
|
Hình 1 |
Hình 2 | Hình 3 | Hình 4 |
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x + 1}}{{x + 1}}\) có đồ thị (C). Chọn đáp án đúng.
A. Tập xác định của hàm số f(x) là D = ℝ\{−1};
B. Hàm số f(x) nghịch biến trên từng khoảng xác định của nó;
C. Đường thẳng y = x + 3 là đường tiệm cận xiên của (C);
D. Điểm I(−1; −1) là tâm đối xứng của đồ thị hàm số.
Cho hàm số \[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\]. Mệnh đề nào sau đây sai?
A. Tâm đối xứng là I(1; 3);
B. Tiệm cận đứng là đường thẳng x = 1;
C. Tiệm cận xiên là đường thẳng y = x + 3;
D. Đồ thị hàm số đi qua điểm A(2; 6).
Cho hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) có đồ thị (C). Chọn đáp án đúng.
A. Đồ thị hàm số (C) nhận đường thẳng x = 2 là tiệm cận ngang;
B. Đồ thị hàm số (C) nhận I(2; 3) là tâm đối xứng;
C. Tiếp tuyến của (C) tại giao điểm của (C) với Oy có phương trình y = −5x – 3;
D. Tích khoảng cách từ một điểm bất kỳ trên (C) tới 2 đường tiệm cận của nó luôn bằng 3.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải