10 CÂU HỎI
Cho đường tròn (O) và đường thẳng a. Kẻ OH vuông góc với đường thẳng a tại H, biết OH = R khi đó đường thẳng a và đường tròn (O)
A. Cắt nhau.
B. Tiếp xúc.
C. Không cắt nhau.
D. Không xác định được.
Nếu một đường thẳng đi qua một điểm của đường tròn và …. Thì đường thẳng ấy là một tiếp tuyến của đường tròn. Điền vào chỗ chấm.
A. song song với bán kính đi qua điểm đó.
B. đường thẳng cắt đường tròn.
C. đường thẳng không cắt đường tròn.
D. đường thẳng vuông góc với đường tròn.
Cho tam giác ABC có AC = 3 cm, AB = 4 cm, BC = 5 cm. Vẽ đường tròn (C, AC). Khẳng định nào sau đây là đúng?
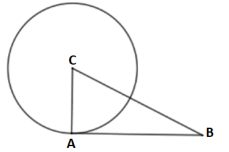
A. BC là tiếp tuyến của (C; CA).
B. AB là tiếp tuyến của (C; CA).
C. AB là cát tuyến của đường tròn (C; CA).
D. Đường thẳng BC cắt đường tròn (C; CA) tại một điểm.
Cho (O; 4 cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 4 cm), khi đó:
A. Khoảng cách từ O đến đường thẳng d bằng 4 cm.
B. Khoảng cách từ O đến đường thẳng d nhỏ hơn 4 cm.
C. Khoảng cách từ O đến đường thẳng d lớn hơn 4 cm.
D. Khoảng cách từ O đến đường thẳng d bằng 5 cm.
Cho đường tròn (O; R). Cát tuyến qua A ở ngoài (O) cắt (O) tại B và C. Cho biết AB = BC và kẻ đường kính COD. Tính độ dài đoạn thẳng AD.
A. AD = R.
B. AD = 3R.
C. AD = \(\frac{R}{2}\).
D. AD = 2R.
Cho đường tròn (O; 5 cm). Cát tuyến qua A ở ngoài (O) cắt (O) tại B và C. Cho biết AB = BC và kẻ đường kính \(\widehat {COD}\). Tính độ dài đoạn thẳng AD.
A. AD = 2,5 cm.
B. AD = 10 cm.
C. AD = 5 cm.
D. AD = 15 cm.
Cho hai đường thẳng a và b song song với nhau một khoảng là h. Một đường tròn (O) tiếp xúc với a và b. Hỏi tâm O di động trên đường nào?
A. Đường thẳng c song song và cách đều a, b một khoảng \(\frac{h}{2}\).
B. Đường thẳng c song song và cách đều a, b một khoảng \(\frac{{2h}}{3}\).
C. Đường thẳng c đi qua O vuông góc với a, b.
D. Đường thẳng (A; AB) lần lượt là tiếp điểm của a, b với (O).
Cho tam giác ABC cân tại A. Các đường tròn AH và BK cắt nhau ở I, vẽ đường tròn tâm O đường kính AI. Khi đó, ta có:
A. BK là tiếp tuyến của (O).
B. BC là tiếp tuyến của (O).
C. AC là tiếp tuyến (O).
D. HK là tiếp tuyến (O).
Cho đường tròn (O; R) đường kính AB. Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Lấy điểm M di động Ax, điểm N di động trên tia Oy sao cho AM.BN = R2. Khẳng định nào dưới đây là đúng?
A. MN là tiếp tuyến của đường tròn (O).
B. \(\widehat {MON} = 90^\circ \).
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Cho góc xOy (0° < \(\widehat {xOy}\) < 180°). Đường tròn (I) là đường tròn tiếp xúc với cả hai cạnh Ox, Oy. Khi đó điểm I chạy trên đường nào?
>
A. Đường thẳng vuông góc với Ox tại O.
B. Tia phân giác của góc xOy.
C. Tia Oz nằm giữa Ox và Oy.
D. Tia phân giác của góc xOy trừ điểm O.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải