11 bài tập Một số bài toán thực tế liên quan đến tính đơn điệu và cực trị của hàm số (có lời giải)
11 câu hỏi
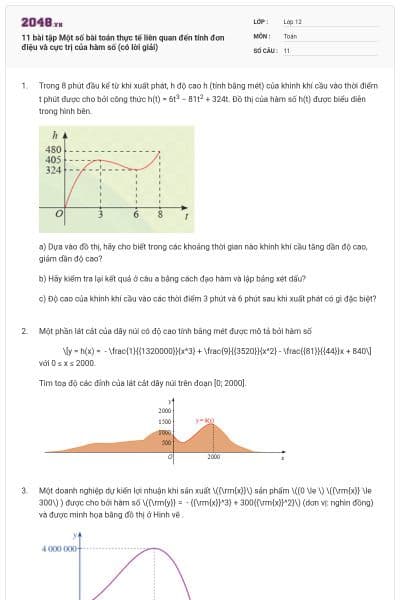
Trong 8 phút đầu kể từ khi xuất phát, h độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức h(t) = 6t3 − 81t2 + 324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên.
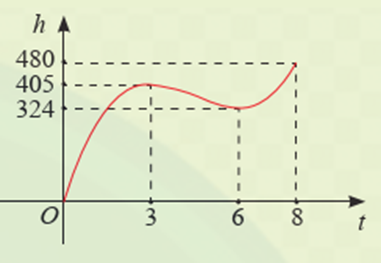
a) Dựa vào đồ thị, hãy cho biết trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao?
b) Hãy kiểm tra lại kết quả ở câu a bằng cách đạo hàm và lập bảng xét dấu?
c) Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
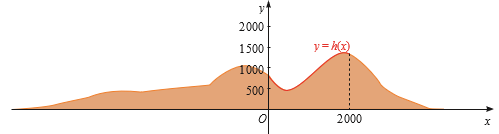
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số
\[y = h(x) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840\] với 0 ≤ x ≤ 2000.
Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000].
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất \({\rm{x}}\) sản phẩm \((0 \le \) \({\rm{x}} \le 300\) ) được cho bởi hàm số \({\rm{y}} = - {{\rm{x}}^3} + 300{{\rm{x}}^2}\) (dơn vị: nghìn đồng) và được minh họa bằng đồ thị ở Hinh vẽ .
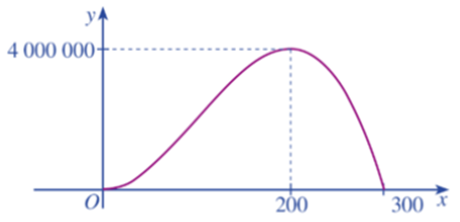
Sự thay đổi lợi nhuận theo số sản phẩm sản xuất ra và dấu của đạo hàm \({{\rm{y}}^\prime }\) có mối liên hệ với nhau như thế nào?
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức \[f(x) = 0,01{x^3} - 0,04{x^2} + 0,25x + 0,44\] (tỉ USD) với x là số năm tính từ 2010 đến 2017 \[(0 \le x \le 7)\]. (Theo: https://infographics.vn/interactive-xuat-khau-rau-qua- du-bao-bung-no-dat-4-ty-usd-trong-nam-2023/116220.vna)
a) Tính đạo hàm của hàm số y = f (x).
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số \[x\left( t \right) = {t^3} - 6{t^2} + 9t\] với t Khi đó x'(t) là vận tốc của chất điểm tại thời điểm t, kí hiệu v(t); v'(t) là gia tốc chuyển động của chất điểm tại thời điểm t, kí hiệu a(t).
a) Tìm các hàm v(t) và a(t).
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t= 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau: v(t)=0,001302t3-0,09029t2 + 23, (v được tính bằng ft/s, 1 feet = 0,3048 m) (Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012).

Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Một vật được phóng thẳng đứng lên trên từ độ cao 2 m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức \[h\left( t \right) = 2 + 24,5t{\rm{ }} - 4,9{t^2}\]. Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \[N(t) = \frac{{25t + 10}}{{t + 5}},t \ge 0\], trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và \[\mathop {\lim }\limits_{t \to + \infty } N(t)\]. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Thể tích V của 1 kg nước (tính bằng cm3) ở nhiệt độ T (đơn vị: °C) khi T thay đổi từ 0°C đến 30°C được cho xấp xỉ bởi công thức:
V = 999,87 − 0,06426T + 0,0085043T2 − 0,0000769T 3.
(Nguồn: James Stewart, J. (2015). Calculus. Cengage Learning 8th edition, p.284)
a) Tìm nhiệt độ \[{T_0} \in \] (0; 30) để kể từ nhiệt độ \[{T_0}\]trở lên thì thể tích V tăng (làm tròn kết quả đến hàng đơn vị).
b) Hỏi thể tích V giảm trong khoảng nhiệt độ nào. (làm tròn kết quả đến hàng đơn vị).
Máng trượt của một cầu trượt cho trẻ em (Hình 5a) được uốn từ một tấm kim loại có bề rộng 80 cm, mặt cắt được mô tả ở Hình vẽ. Nhà thiết kế khuyến cáo, diện tích của mặt cắt càng lớn thì càng đảm bảo an toàn cho trẻ em.
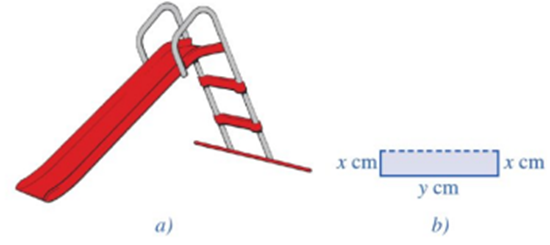
a) Gọi S là diện tích mặt cắt. Tìm điều kiện của x và viết công thức tính S theo x.
b) Với x đạt giá trị bằng bao nhiêu thì cầu trượt đảm bảo an toàn nhất cho trẻ em?
Giả sử doanh số (tính bẳng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f(t) = \frac{{5000}}{{1 + 5{e^{ - t}}}},t \ge 0\), trong đó thời gian \(t\) được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \({f^\prime }(t)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?