(Đúng sai) 18 bài tập Tính đơn diệu và cực trị của hàm số (có lời giải)

Hàm số đã cho nghịch biến trên \(\mathbb{R}\).

Hàm số đã cho không có cực trị.

Hàm số đã cho đồng biến trên từng khoảng xác định.

Hàm số đồng biến trên hai khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\), nghịch biến trên \(\left( { - 1;1} \right)\).

Hàm số đồng biến trên hai khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).

Hàm số nghịch biến trên hai khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).

Hàm số đồng biến trên \(\mathbb{R}\).

Số điểm cực trị của hàm số \[y = \frac{{5x - 1}}{{x + 2}}\] là 0.

Cho hàm số \(y = \frac{{{x^4}}}{4} - 2{x^2} + 1\). Hàm số có một cực đại và hai cực tiểu.       

Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ dưới đây.

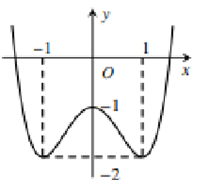
Giá trị cực đại của hàm số bằng -1.

Số cực trị của đồ thị hàm số \[y = 2{x^3} - 6x + 3\] là 2.

Hàm số đạt cực tiểu tại \(x = 2\).

Hàm số đạt cực đại tại \(x = 4\).

Hàm số có hai điểm cực trị.          

Hàm số đạt cực đại tại \(x = 0\).

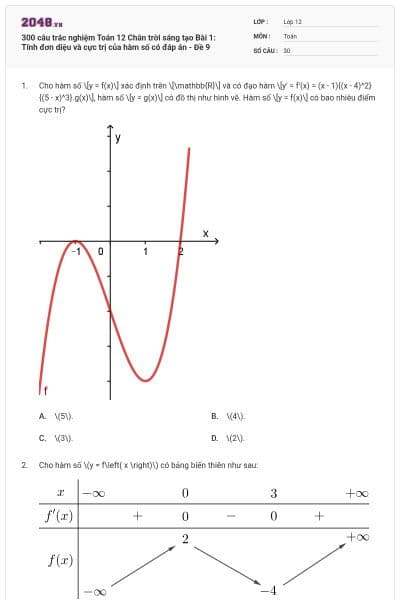
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên

Hàm số đạt cực đại tại điểm \(x = 0\)  

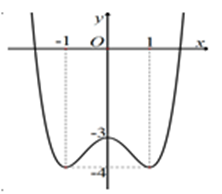
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ dưới đây. Hàm số đã cho có 2 điểm cực trị.

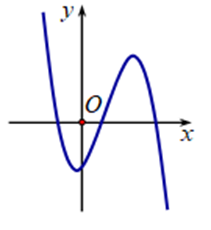
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Hàm số đạt cực tiểu tại các điểm\(x =  \pm 2\)

Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số \[y = f\left( x \right)\] bằng 3

Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và dấu của đạo hàm cho bởi bảng sau:

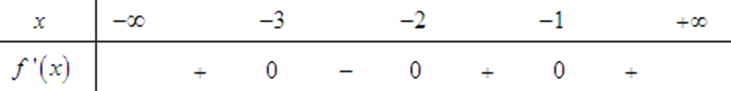
Hàm số \(f\left( x \right)\) có 3 điểm cực trị

Cho hàm số \[f(x)\] có bảng biến thiên như sau:

Điểm cực đại của hàm số là \[x = 3\]

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên.

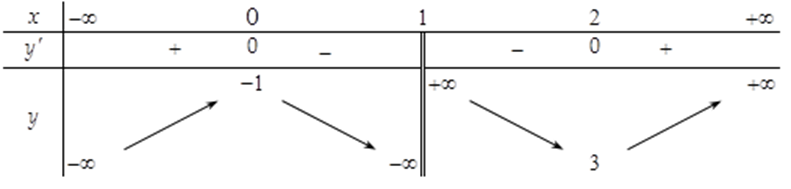
 kết luận: Hàm số có giá trị cực đại bằng \(0\).

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau

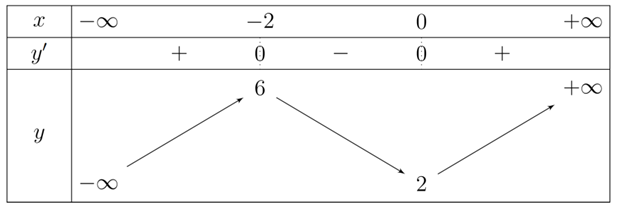
Hàm số \(y = f\left( x \right)\) đạt cực đại tại điểm\(x = 0\)

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau

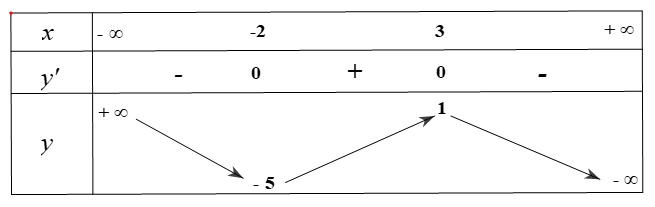
Giá trị cực đại của hàm số đã cho bằng 3

Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau

Giá trị cực đại của hàm số bằng 3

Cho hàm số \(y = f(x)\) có bảng biến thiên như sau

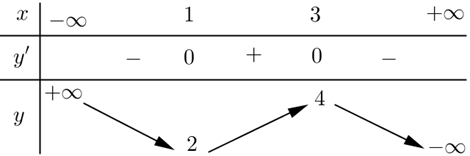
Hàm số đạt cực đại tại điểm\(x = 2.\)

Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) với bảng xét dấu đạo hàm như sau

Hàm số \(y = f(x)\) có 2 điểm cực.

hàm số nghịch biến trên \(\left( {1;\,\,3} \right).\)

hàm số đồng biến trên \(\left( { - \infty ;\,\,0} \right).\)

hàm số đồng biến trên khoảng \(\left( {\frac{1}{2};\,\,\frac{3}{2}} \right).\) 

hàm số đồng biến trên  \(\left( {0;\,\,3} \right).\)

Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).

Hàm số đồng biến trên khoảng \(\left( { - 1;3} \right)\).

Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right).\)

Hàm số đồng biến trên   \[\left( {0;\, + \infty } \right)\].

Hàm số đồng biến trên \[\left( { - \infty ;\,0} \right)\].

Hàm số đồng biến trên \[\left( { - \infty ;\, - 1} \right)\]

Hàm số nghịch biến trên  \[\left( { - 1;\,1} \right)\].

\(y' > 0,\,\forall x \in \mathbb{R}.\)      

\(y' > 0,\,\forall x \ne 1.\)

\(y' < 0,\,\forall x \in \mathbb{R}.\)

\(y' < 0,\,\forall x \ne 1.\)

Điểm cực đại của đồ thị hàm số \(y = {x^3} - 12x + 12\) là \(\left( {4\,;\,28} \right)\)

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình bên.

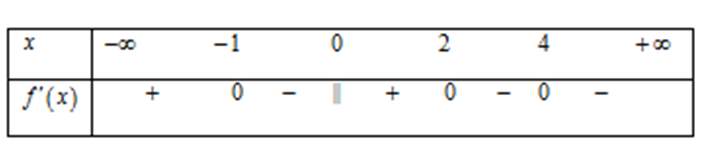
Số điểm cực trị của hàm số đã cho là 3

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có \(f'\left( x \right) = \left( {2x - 3} \right){\left( {x + 1} \right)^2}{\left( {x - 2} \right)^3}\left( {4 - x} \right)\). Số điểm cực đại của hàm số \(y = f\left( x \right)\) là 2

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right)\left( {{x^2} - 2} \right)\left( {{x^4} - 4} \right)\). Số điểm cực trị của hàm số \(y = f\left( x \right)\) là 1

$y=-x^3+2x^2-2024x$ không nghịch biến trên $\mathrm{ℝ}$.

\(y =  - 5x + \sin x\) không nghịch biến trên $\mathrm{ℝ}$.

 $y=\frac{2024}{x^2+1}$không nghịch biến trên $\mathrm{ℝ}$

\(y = {\left( {\frac{\pi }{{\sqrt 3  + \sqrt 5 }}} \right)^x}\)không nghịch biến trên R.

Hàm số \(y = f\left( {x - 2} \right)\)nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\).

Hàm số \(y = f\left( {x - 2} \right)\)nghịch biến trên khoảng \(\left( {2; + \infty } \right)\).

Hàm số \(y = f\left( {x - 2} \right)\)đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).

Hàm số \(y = f\left( {x - 2} \right)\)nghịch biến trên khoảng \(\left( {2;4} \right)\).

Hàm số \[g(x) = {[f(x)]^2}\]nghịch biến trên  \[( - \infty ;3)\].   

Hàm số \[g(x) = {[f(x)]^2}\]nghịch biến trên \[(1;3)\].

Hàm số \[g(x) = {[f(x)]^2}\]nghịch biến trên  \[(3; + \infty )\].                         

Hàm số \[g(x) = {[f(x)]^2}\]nghịch biến trên  \[( - 3;1)\].

Hàm số \(y = f\left( {2x - 3{x^2}} \right)\) đồng biến trên khoảng   \[\left( {\frac{1}{3}\,;\,\frac{1}{2}} \right)\].

Hàm số \(y = f\left( {2x - 3{x^2}} \right)\) đồng biến trên khoảng  \[\left( {\frac{1}{2}\,;\, + \infty } \right)\].     

Hàm số \(y = f\left( {2x - 3{x^2}} \right)\) đồng biến trên khoảng \[\left( { - \infty \,;\,\frac{1}{3}} \right)\].

Hàm số \(y = f\left( {2x - 3{x^2}} \right)\) đồng biến trên khoảng   \[\left( { - 2\,;\,\frac{1}{2}} \right)\].

Cực đại của hàm số \(y = x\sqrt {1 - {x^2}} \) là \(\frac{1}{2}\)

Điểm thuộc đường thẳng \(d:\)\(x - y - 1 = 0\) cách đều hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) là \(I\left( {1; - 1} \right)\)

Biết \[M\left( {-{\rm{ }}2;21} \right)\] là điểm cực đại của đồ thị hàm số \(y = 2{x^3} + b{x^2} + cx + 1\). Điểm cực tiểu của đồ thị hàm số đã cho là \(\left( {1; - 6} \right)\)

Gọi\(A,\,B,\,C\) là ba điểm cực trị của đồ thị hàm số \(y = {x^4} - 2{x^2} + 2\). Diện tích của tam giác \(ABC\) bằng 2.

Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ.

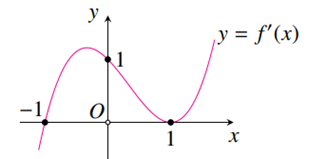
Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại điểm \(x =  - 1\)

Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ dưới đây

Số điểm cực trị của hàm số \[g\left( x \right) = f\left( {{x^2} - 3x} \right)\] là 6

Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Đồ thị của \(y = f'\left( x \right)\) như hình dưới đây

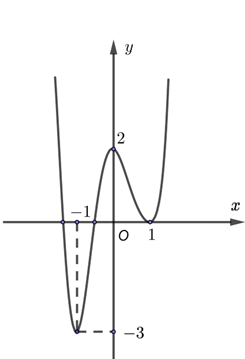
Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {4{x^2} - 4x} \right)\) là 3

Cho hàm số \(f\left( x \right)\), bảng biến thiên của hàm số \(f'\left( x \right)\) như sau

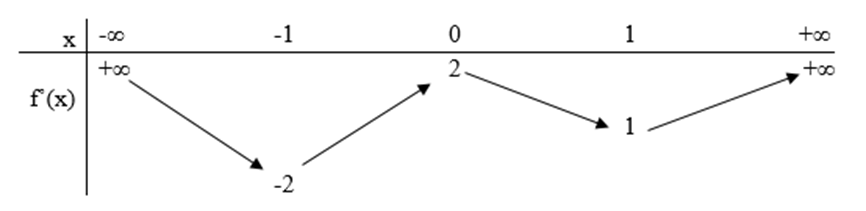
Số điểm cực trị của hàm số \(y = f\left( {{x^2} + 2x} \right)\) là 5