20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1: Tính đơn diệu và cực trị của hàm số (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Hàm số nào dưới đây luôn nghịch biến trên ℝ?
A. ![]() .
.
B. ![]() .
.
y = 3 – 2x – x3.
D. ![]() .
.
Cho hàm số y = f(x) có đồ thị như hình dưới đây
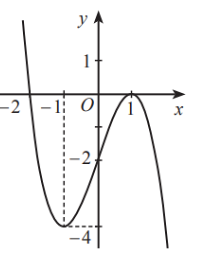
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng sau đây?
(−∞; −1).
(−1; 1).
(−2; 1).
(1; +∞).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau:
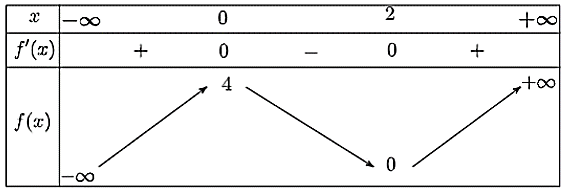
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−∞; 0).
(−∞; 2).
(0; 2).
(0; +∞).
Cho hàm số ![]() . Tìm mệnh đề đúng.
. Tìm mệnh đề đúng.
Hàm số nghịch biến trên các khoảng (−∞; −1) và (−1; +∞).
Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
Hàm số nghịch biến trên tập (−∞; 1) ∪ (1; +∞).
Hàm số nghịch biến trên tập ℝ\{−1}.
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị hàm số y = f'(x) là đường cong trong hình vẽ. Hàm số y = f(x) đã cho đồng biến trên khoảng nào dưới đây?
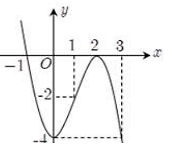
(2; +∞).
(−4; 0).
(0; 2).
(−∞; −1).
Tìm điểm cực tiểu của đồ thị hàm số ![]() .
.
x = 1.
B. ![]() .
.
x = 3.
(3; 1).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu đạo hàm như sau

Hàm số đã cho có bao nhiêu điểm cực trị?
3.
1.
4.
2.
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau:
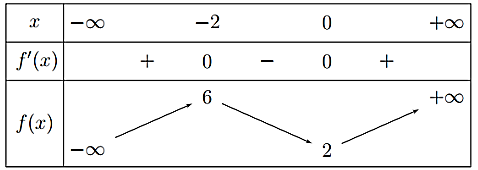
Giá trị cực tiểu của hàm số đã cho là
−2.
0.
2.
6.
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình dưới đây
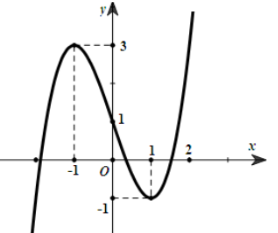
Phát biểu nào sau đây là đúng
xCT = −1, xCĐ = 1.
xCT = −1, xCĐ = 3.
xCT = 3, xCĐ = −1.
xCT = 1, xCĐ = −1.
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x2 – 1)(x – 2)2. Số điểm cực tiểu của đồ thị hàm số đã cho là
4.
1.
3.
2.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
a) Hàm số f(x) nghịch biến trên khoảng (−∞; −2).
b) Hàm số f(x) có ba điểm cực trị
c) Điểm cực đại của đồ thị hàm số là x = 0
d)Hàm số y = f(x + 3) đồng biến trên khoảng (−1; +∞).
a) Hàm số f(x) có 3 điểm cực trị
b) Hàm số f(x) đồng biến trên khoảng (−∞; −1).
c) Hàm số f(x) đạt cực đại tại x = 0.
d) f(0) < f(1)
a) Phương trình f'(x) = 0 có hai nghiệm là x = 2 và x = −2
b) Hàm số y = f(x) đạt cực đại tại x = 2
c) Hàm số y = f(x) có giá trị cực tiểu bằng f(2).
d) Hàm số y = f(x2) có 3 điểm cực trị.
a) Tập xác định của hàm số là (1; +∞).
b) Hàm số có đạo hàm là y' = 3x2 + 6x + 9
c) Hàm số đồng biến trên khoảng (−3; 1)
d) Đồ thị hàm số đạt cực trị tại 2 điểm A, B. Chu vi của tam giác OAB bằng ![]() (với O là gốc tọa độ).
(với O là gốc tọa độ).
a) Hàm số đồng biến trên khoảng (7; +∞)
b) f(1) < f(3)
c) Hàm số nghịch biến trên khoảng (1; 7).
d) Phương trình f'(3x – 1) = 0 nhận ![]() làm nghiệm.
làm nghiệm.
PHẦN II. TRẢ LỜI NGẮN
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 4)(x2 – 2x), ∀x Î ℝ. Biết hàm số y = f(x) nghịch biến trên khoảng (a; b). Tính b – a.
Biết đồ thị hàm số y = x3 – 3x2 + 2ax + b (a; b Î ℝ) có điểm cực tiểu A(2; −2). Tính a + b.
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng phóng đi tại thời điểm t = 126 (s) cho bởi hàm số sau đây:
v(t) = 0,001302t3 – 0,09029t2 + 23 (v được tính bằng ft/s, 1 feet = 0,3048 m).

Gọi (a; b) là khoảng thời gian gia tốc của tàu con thoi sẽ tăng tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi.Tính T = a + b.
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy được mô phỏng ở hình bên dưới. Đường bay của nó có dạng là một phần của đồ thị hàm số bậc ba
y = ax3 + bx2 + cx + d (a ≠ 0) với x Î [−4; 0], vị trí bắt đầu hạ cánh có tọa độ (−4; 1) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số.
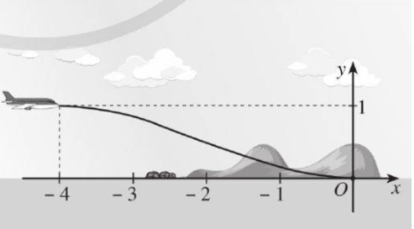
Tính ![]() .
.
Cho hàm số y = f(x) có đạo hàm trên ℝ và đồ thị hàm số y = f'(x) như hình vẽ dưới đây
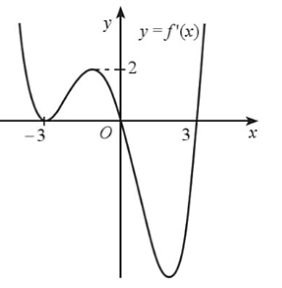
Xét hàm số g(x) = f(x) – x. Hàm số g(x) có bao nhiêu điểm cực trị?