109 CÂU HỎI
Cho đường tròn (C) đường kính AB và đường thẳng . Để hình tròn xoay sinh bởi (C) khi quay quanh là một mặt cầu thì cần có thêm điều kiện nào sau đây:
(I) Đường kính AB thuộc .
(II) cố định và đường kính AB thuộc .
(III) cố định và hai điểm A, B cố định trên .
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III).
D. Không cần thêm điều kiện nào.
Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt (P) tại N. Hình chiếu của O trên (P) là I. Mệnh đề nào sau đây đúng?
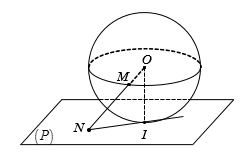
A. NI tiếp xúc với (S)
B.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
A.
B.
C.
D.
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho . Khi đó khoảng cách từ O đến BC bằng:
A.
B.
C.
D.
Cho mặt cầu S(O;R) và mặt phẳng . Biết khoảng cách từ O đến bằng . Khi đó thiết diện tạo bởi mặt phẳng với S(O;R) là một đường tròn có đường kính bằng:
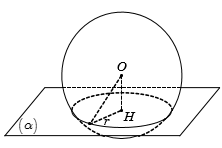
A.
B.
C.
D.
Cho mặt cầu tâm I bán kính R = 2,6 cm. Một mặt phẳng cắt mặt cầu và cách tâm I một khoảng bằng 2,4 cm. Thế thì bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:
A. 1,2 cm
B. 1,3 cm
C. 1 cm
D. 1,4 cm
Diện tích hình tròn lớn của một hình cầu là p . Một mặt phẳng cắt hình cầu theo một hình tròn có diện tích là . Khoảng cách từ tâm mặt cầu đến mặt phẳng bằng:
A.
B.
C.
D.
Một hình cầu có bán kính là 2m, một mặt phẳng cắt hình cầu theo một hình tròn có độ dài là . Khoảng cách từ tâm mặt cầu đến mặt phẳng là:
A. 1,6m
B. 1,5m
C. 1,4m
D. 1,7m
Cho mặt cầu S(O;R), A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60o . Diện tích của đường tròn giao tuyến bằng:
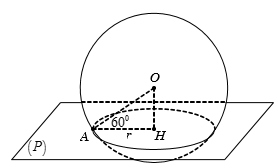
A.
B.
C.
D.
Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy bằng a. Khi đó mặt cầu nội tiếp hình chóp S.ABCD có bán kính bằng:
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD ta được:
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
A.
B.
C.
D.
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng . Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số bằng:
A.
B.
C.
D.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60o . Thể tích của khối cầu ngoại tiếp khối chóp S.ABCD là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AD = 2a, AB = BC = CD = a. Cạnh bên SA = 2a và vuông góc với đáy. Gọi R là bán kính mặt cầu ngoại tiếp khối chóp S.ABCD. Tỉ số nhận giá trị nào sau đây?
A.
B. a
C. 1
D.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a. Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng 45o. Gọi N là trung điểm SA, h là chiều cao của khối chóp S.ABCD và R là bán kính mặt cầu ngoại tiếp khối chóp N.ABC. Biểu thức liên hệ giữa R và h là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Đường thẳng vuông góc với đáy (ABCD). Gọi M là trung điểm SC, mặt phẳng đi qua hai điểm A và M đồng thời song song với BD cắt SB, SD lần lượt tại E, F. Bán kính mặt cầu đi qua năm điểm S, A, E, M, F nhận giá trị nào sau đây?
A.
B. a
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc đáy (ABCD). Gọi H là hình chiếu của A trên đường thẳng SB. Bán kính mặt cầu ngoại tiếp tứ diện HBCD có giá trị nào sau đây?
A.
B. a
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKCB là:
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
A.
B.
C.
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60o . Gọi G là trọng tâm tam giác SAC , R là bán kính mặt cầu có tâm G và tiếp xúc với mặt phẳng (SAB) . Đẳng thức nào sau đây sai?
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
A.
B.
C.
D.
Cho tứ diện O.ABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, OB = 2a, OC = 3a. Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là:
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc 60o . Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số bằng ?
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Cạnh bên và vuông góc với đáy (ABCD). Bán kính mặt cầu ngoại tiếp khối chóp S.ACD nhận giá trị:
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C và BC = a. Mặt phẳng (SAB) vuông góc với đáy, SA = SB = a, . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.
B.
C. a
D. 2a
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, , . Góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60o . Bán kính mặt cầu ngoại tiếp tứ diện A'.ABC bằng:
A.
B.
C.
D.
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60o và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A'B'C' bằng:
A.
B.
C.
D.
Người ta định nghĩa mặt cầu (S) như sau, hãy chọn câu trả lời đúng.
A. { và }
B. { và }
C. Mặt cầu (S) là mặt sinh ra bởi một đường tròn khi quay quanh một đường kính.
D. Ba câu A, B và C
Phương trình mặt câu tâm I(a, b,c ) có bán kính R là:
A.
B.
C.
D.
là phương trình của mặt cầu khi và chỉ khi:
A.
B. d < 0
C. d > 0
D.
Điều kiện để là một mặt cầu là:
A.
B.
C.
D.
Cho hai mặt cầu (S) và (S’) lần lượt có tâm I và J, bán kính R và R’. Đặt d = IJ. Câu nào sau đây sai?
I. và (S') trong nhau
II. và (S') ngoài nhau
III. và (S') tiếp xúc ngoài
IV. và (S') tiếp xúc trong
A. Chỉ I và II
B. Chỉ I và III
C. Chỉ I và IV
D. Tất cả đều sai.
Hai mặt cầu và , cắt nhau theo đường tròn có phương trình :
A.
B.
C.
D. Hai câu A và B
Cho mặt cầu và mặt phẳng
I. cắt (S)
II. tiếp xúc (S)
III. không cắt (S)
A. Chỉ I và II
B. Chỉ I và III
D. Chỉ II
D. Chỉ II
Trong không gian với hệ trục tọa độ Oxyz cho 2 điểm A(1;3;0), B(-2;1;1) và đường thẳng: . Viết phương trình mặt cầu đi qua A, B và có tâm I thuộc
A.
B.
C.
D.
Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu?
A.
B.
C.
D.
Giá trị phải thỏa mãn điều kiện nào để mặt cong là mặt cầu: ?
A.
B.
C.
D.
Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu:
A.
B.
C.
D.
Tìm tập hợp các tâm I của mặt cầu
A. Đường thẳng:
B. Phần đường thẳng: với
C. Phần đường thẳng: với
D. Phần đường thẳng: với
Với giá trị nào của m thì mặt phẳng tiếp xúc với mặt cầu
A.
B.
C.
D.
Với giá trị nào của m thì mặt phẳng cắt mặt cầu ?
A.
B.
C.
D.
E.
Mặt phẳng và mặt cầu
A. Tiếp xúc
B. Không cắt nhau
C. Cắt nhau
D. (P) qua tâm của (S)
Xét vị trí tương đối của mặt cầu và mặt phẳng
A. Cắt nhau
B. Tiếp xúc
C (Q) là mặt phẳng đối xứng của (S)
D. Không cắt nhau
Hai mặt cầu ;
A. Tiếp xúc ngoài
B. Cắt nhau
C. Tiếp xúc ngoài
D. Cắt nhau.
Hai mặt cầu
A. Ngoài nhau
B. Cắt nhau
C. Tiếp xúc trong
D. Trong nhau
Cho mặt cầu và mặt phẳng . Gọi (C) là đường tròn giao tuyến của (P) và (S). Tính tọa độ tâm H của (C).
A.
B.
C.
D.
Cho mặt cầu và mặt phẳng . Gọi (C) là đường tròn giao tuyến của (P) và (S). Viết phương trình mặt cầu cầu (S') chứa (C) và điểm M(1,-2,1)
A.
B.
C.
D.
Cho hai mặt cầu và Gọi (C) là giao tuyến của (S) và (S'). Viết phương trình của (C)
A.
B.
C.
D. Hai câu A và C
Cho hai mặt cầu và Gọi (C) là giao tuyến của (S) và (S'). Viết phượng trình mặt cầu qua (C) và điểm A(2,1,-3)
A.
B.
C.
D.
Cho mặt cầu . Viết phương trình tổng quát của đường kính AB song song với đường thẳng
A.
B.
C.
D.
Cho mặt cầu . Viết phương trình giao tuyến của (S) và mặt phẳng (yOz).
A.
B.
C.
D.
Cho mặt cầu . Viết phương trình tổng quát của mặt phẳng đối xứng (P) của (S) vuông góc với đường kính qua gốc O
A.
B.
C.
D.
Cho mặt cầu . Gọi A là giao điểm của (S) và trục y'Oy có tung độ âm. Viết phương trình tổng quát của tiếp diện (Q) của (S) tại A
A.
B.
C.
D.
Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD với A(0,-1,0); B(2,0,1); C(1,0,-1); D(1,-1,0)
A.
B.
C.
D.
Với giá trị nào của m thì mặt cầu tiếp xúc trục z'Oz
A. -2
B. 2
C.
D.
Với giá trị nào của m thì hai mặt cầu sau tiếp xúc trong?
A.
B. m = 12
C. m = 6
D. m = 18
Tính bán kính của đường tròn giao tuyến của mặt phẳng và mặt cầu
A.
B. 1
C. 7
D.
Viết phương trình mặt cầu (S) tâm I(-2,1,-1) qua A(4,3,-2)
A.
B.
C.
D.
Viết phương trình mặt cầu (S) tâm E(-1,2,4) qua gốc O
A.
B.
C.
D.
Viết phương trình mặt cầu (S) đường kính AB với A(4,-3,5); B(2,1,3)
A.
B.
C.
D.
Viết phương trình mặt cầu (S) tiếp xúc với hai mặt phẳng song song và có tâm I ở trên trục y'Oy
A.
B.
C.
D.
Viết phương trình mặt cầu (S) tâm I(1,2,-3) tiếp xúc với mặt phẳng
A.
B.
C.
D.
Viết phương trình tổng quát của tiếp diện của mặt cầu song song với mặt phẳng
A.
B.
C.
D.
Viết phươngng trình mặt cầu (S) tâm I(4,2,-1) nhận đường thẳng (D): làm tiếp tuyến.
A.
B.
C.
D.
Viết phương trình tiếp diện của mặt cầu qua trục y’Oy.
A.
B.
C.
D.
Viết phương trình mặt cầu (S) tâm I(-3,2,2) tiếp xúc với mặt cầu (S’):
A.
B.
C.
D.
Viết phương trình mặt cầu (S) qua gốc O và các giao điểm của mặt phẳng với ba trục tọa độ
A.
B.
C.
D.
Cho mặt cầu và mặt phẳng . Gọi M là tiếp điểm của (S) và tiếp diện di động (Q) vuông góc với (P). tập hợp các điểm M là:
A. Mặt phẳng:
B. Mặt phẳng:
C. Đường tròn:
D. Đường tròn:
Cho mặt cầu và mặt phẳng . Viết phương trình mặt cầu (S’) có bán kính nhỏ nhất chứa giao tuyến của (S) và (P).
A.
B.
C.
D.
Cho tứ diện ABCD có A(1,1,1); B(3,3,1); C(3,1,3); D(1,3,3). Viết phương trình mặt cầu ( S1 ) tiếp xúc với 6 cạnh của tứ diện
A.
B.
C.
D.
Cho tứ diện ABCD có A(1,1,1); B(3,3,1; C(3,1,3); D(3,1,3). Viết phương trình mặt cầu ( S2 ) nội tiếp tứ diện.
A.
B.
C.
D.
Viết phương trình mặt cầu ( S3 ) ngoại tiếp tứ diện.
A.
B.
C.
D.
Viết phương trình mặt cầu (S) qua ba điểm A(2,0,1); B(1,3,2); C(3,2,0) có tâm nằm trong mặt phẳng (xOy)
A.
B.
C.
D.
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Viết phương trình mặt cầu ( S1 ) ngoại tiếp hình lập phương.
A.
B.
C.
D.
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Viết phương trình mặt cầu ( S2 ) nội tiếp hình lập phương.
A.
B.
C.
D.
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Viết phương trình mặt cầu ( S3 ) tiếp xúc với tất cả các cạnh của hình lập phương.
A.
B.
C.
D.
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Sáu mặt phẳng chia hình lập phương thành bao nhiêu phân bằng nhau?
A. 10
B. 8
C. 4
D. 6
Cho hai điểm A(2,-3,-2); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) sao cho
A. Mặt cầu
B. Mặt cầu
C. Mặt cầu
D. Mặt cầu
Cho hai điểm A(2,-3,-1); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
A. Mặt cầu
B. Mặt phẳng
C. Mặt cầu
D. Mặt cầu
Cho hai điểm A(2,-3,-1); B()-4,5,-3. Tìm tập hợp các điểm M(x, y, z) thỏa mãn
A. Mặt phẳng
B. Mặt cầu
C. Mặt cầu
D. Mặt cầu
Cho hai điểm A(2,-3,-1); B(-4,5,-3). Định k để tập hợp các điểm M(x, y, z) sao cho , là một mặt cầu.
A.
B.
C.
D.
Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
A. Mặt cầu
B. Mặt cầu
C. Mặt cầu
D. Mặt phẳng
Cho tứ diện OABC với A(-4,0,0); B(0,6,0); C(0,0,-8). Mặt cầu (S) ngoại tiếp từ diện có tâm và bán kính là:
A.
B.
C.
D.
Tìm tập hợp các tâm I của mặt cầu ;
A. Phần đường thẳng
B. Phần đường thẳng
C. Mặt phẳng
D. Mặt phẳng
Tìm tập hợp các tâm I của mặt cầu
A. Đường thẳng
B. Mặt phẳng
C. Đường tròn với và
D. Đường tròn
Tìm tập hợp các tâm I của mặt cầu (S): ,
A. Mặt phẳng:
B. Mặt phẳng
C. Phần đường thẳng: với
D. Elip:
Tìm tập hợp các tâm I của mặt cầu (S) có bán kinh thay đổi tiếp xúc với hai mặt phẳng
A. Mặt phẳng:
B. Hai mặt phẳng: ;
C. Hai phẳng:
D. Mặt phẳng:
Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng
A. Mặt phẳng:
B. Mặt phẳng:
C. Mặt phẳng:
D. Mặt phẳng:
Tìm tập hợp các tâm I của mặt cầu (S) có bán kính R = 3 tiếp xúc với mặt phẳng
A. Hai mặt phẳng:
B. Hai mặt phẳng:
C. Hai mặt phẳng:
D. hai mặt phẳng:
Tìm tập hợp các điểm M có cùng phương tích với hai mặt cầu ;
A. Mặt phẳng:
B. Mặt phẳng:
C. Mặt phẳng:
D. Mặt phẳng:
Cho mặt (S) tâm I ở trên z’Oz tiếp xúc với hai mặt phẳng và . Tính tọa độ tâm I và bán kính R:
A.
B.
C.
D. Hai câu A và C
Cho hình hợp chữ nhật ABCD.EFGH có A(0,0,0); B(4,0,0); D(0;6;0); E(0,0,2). Tính diện tích mặt cầu (S) ngoại tiếp hình hợp chữ nhật.
A. đvdt
B. 42 đvdt
C. đvdt
D. đvdt
E. Đáp số khác
Cho hình hợp chữ nhật ABCD.EFGH có A(0,0,0); B(4,0,0); D(0,6,0); E(0,0,2). Ba mặt phẳng: x - 2z = 0; y - 3 = 0; x + 2z - 4 = 0 chia hình hộp chữ nhật thanh mấy phần bằng nhau?
A. 10
B. 8
C. 6
D. 4
Cho tứ diện ABCD có A(1,2,3); B(0,0,3); C(0,2,0); D(1,0,0). Tìm tập hợp các điểm M thỏa mãn
A. Mặt cầu:
B. Mặt cầu:
C. Mặt phẳng:
D. Mặt phẳng:
Cho mặt cầu (S): và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tìm tập hợp các điểm M.
A. Đường tròn:
B. Đường tròn:
C. Đường tròn:
D. Hai câu A và B
Cho mặt cầu (S): và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Gọi (P) là tiếp điểm của (S) tại M và là mặt phẳng qua M cắt hình cầu (S) theo hình trơn có diện tích bằng diện tích hình trơn lớn của (S). Tính góc tạo bởi (P) và (Q)
A.
B.
C.
D.
Cho mặt cầu (S): và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tính tọa độ giao điểm của AI và mặt cầu (S).
A.
B.
C.
D.
Cho tứ diện ABCD có A(3, 6, -2); B(6, 0, 1); C(-1, 2, 0); D(0, 4, 1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ :
A. I(3, -2, 1)
B. (3, 2, -1)
C. I(-3, 2, 1)
D. I(3, -2, -1)
Trong không gian Oxyz cho mặt cầu (S) có phương trình , (S) có tọa độ tâm I và bán kính R là
A.
B.
C.
D.
Trong không gian Oxyz cho đường tròn: . Tọa độ tâm H của (C) là:
A.
B.
C.
D.
Trong không gian cho đường tròn . Bán kính r của đường tròn (C) bằng :
A.
B.
C.
D.
Trong không gian Oxyz cho đường tròn . Bán kính r của (C) bằng:
A.
B.
C.
D.
Trong không gian tọa độ Oxyz cho đường tròn . Tâm H của (C) là điểm có tọa độ:
A.
B.
C.
D.
Trong không gian Oxyz cho đường tròn . Bán kính r của đường tròn (C) bằng :
A.
B.
C.
D.
Trong không gian Oxyz cho đường tròn (C) có tâm H và bán kính r bằng:
A.
B.
C.
D.
Cho mặt cầu và ba điểm A(1,2,-2); B(-4,2,3); C(1,-3,3) nằm trên mặt cầu (S). Bán kính r của đường tròn ngoại tiếp tam giác ABC là :
A.
B.
C.
D.

