10 CÂU HỎI
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là
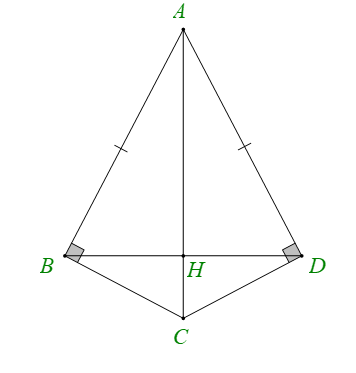
A. ;
B. ;
C. AC ⊥ BD;
D. H là trung điểm của BD.
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết . Số đo góc ACB là
A. 150°;
B. 60°;
C. 30°;
D. 90°.
Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là
A. AE;
B. DC;
C. ED;
D. ED và DC.
Cho khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?
A. ∆OBM = ∆OMA;
B. ;
C.∆OBM = ∆OBA;
D. OM là tia phân giác của góc .
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
A. BD = CE;
B. BE = CD;.
C. BK = KC;
D. DK = KC
Cho ∆ABC cân tại A. Trên 2 cạnh AB và AC lấy hai điểm M và N sao cho AM = AN. So sánh BN với BC + MN đúng là
A. ;
B. ;
C. ;
D. Không đủ dữ kiện để so sánh.
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
A. Chu vi ∆AFB nhỏ hơn chu vi ∆AMB;
B.Chu vi ∆AFB lớn hơn chu vi ∆AMB;
C.Chu vi ∆AFB bằng chu vi ∆AMB;
D. Không đủ dữ kiện để so sánh.
Cho ∆ABC cân tại A, trên các cạnh AB, AC lần lượt lấy hai điểm P và Q sao cho AP = AQ. Hai đoạn thẳng CP và BQ cắt nhau tại O. OH và OK lần lượt là khoảng cách từ O đến AB và AC. Khẳng định nào dưới đây sai?
A. Tam giác OBC cân;
B. OH ≠ OK;
C. AO là tia phân giác góc A;
D. OP = OQ.
Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
A. Trung trực của EF đi qua A;
B. BE + CF = BC;
C. ;
D. Cả A, B và C đều sai.
Cho ∆ABC nhọn có đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng nhất.
A. ∆AIK cân tại A;
B.∆AIK vuông cân tại A;
C.∆AIK đều;
D.∆AIK vuông tại A.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải