10 câu hỏi
Trong các vectơ sau, vectơ nào sau đây có điểm đầu là A, điểm cuối là B?
\(\overrightarrow {AA} \);
\(\overrightarrow {BA} \);
\(\overrightarrow {AB} \);
\(\overrightarrow {BB} \).
Trong không gian cho 3 điểm phân biệt A, B, C. Vectơ nào trong các vectơ sau đây là vectơ – không?
\(\overrightarrow {BB} \);
\(\overrightarrow {BA} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {CA} \).
Cho hình hộp chữ nhật ABCD.A'B'C'D'.
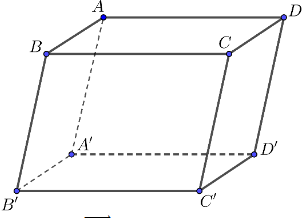
Vectơ nào sau đây cùng phương với \(\overrightarrow {BC} \).
\(\overrightarrow {DC} \);
\(\overrightarrow {DA} \);
\(\overrightarrow {BB'} \);
\(\overrightarrow {C'C} \).
Cho hình hộp chữ nhật ABCD.A'B'C'D'.

Vectơ \(\overrightarrow {BA} \) bằng với vectơ nào sau đây?
\(\overrightarrow {A'B'} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {AB} \).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, vectơ nào sau đây bằng vectơ \(\overrightarrow {AB} \)?
\(\overrightarrow {DC} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {AD} \);
\(\overrightarrow {BC} \).
Cho hình lăng trụ ABC.A'B'C'. Số vectơ khác vectơ – không bằng vectơ \(\overrightarrow {AA'} \) có điểm đầu và điểm cuối là các đỉnh của hình lăng trụ là
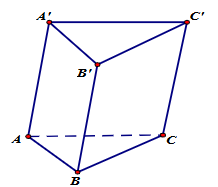
1;
2;
3;
4.
Cho tứ diện ABCD, gọi I là trung điểm của đoạn thẳng AB. Vectơ \(\overrightarrow {AI} \) cùng hướng với vectơ nào sau đây?
\(\overrightarrow {BI} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {CI} \);
\(\overrightarrow {AB} \).
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD?
12;
4;
10;
8.
Trong không gian, cho hình hộp ABCD.A'B'C'D'. Vectơ đối của vectơ \(\overrightarrow {AA'} \) là:
\(\overrightarrow {A'C'} \);
\(\overrightarrow {BA'} \);
\(\overrightarrow {BB'} \);
\(\overrightarrow {C'C} \).
Cho tứ diện ABCD. Các vectơ có điểm đầu là A và điểm cuối là các đỉnh còn lại của hình tứ diện là
\(\overrightarrow {AB} ;\overrightarrow {CA} ;\overrightarrow {AD} \);
\(\overrightarrow {BA} ;\overrightarrow {AC} ;\overrightarrow {AD} \);
\(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {DA} \);
\(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} \).
