10 câu hỏi
Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây sai?
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \];
\[\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\];
\[\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\];
\[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\].
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây đúng?
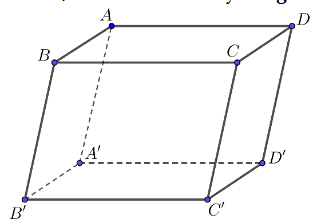
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {AC} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {BD} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {AC'} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {CA} \].
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD và BC. Tổng \(\overrightarrow {AB} + \overrightarrow {DC} \) bằng
\[\overrightarrow 0 \];
\[2\overrightarrow {AD} \];
\[2\overrightarrow {MN} \];
\[2\overrightarrow {NM} \].
Cho hình lăng trụ tam giác ABC.A'B'C'. Đặt \(\overrightarrow {AA'} = \overrightarrow a ;\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c ;\overrightarrow {BC} = \overrightarrow d \). Trong các biểu thức vectơ sau đây, biểu thức nào đúng?
\[\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \];
\[\overrightarrow a = \overrightarrow b + \overrightarrow c \];
\[\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \];
\[\overrightarrow b - \overrightarrow c + \overrightarrow d = \overrightarrow 0 \].
Cho tứ diện ABCD có trọng tâm G, gọi M là trung điểm AD. Khi đó:
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MA} + \overrightarrow {MD} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MB} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} - \overrightarrow {MD} } \right)\].
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của các cạnh AB và CD. Đặt \(\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c ;\overrightarrow {AD} = \overrightarrow d \). Khẳng định nào sau đây đúng?
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow d + \overrightarrow b } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow d + \overrightarrow b - \overrightarrow c } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow b - \overrightarrow d } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow d - \overrightarrow b } \right)\].
Cho hình lăng trụ ABC.A'B'C'. Đặt \(\overrightarrow {AA'} = \overrightarrow a ;\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c \). Gọi G' là trọng tâm của tam giác A'B'C'. Vectơ \(\overrightarrow {AG'} \) bằng?
\[\frac{1}{3}\left( {\overrightarrow a + 3\overrightarrow b + \overrightarrow c } \right)\];
\[\frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\];
\[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + 3\overrightarrow c } \right)\];
\[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
Cho hình lập phương ABCD.A'B'C'D'. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
Cho tứ diện ABCD. Điểm N xác định bởi đẳng thức sau \(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AC} - \overrightarrow {AD} \). Mệnh đề nào đúng?
N là trung điểm BD;
N là đỉnh hình bình hành BCDN;
N là đỉnh hình bình hành CDBN;
N ≡ A.
Cho tứ diện S.ABC có M, N, P là trung điểm của SA, SB, SC. Tìm khẳng định đúng?
\[\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\];
\[\overrightarrow {AB} = \overrightarrow {PN} - \overrightarrow {PM} \];
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PM} - \overrightarrow {PN} } \right)\];
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\].
