10 CÂU HỎI
Giao của ba đường cao trong một tam giác có tên gọi là gì?
A. Trực tâm của tam giác;
B. Trọng tâm của tam giác;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Hãy chọn khẳng định đúng trong các khẳng định sau:
A. Trực tâm của một tam giác luôn nằm ngoài tam giác;
B. Trực tâm của một tam giác luôn nằm trong tam giác;
C. Trực tâm của một tam giác luôn trùng với một đỉnh của tam giác;
D. Cả A, B, C đều sai.
Cho ∆ABC vuông tại B. Điểm nào là trực tâm của ∆ABC?
A. điểm B;
B. điểm C;
C. điểm A;
D. Không xác định được.
Cho hình vẽ
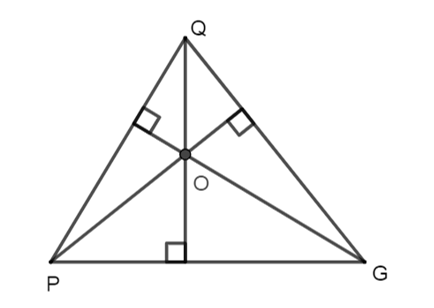
Các đường cao của ∆PQG cắt nhau tại O thì
A. điểm O là trọng tâm của ∆PQG;
B. điểm O là trực tâm của ∆PQG;
C. điểm O cách đều ba cạnh của ∆PQG;
D. điểm O cách đều ba đỉnh của ∆PQG.
Cho ∆ABC cân tại A, đường trung tuyến AD và đường cao BK cắt nhau tại E. Khẳng định nào dưới đây là đúng?
A. AD ⊥ BC;
B. E là trực tâm của ∆ABC;
C. CE⊥ AB;
D. Cả A, B, C đều đúng.
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Điểm nào là trực tâm của tam giác MIK?
A. J;
B. N;
C. K;
D. M.
Cho ∆ABC vuông cân tại A, lấy E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Trực tâm của ∆BCD là điểm nào?
A. E;
B. D;
C. B;
D. C.
Quan sát hình vẽ dưới đây.
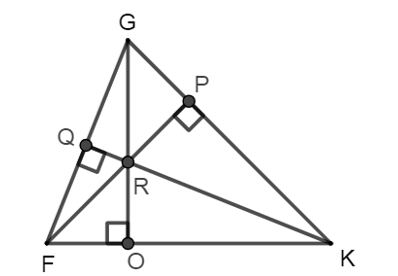
Khẳng định nào dưới đây là sai?
A. Trực tâm của ∆FRK là G;
B. Trực tâm của ∆FPK là O;
C. Trực tâm của ∆GFK là R;
D. Cả A và C đều đúng.
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
A. M là trực tâm của ∆DBC;
B. DM ⊥ BC;
C. M, N, D thẳng hàng;
D. AB, MN, CP không đồng quy.
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
A. MH⊥BC;
B. H là trực tâm tam giác MBC;
C. MH = HC;
D. Cả A, B, C đều sai.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải