10 CÂU HỎI
Vận tốc của một vật chuyển động là v(t) = 3t2 + 5 (m/s). Quãng đường vật đó đi được từ giây thứ 4 đến giây thứ 10 là
A. 669 m;
B. 696 m;
C. 699 m;
D. 966 m.
Một vật chuyển động với gia tốc a(t) = 2cost (m/s2), biết rằng tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng 0. Tính quãng đường vật đi được từ thời điểm t = 0 (s) đến thời điểm t = π (s).
A. 5 m;
B. 3 m;
C. 2 m;
D. 4 m.
Một ô tô đang chuyển động với vận tốc 24 m/s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động thẳng, chậm dần đều với vận tốc biến thiên theo thời gian được xác định bởi quy luật v(t) = −4t + 24 (m/s) trong đó t là khoảng thời gian tính bằng giây kể từ lúc người lái xe bắt đầu đạp phanh. Quãng đường ô tô đi được từ lúc người lái xe bắt đầu đạp phanh đến khi xe dừng hẳn bằng
A. 42 m;
B. 64 m;
C. 72 m;
D. 50 m.
Một vật chuyển động với vận tốc ban đầu bằng 0, vận tốc biến đổi theo quy luật và có gia tốc a = 0,3 m/s2. Xác định quãng đường vật đó đi được trong 40 phút đầu tiên.
A. 12000 m;
B. 240 m;
C. 864000 m;
D. 3200 m.
Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t giây được cho bởi \(v\left( t \right) = \left\{ \begin{array}{l}t\;\;\;\;\;\;\;\;\;\;\;\;khi\;0 \le t \le 2\\2\;\;\;\;\;\;\;\;\;\;\;\;khi\;2 < t \le 20\\12 - 0,5t\;khi\;20 < t \le 24\end{array} \right.\). Tính quãng đường chuyển động của thang máy.
</>
A. 58 m;
B. 56 m;
C. 42 m;
D. 45 m.
Cho hai quả bóng A, B di chuyển ngược chiều nhau va chạm với nhau. Sau va chạm mỗi quả bóng nảy ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng A nảy ngược lại với vận tốc vA(t) = 8 – 2t (m/s) và quả bóng B nảy ngược lại với vận tốc vB(t) = 12 – 4t (m/s). Tính khoảng cách giữa hai quả bóng sau khi đã dừng hẳn (giả sử hai quả bóng đều chuyển động thẳng).
A. 36 m;
B. 32 m;
C. 34 m;
D. 30 m.
Một chiếc máy bay chuyển động trên đường băng với vận tốc v(t) = t2 + 10t (m/s) với t là thời gian tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 m/s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là
A. \(\frac{{2500}}{3}\) m;
B. 2000 m;
C. 500 m;
D. \(\frac{{4000}}{3}\) m.
Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P'(x) = −0,0004x + 9,3. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm. Khi đó sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 125 đơn vị sản phẩm là
A. 232,325 triệu đồng;
B. 230,315 triệu đồng;
C. 321,385 triệu đồng;
D. 231,375 triệu đồng.
Một ô tô đang đi với vận tốc lớn hơn 72 km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là 72 km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc v(t) = 30 – 2t (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72 km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?
A. 100 m;
B. 150 m;
C. 175 m;
D. 125 m.
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian t (giờ) có đồ thị là một phần của đường parabol có đỉnh I(2; 9) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
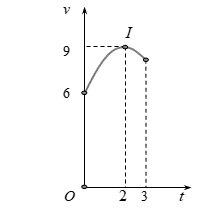
A. s = 25,25 km;
B. s = 24,25 km;
C. s = 24,75 km;
D. s = 26,75 km.

