10 CÂU HỎI
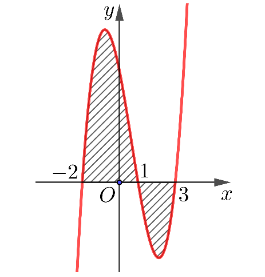
Cho hàm số f(x) liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −2 và x = 3 (như hình vẽ). Mệnh đề nào dưới đây đúng?
A. \(S = - \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} \);
B. \(S = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} \);
C. \(S = - \int\limits_{ - 2}^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} \);
D. \(S = \int\limits_{ - 2}^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} \).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = (x – 2)2 – 1, trục hoành và hai đường thẳng x = 1; x = 2 bằng
A. \(\frac{1}{3}\);
B. \(\frac{2}{3}\);
C. \(\frac{3}{2}\);
D. \(\frac{7}{3}\).
Tính diện tích S hình phẳng giới hạn bởi các đường y = x2 + 1; x = −1; x = 2 và trục hoành.
A. S = 16;
B. S = 6;
C. S = \(\frac{{13}}{6}\);
D. S = 13.
Diện tích S của hình phẳng giới hạn bởi các đường y = 2x2; y = −1; x = 0 và x = 1 được tính bởi công thức nào sau đây?
A. \(S = \pi \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \);
B. \(S = \int\limits_0^1 {\left( {2{x^2} - 1} \right)dx} \);
C. \(S = \int\limits_0^1 {{{\left( {2{x^2} + 1} \right)}^2}dx} \);
D. \(S = \int\limits_0^1 {\left( {2{x^2} + 1} \right)dx} \).
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y = \frac{2}{{x + 1}}\); y = 0; x = 1 và x = 3 là
A. S = ln8;
B. S = ln4;
C. S = 2ln4;
D. S = ln2.
Diện tích hình phẳng S giới hạn bởi các đường thẳng y = x2 – x, y = 0, x = 0, x = 2 được tính bởi công thức nào sau đây?
A. \(S = \int\limits_0^2 {\left( {x - {x^2}} \right)dx} \);
B. \(S = \int\limits_1^2 {\left( {x - {x^2}} \right)dx} - \int\limits_0^1 {\left( {{x^2} - x} \right)dx} \);
C. \(S = - \int\limits_0^1 {\left( {{x^2} - x} \right)dx} + \int\limits_1^2 {\left( {{x^2} - x} \right)dx} \);
D. \(S = \int\limits_0^2 {\left( {{x^2} - x} \right)dx} \).
Hình phẳng giới hạn bởi các đường y = 4 + 2x – x2, y = x2, x = −1, x = 2 có diện tích là
A. 9;
B. 12;
C. 15;
D. 6.
Diện tích hình phẳng giới hạn bởi hai đường y = x3 – x và y = 2x2 – x bằng
A. \(\frac{5}{6}\);
B. \(\frac{1}{2}\);
C. \(\frac{4}{3}\);
D. 2.
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x3 + 11x – 6, y = 6x2 và hai đường thẳng x = 0, x = 2 là
A. S = 2;
B. S = \(\frac{2}{5}\);
C. S = 5;
D. \(S = \frac{5}{2}\).
Tính diện tích phần kẻ sọc trong hình vẽ
A. S = \(\frac{{40}}{3}\);
B. S = \(\frac{{16}}{3}\);
C. S = \( - \frac{{32}}{3}\);
D. \(S = \frac{{32}}{3}\).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
