10 câu hỏi
Hình nào dưới đây biểu diễn góc nội tiếp?
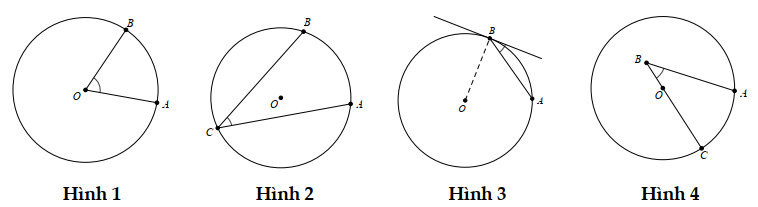
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Góc nội tiếp chắn nửa đường tròn bằng bao nhiêu độ?
45°.
90°.
60°.
120°.
Góc nội tiếp có số đo
bằng hai lần số đo góc ở tâm cùng chắn một cung.
bằng số đo cung bị chắn.
bằng hai lần số đo góc ở tâm cùng chắn một cung.
bằng nửa số đo cung bị chắn.
Cho đường tròn tâm O và hai đường kính AB, CD. Biết rằng \[\widehat {AOC} = 60^\circ \]. Chọn khẳng định sai trong các khẳng định dưới đây.
\[\widehat {BOC} = 120^\circ \].
\[\widehat {ABC} = 60^\circ \].
\[\widehat {ADC} = 30^\circ \].
\[\widehat {BAC} = \widehat {CDB} = 60^\circ \].
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B,C nằm giữa I và D) sao cho \[\widehat {CAB} = 120^\circ \]. Khi đó:
\[\widehat {IAC} = \widehat {CDB} = 70^\circ \].
\[\widehat {IAC} = \widehat {CDB} = 60^\circ \].
\[\widehat {IAC} = 60^\circ ,\widehat {CDB} = 70^\circ .\]
\[\widehat {IAC} = 70^\circ ,\widehat {CDB} = 60^\circ \].
Số đo góc ACM là
100°.
90°.
110°.
100°.
Số đo góc ABM là
90°.
80°.
110°.
120°.
Cho tam giác ABC nhọn nội tiếp đường tròn (O) đường kính BD. Biết \[\widehat {BAC} = 45^\circ \]. Số đo của \[\widehat {CBD}\] là
45°.
60°.
90°.
30°.
Cho tam giác ABC nhọn có \[\widehat {BAC} = 60^\circ \]. Vẽ đường tròn đường kính BC tâm O, cắt AB, AC lần lượt tại D và E. Tính số đo góc \[\widehat {ODE}\].
45°.
60°.
90°.
30°.
Cho tam giác ABC nhọn nội tiếp (O). Trên nửa mặt phẳng bờ BC không chứa A vẽ tia Bx sao cho \[\widehat {xBC} = \widehat A\]. Tính số đo góc OBx.
45°.
60°.
90°.
30°.
