10 câu hỏi
Từ một khúc gỗ hình trụ cao 15 cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là 640π cm3.
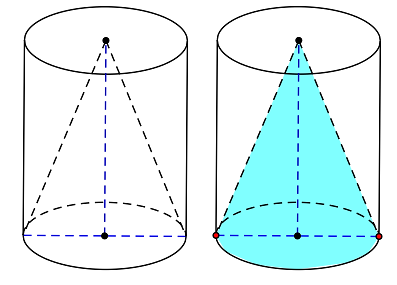
Tính diện tích xung quanh của hình nón.
136π cm2.
120π cm2.
272π cm2.
163π cm2.
Tính diện tích xung quanh của khúc gỗ hình nón.
4π cm2.
\[4\sqrt {2385} \] cm2.
\[4\sqrt {2385} \pi \] cm2.
2385π cm2.
Tính thể tích của khúc gỗ hình trụ.
960π cm3.
720π cm3.
1920π cm3.
1440π cm3.
Một khối đồ chơi gồm một khối hình trụ (T) gắn chồng lên một khối hình nón (N), lần lượt có bán kính đáy và chiều cao tương ứng là r1, h1, r2, h2 thỏa mãn r2 = 2r1, h1 = 2h2 (hình vẽ). Biết rằng thể tích của hình nón (N) bằng 20 cm3.
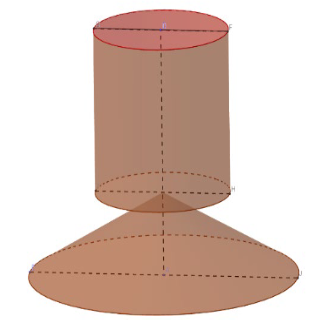
Tính thể tích của toàn bộ khối đồ chơi.
30 cm3.
50 cm3.
60 cm3.
90 cm3.
Tính thể tích phần bị gọt bỏ đi.
36π cm3.
12π cm3.
20π cm3.
24π cm3.
Nếu tăng gấp đôi bán kính R thì thể tích hình trụ (T) và hình nón (N) thay đổi như thế nào?
Thể tích hình nón và hình trụ đều tăng lên 4 lần.
Thể tích hình nón và hình trụ đều tăng lên 2 lần.
Thể tích hình nón tăng 2 lần và thể tích hình trụ tăng 4 lần.
Thể tích hình nón tăng 4 lần và thể tích hình nón tăng 2 lần.
Thể tích của hình nón là
405 cm3.
405π cm3.
324 cm3.
\[324\]π cm3.
Thể tích khối nón bị cắt là
\[\frac{{81}}{2}\] cm3.
162π cm3.
162 cm3.
\[\frac{{81\pi }}{2}\] cm3.
Khối trụ có đáy là hình tròn (I, IB) chiều cao IO nên có thể tích là
\[\frac{{81\pi }}{2}\] cm3.
\[\frac{{243}}{2}\] cm3.
486π cm3.
\[\frac{{243\pi }}{2}\] cm3.
Cho một dụng cụ đựng chất lỏng được tạo bởi một hình trụ và hình nón được lặp đặt như hình bên. Bán kính đáy hình nón bằng bán kính đáy hình trụ. Chiều cao hình trụ bằng chiều cao hình nón và bằng h. Trong bình, lượng chất lỏng có chiều cao bằng \[\frac{1}{{24}}\] chiều cao hình trụ. Lật ngược dụng cụ theo phương vuông góc với mặt đất.
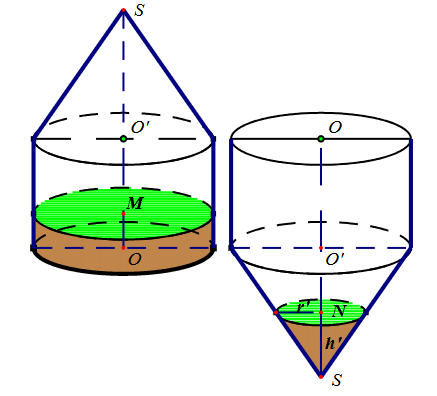
Tính độ cao phần chất lỏng trong hình nón theo h.
h.
\[\frac{h}{3}\].
\[\frac{h}{2}\].
2h.
