10 câu hỏi
Cho hai đường thẳng d và ∆ cắt nhau nhưng không vuông góc với nhau. Mặt tròn xoay sinh bởi đường thẳng d khi quay quanh ∆ là
Mặt trụ.
Mặt phẳng.
Mặt cầu.
Mặt nón.
Quay hình nào dưới đây xung quanh trục đã chỉ ra cho ta một khối nón tròn xoay.
Quay một tam giác cân quanh trục đối xứng với nó.
Quay một tam giác đều quanh một cạnh của nó.
Quay hình chữ nhật ABCD quanh một cạnh của nó.
Quay tam giác ABC vuông tại B xung quanh trục là cạnh AC.
Khi quay một tam giác vuông (kể cả các điểm trong của tam giác vuông đó) quanh đường thẳng chứa một cạnh góc vuông ta được
Hình nón.
Khối trụ.
Khối nón.
Hình trụ.
Một tam giác vuông SOB được quay xung quanh cạnh góc vuông SO, tạo thành một hình nón. Điểm S trên hình nón được gọi là
Đỉnh của hình nón.
Bán kính của hình nón.
Chiều cao của hình nón.
Đường sinh.
Cạnh nào của tam giác trở thành bán kính đáy của hình nón?
Cạnh SO.
Cạnh SB.
Cạnh OB.
Không cạnh nào.
Độ dài SO trong hình nón được gọi là
Đỉnh.
Đường sinh.
Chiều cao.
Bán kính đáy.
Đường sinh của hình nón được hình thành bởi cạnh nào?
Cạnh SO.
Cạnh SB.
Cạnh OB.
Không có cạnh nào.
Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao, bán kính đáy của hình nón. Để tính độ đường sinh của hình nón, ta có:
\[l = \sqrt {{r^2} + {h^2}} \].
\[l = \sqrt {{r^2} - {h^2}} \].
l = r.h.
l = r2 + h2.
Phát biểu nào dưới đây là sai?
Trong hình nón, có vô số đường sinh.
Trong hình nón, đường cao vuông góc với bán kính của đường tròn.
Trong hình nón, chỉ có một đường tròn đáy.
Trong hình nón, có vô số đỉnh.
Cho hình vẽ dưới đây.
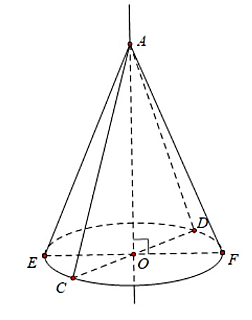
Chọn phát biểu đúng: Hình nón trên được tạo ra
khi quay ∆AOC một vòng xung quanh đường thẳng cố định chứa cạnh AO.
khi quay ∆CAD một vòng xung quanh đường thẳng cố định chứa cạnh CD.
khi quay ∆DOD một vòng xung quanh đường thẳng cố định chứa cạnh AD.
khi quay ∆AEF một vòng xung quanh đường thẳng cố định chứa cạnh EF.
