10 câu hỏi
Cho hình trụ có chu vi đáy là 8π và chiều cao h = 10. Tính thể tích hình trụ.
80π.
40π.
160π.
150π.
Cho hình trụ có bán kính đáy r = 3 (cm) và chiều cao h = 6 (cm). Diện tích xung quanh của hình trụ là
40π.
36π.
18π.
24π.
Cho hình trụ có bán kính r = 12 (cm) và diện tích toàn phần 672π (cm2). Tính chiều cao của hình trụ.
16 cm.
18 cm.
8 cm.
10 cm.
Chọn câu đúng. Cho hình trụ có bán kính r và chiều cao h. Nếu ta giảm chiều cao đi 9 lần và tăng bán kính đáy lên 3 lần thì
Thể tích hình trụ không đổi.
Diện tích toàn phần không đổi.
Diện tích xung quanh không đổi.
Chu vi đáy không đổi.
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 10 (cm) và đường kính đáy là d = 6 cm. Tính diện tích toàn phần của hộp sữa.
110π (cm2).
129π (cm2).
96π (cm2).
69π (cm2).
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25π cm2 và chiều cao h = 10 cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
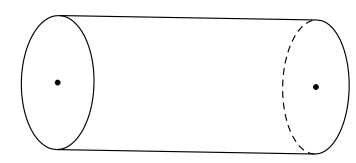
1200π (cm2).
600π (cm2).
1000π (cm2).
1210π (cm2).
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là 3 cm.
7 cm.
5 cm.
3 cm.
9 cm.
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là 4 cm.
2 cm.
4 cm.
1 cm.
8 cm.
Cho hình trụ bị cắt bỏ một phần OABB'A'O' như hình vẽ.
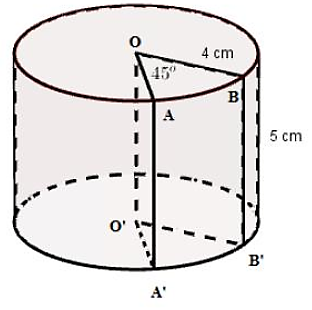
Thể tích phần còn lại là
70π (cm3).
30π (cm3).
60π (cm3).
10π (cm3).
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E. Biết BC = 25 cm và AH = 12 cm. Hãy tính diện tích xung quanh của hình tạo bởi khi cho tứ giác ADHE quay quanh AD.
>
\[\frac{{3456}}{5}\pi \] cm2.
\[\frac{{3456}}{{25}}\pi \] cm2.
\[\frac{{1728}}{{25}}\pi \] cm2.
\[\frac{{7128}}{{25}}\pi \] cm2.
