Quiz

10 bài tập Tìm giá trị nhỏ nhất và lớn nhất của hàm số khi biết đồ thị hàm số hoặc bảng biến thiên có lời giải

Admin10 câu hỏiToánLớp 12

10 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho hàm số f(x) liên tục trên đoạn [−2; 3] có đồ thị như hình vẽ dưới đây.

Cho hàm số f(x) liên tục trên đoạn [−2; 3] có đồ thị như hình vẽ dưới đây. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2; 3] . Giá trị của 2m – 3M bằng: (ảnh 1)

Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2; 3] . Giá trị của 2m – 3M bằng:

A. −13;

B. −18;

C. −16;

D. −15.

2. Nhiều lựa chọn

Cho hàm số y = f(x) liên tục trên đoạn [−1; 3] và có đồ thị như hình vẽ bên.

Cho hàm số y = f(x) liên tục trên đoạn [−1; 3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [−1; 3]. Giá trị của M + m là (ảnh 1)

Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [−1; 3]. Giá trị của M + m là

A. 2;

B. −6;

C. −5;

D. −2.

3. Nhiều lựa chọn

Cho hàm số f(x) liên tục trên đoạn [0; 3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên [0; 3]. Giá trị của M + m bằng?

Cho hàm số f(x) liên tục trên đoạn [0; 3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên [0; 3]. Giá trị (ảnh 1)

A. 5;

B. 3;

C. 2;

D. 1.

4. Nhiều lựa chọn

Cho hàm số y = f(x) liên tục trên đoạn [−1; 5] và có đồ thị như hình vẽ sau:

Cho hàm số y = f(x) liên tục trên đoạn [−1; 5] và có đồ thị như hình vẽ sau: Khẳng định nào sau đây đúng? (ảnh 1)

Khẳng định nào sau đây đúng?

A. \[\mathop {Max}\limits_{\left[ { - 1;5} \right]} f\left( x \right) = 2\];

B. \[\mathop {Min}\limits_{\left[ {3;5} \right]} f\left( x \right) = - 2\];

C. \[\mathop {Max}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 3\];

D. \[\mathop {Max}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 1\].

5. Nhiều lựa chọn

Giá trị lớn nhất của hàm số $y = \left\{ \begin{array}{l} - {x^2} + 3, - 2 \le x \le 0\\3 - x{\rm{ }},0 < x \le 3\\x - 3{\rm{ }},3 < x \le 7\end{array} \right.$ có đồ thị như hình là

$Giá trị lớn nhất của hàm số $y = \left\{ \begin{array}{l} - {x^2} + 3, - 2 \le x \le 0\\3 - x{\rm{ }},0 < x \le 3\\x - 3{\rm{ }},3 < x \le 7\end{array} \right.$ có đồ thị như hình là (ảnh 1)$

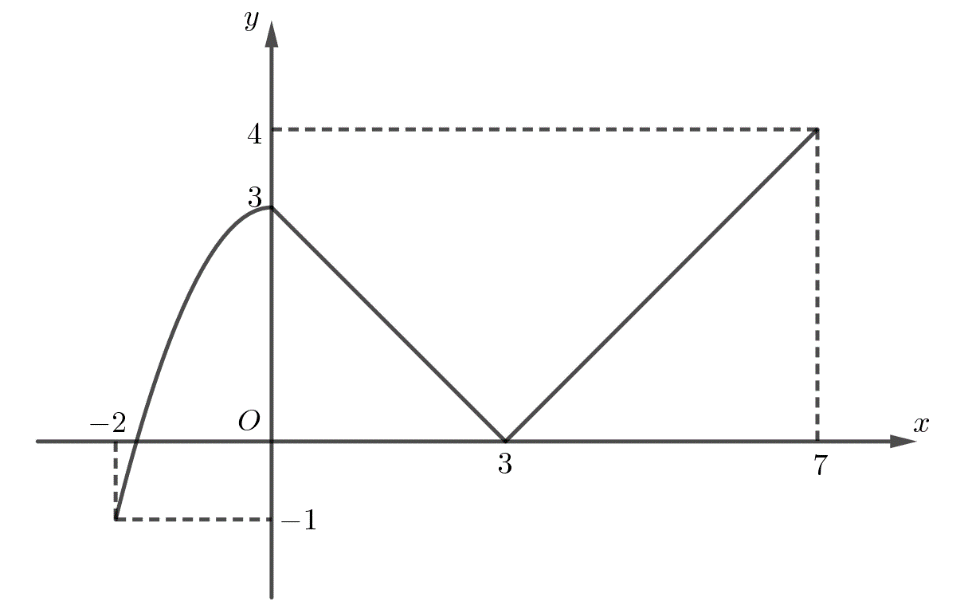
A. 3

A. 3;

B. 7;

C. −1;

D. 4.

6. Nhiều lựa chọn

Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình vẽ.

Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau: (ảnh 1)

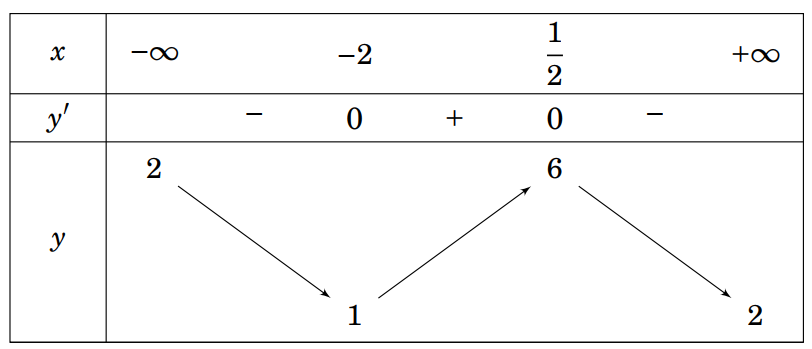
Chọn khẳng định đúng trong các khẳng định sau:

A. Giá trị nhỏ nhất của hàm số y = f(x) trong khoảng (−∞; −2) là 1;

B. Giá trị lớn nhất của hàm số y = f(x) trong khoảng $\left( { - \infty ;\frac{1}{2}} \right)$ là 6;

C. Giá trị nhỏ nhất của hàm số y = f(x) trong khoảng $\left( { - 2;\frac{1}{2}} \right)$ là 1;

D. Hàm số y = f(x) không có giá trị nhỏ nhất trên khoảng (−2; +∞).

7. Nhiều lựa chọn

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Hãy chọn khẳng định đúng?

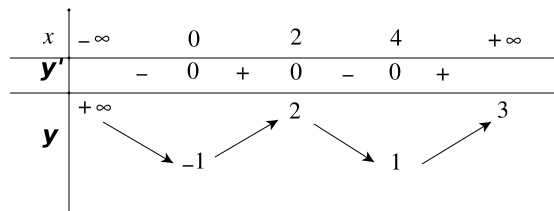
A. Hàm số có giá trị lớn nhất bằng 3 và giá trị nhỏ nhất bằng −1.

B. Hàm số có giá trị lớn nhất bằng 3 và giá trị nhỏ nhất bằng 1.

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng −1.

D. Không tồn tại giá trị lớn nhất của hàm số.

8. Nhiều lựa chọn

Cho hàm số y = f(x) xác định và liên tục trên đoạn [−4; 5], có bảng biến thiên

Cho hàm số y = f(x) xác định và liên tục trên đoạn [−4; 5], có bảng biến thiên Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) xác định trên đoạn [−4; 5]. Tính M + (ảnh 1)

Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) xác định trên đoạn [−4; 5]. Tính M + N?

A. $ - \frac{{16}}{3}$;

B. \[ - \frac{{50}}{3}\];

C. 2;

D. −20.

9. Nhiều lựa chọn

Cho hàm số y = f(x) liên tục trên [−3; 2] và có bảng biến thiên như hình dưới đây. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [−1; 2]. Giá trị của M + m bằng bao nhiêu ?

Cho hàm số y = f(x) liên tục trên [−3; 2] và có bảng biến thiên như hình dưới đây. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [−1; 2]. Giá trị của M (ảnh 1)