10 câu hỏi
Công thức biểu thị số đo của các góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo bằng 120° là
–120° + k360° (k ∈ ℤ);
120° + k360° (k ∈ ℤ);
120° + k180° (k ∈ ℤ);
–120° + k180° (k ∈ ℤ).
Cho góc hình học uOv = 45°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
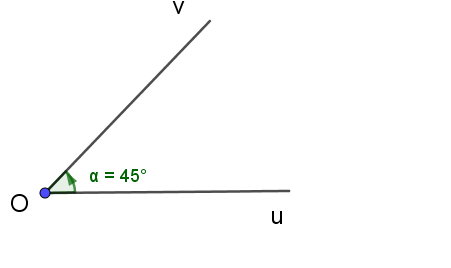
60°;
– 45°;
45°;
– 60°.
Cho góc hình học uOv = 75°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
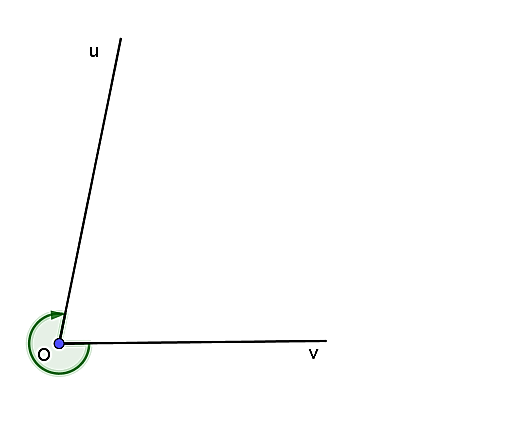
315°;
–315°;
285°;
–285°.
Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
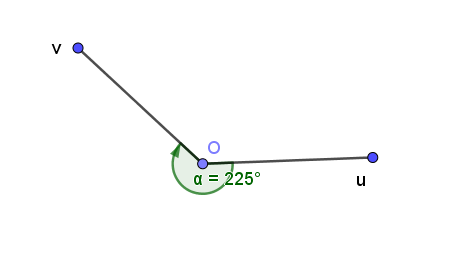
225°;
–225°;
135°;
–135°.
Cho góc lượng giác (OA, OB) có số đo bằng \(\frac{\pi }{5}\). Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
A. \(\frac{{6\pi }}{5}\);
B. \(\frac{{ - 11\pi }}{5}\);
C. \(\frac{{9\pi }}{5}\);
\(\frac{{31\pi }}{5}.\)
Cho góc lượng giác (OA, OB) có số đo 395°. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
45°;
–35°;
35°;
–45°.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 30 phút, kim phút quét một góc lượng giác bằng
A. – 900°;
B. – 1 000°;
C. 900°;
– 1 000°.
Các góc lượng giác (Ox, Ou) và (Ox, Ov) có số đo lần lượt là –270° và 135°. Số đo của góc lượng giác (Ou, Ov) là
50° + m360°, m ∈ ℤ;
45° + m360°, m ∈ ℤ;
–45° + m360°, m ∈ ℤ;
–50° + m360°, m ∈ ℤ.
Cho góc lượng giác (Ou, Ov) có số đo là \(\frac{{3\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{5\pi }}{4}\). Số đo của góc lượng giác (Ov, Ow) là
\(\frac{{ - \pi }}{2}\) + k2π (k ∈ ℤ);
\(\frac{\pi }{2}\) + k2π (k ∈ ℤ);
\(\frac{{ - \pi }}{3}\) + k2π (k ∈ ℤ);
\(\frac{\pi }{3}\) + k2π (k ∈ ℤ).
Cho góc lượng giác (Ou, Ov) có số đo là \(\frac{{ - 5\pi }}{4}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{15\pi }}{4}\). Tìm số đo của góc lượng giác (Ov, Ow) biết rằng 4π < sđ (Ov, Ow) < 6π.
</>
4π;
7π;
5π;
6π.
