10 CÂU HỎI
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
A.
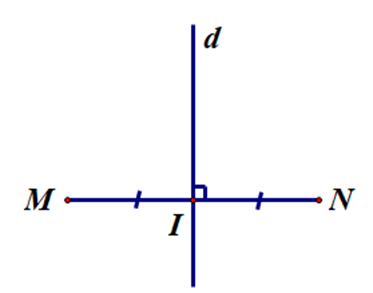
B.
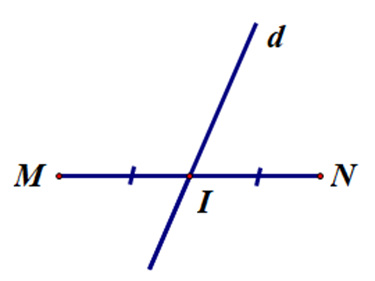
C.
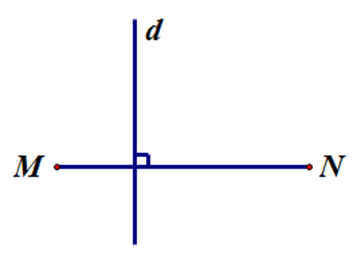
D.
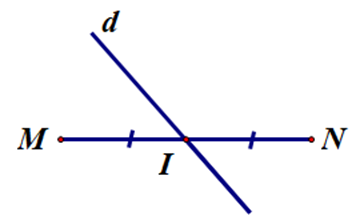
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
A. AD vuông góc với BC;
B. AD vuông góc với BE;
C. AD là đường trung trực của đoạn thẳng BE;
D. AD đi qua trung điểm của đoạn thẳng BE.
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\], lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
A.Ot vuông góc với AB;
B.Ot là đường trung trực của đoạn thẳng AB;
C. Ot đi qua trung điểm của AB;
D. \[\widehat {OAI} \ne \widehat {OBI}\].
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
A. AM là đường trung trực của đoạn thẳng BC;
B. AN là đường trung trực của đoạn thẳng BC;
C. MN là đường trung trực của đoạn thẳng BC;
D. Cả A, B, C đều đúng.
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
A. \[\widehat {ADC} = \widehat {ACD}\];
B. AK ⊥ DC;
C. AK là đường trung trực của đoạn thẳng DC;
D. Cả A, B, C đều đúng.
Cho ∆ABC cân tại A, đường phân giác trong của \[\widehat A\] cắt BC tại D. Khẳng định nào dưới đây sai?
A. AD là đường trung trực của BC;
B. \[\widehat {ABC} + \widehat {CAD} = 90^\circ \];
C. ∆ADB = ∆ADC;
D. \[\widehat {ABC} + \widehat {ADC} = 180^\circ \].
Cho đoạn thẳng AB. Dựng các ∆PAB cân tại P, ∆QAB cân tại Q (P, Q nằm khác phía so với AB). Khẳng định nào sau đây là đúng nhất?
A. P thuộc đường trung trực của AB;
B. Q thuộc đường trung trực của AB;
C. PQ là đường trung trực của AB;
D. \[\widehat {PAB} > \widehat {PBA}\].
Cho \[\widehat {xOy}\] (\[0^\circ < \widehat {xOy} < 90^\circ \]), Ot là tia phân giác của \[\widehat {xOy}\] và H là một điểm bất kỳ thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C và d’ vuông góc với Oy tại B, cắt Ox tại D. Khẳng định nào sau đây sai?
A. OH là đường trung trực của đoạn thẳng AB;
B. OC > OD;
C. OH là đường trung trực của đoạn thẳng CD;
D. OA = OB.
Cho ∆DEF cân tại D. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc với DF (Q ∈ DF). Khẳng định nào sau đây sai?
A. K thuộc đường trung trực của EF;
B. K thuộc đường trung trực của PQ;
C. DK là đường trung trực của EF;
D. DK không là đường trung trực của PQ.
Cho hình bên.
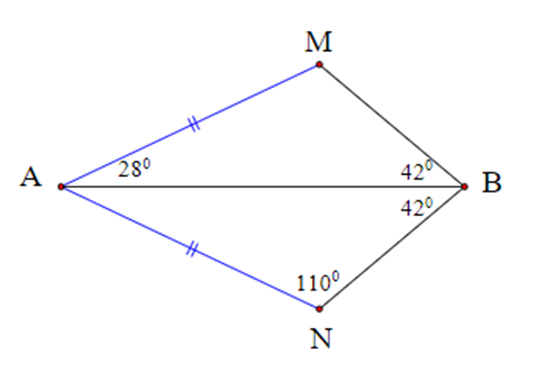
Chọn kết luận sai.
A. A thuộc đường trung trực của MN;
B. B thuộc đường trung trực của MN;
C. AB là đường trung trực của MN;
D. AB không là đường trung trực của MN.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải