(Trả lời ngắn) 35 bài tập Đường tiệm cận của đồ thị hàm số (có lời giải)

Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số \[y = \frac{{3x - 7}}{{x + 2}}\] là

Đồ thị hàm số \(y = \frac{{x - 1}}{{x + 2}}\) có tiệm cận đứng là đường thẳng

Đồ thị hàm số \(y = \frac{{2x + 2}}{{{x^2} - 1}}\) có bao nhiêu đường tiệm cận?

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ

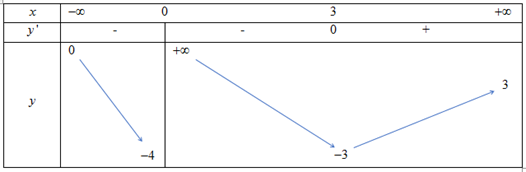
Tổng số đường tiệm cận đứng và ngang của đồ thị đã cho bằng

Đường thẳng \(y = \frac{1}{3}\) là tiệm cận ngang của đồ thị hàm số

Đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây?

Tiệm cận ngang của đồ thị hàm số \[y = \frac{{3x - 5}}{{4x - 8}}\] là

Tiệm cận ngang của đồ thị hàm số \[y = \frac{3}{{2x - 1}}\] là

Tìm phương trình đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 2}}\).

Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \[y = \frac{{9 - 6x}}{{3x + 12}}\]

Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}\).

Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 5}}\).

Tìm tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 2x + 1}}{{x + 1}}\).

Cho hàm số \(y = f\left( x \right) = x + \frac{1}{{x + 2}}\). Tìm tiệm cận xiên của đồ thị hàm số \(f\left( x \right)\).

Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - x + 2}}{{x + 1}}\).

Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{x + 1}}{{x - 2}}\).

Tìm tiệm cận đứng, ngang, xiên (nếu có) của đồ thị mỗi hàm số sau:

a) \(y = \frac{x}{{2 - x}}\)

b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\) 

c) \(y = x - 3 + \frac{1}{{{x^2}}}\)

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau. Hỏi đồ thị hàm số đó có mấy tiệm cận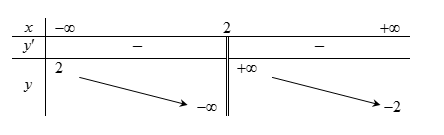

Cho hàm số \[y = \sqrt {4x - {x^2}} \], tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là

Số đường tiệm cận của đồ thị hàm số \(y = \frac{{2x - 1}}{{{x^2} - 3x + 2}}\) là

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{{x^2} - 3x + 2}}{{{x^2} - 1}}\) là

Số đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt {1 - x} }}{{{x^2} - 4}}\) là

Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{1 - 4x}}{{2x - 1}}\)?

Tìm số đường tiệm cận của đồ thị hàm số \({\rm{y}} = \frac{{2{\rm{x}} - 1}}{{{{\rm{x}}^2} + 1}}\).

Tìm số đường tiệm cận của đồ thị hàm số \({\rm{y}} = \frac{{2{\rm{x}} - 1}}{{{{\rm{x}}^2} + 1}}\).

Đường tiệm cận ngang của đồ thị hàm số \(y = 1 + \frac{{2x + 1}}{{x + 2}}\) có phương trình là:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \[\mathbb{R}\backslash \left\{ 1 \right\}\] có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\)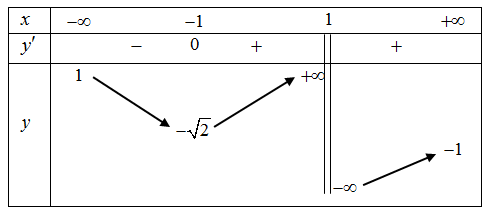

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và ngang?

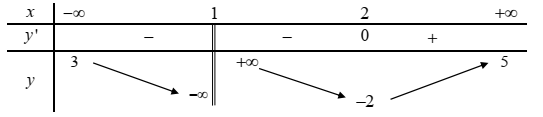
Số đường tiệm cận của đồ thị hàm số \(y = \frac{{x - 3}}{{\sqrt {{x^2} - 9} }}\) là:

Các đường tiệm cận của đồ thị hàm số \[y = \frac{{2x + 1}}{{x - 3}}\] tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

Đồ thị hàm số \(y = \frac{{5x + 1 - \sqrt[{}]{{x + 1}}}}{{{x^2} + 2x}}\) có tất cả bao nhiêu đường tiệm cận?

Đồ thị hàm số 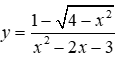có số đường tiệm cận đứng là m  và số đường tiệm cận ngang là n . Giá trị của m + n là

Cho hàm số \[y = \frac{{2x - 1}}{{x + 1}}\,\,\,\,\left( C \right)\]. Biết rằng \[{M_1}\left( {{x_1};{y_1}} \right)\] và \[{M_2}\left( {{x_2};{y_2}} \right)\] là hai điểm trên đồ thị \[\left( C \right)\] có tổng khoảng cách đến hai đường tiệm cận của \[\left( C \right)\] nhỏ nhất. Tính giá trị \[P = {x_1}.{x_2} + {y_1}{y_2}\].

Cho hàm số \(y = \frac{{2x + 1}}{{x - 1}}{\rm{ }}\left( C \right)\). Tính tổng tung độ các điểm \[M\] thỏa mãn \(M\) thuộc đồ thị \(\left( C \right)\) đồng thời khoảng cách từ \[M\] đến tiệm cận đứng của đồ thị \(\left( C \right)\) bằng khoảng cách từ \[M\] đến trục \[Ox\]