Quiz

ĐGTD ĐH Bách khoa - Tư duy Toán học - Mặt cầu ngoại tiếp, nội tiếp

VietJackĐH Bách KhoaĐánh giá năng lực8 lượt thi

Bắt đầu ngay

33 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Khối cầu thể tích V thì bán kính là:

$R = \frac{3 V}{4 π}$

$R = \sqrt{\frac{3 V}{4 π}}$

$R = \frac{1}{2} . \sqrt[3]{\frac{3 V}{π}}$

$R = \sqrt[3]{\frac{3 V}{4 π}}$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Công thức tính diện tích mặt cầu là:

$S = π R^{2}$

$S = 4 π R^{2}$

$S = 2 π R^{2}$

$\frac{4}{3} π R^{2}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:

$R = \sqrt{r^{2} + \frac{h^{2}}{4}}$

$R = \sqrt{r^{2} + \frac{h^{2}}{2}}$

$R = \sqrt{r^{2} - \frac{h^{2}}{4}}$

$R = r^{2} + \frac{h^{2}}{4}$

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho một mặt cầu bán kính bằng 1. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?

$\min V = 4 \sqrt{3}$

$\min V = 8 \sqrt{3}$

$\min V = 9 \sqrt{3}$

$\min V = 16 \sqrt{3}$

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho một lập phương có cạnh bằng a. Tính diện tích mặt cầu nội tiếp hình lập phương đó

$S = 4 π a^{2}$

$S = π a^{2}$

$S = \frac{1}{3} π a^{2}$

$S = \frac{4 π a^{2}}{3}$

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối cầu có bán kính R = 6. Thể tích của khối cầu bằng

$144 π$

$36 π$

$288 π$

$48 π$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tam giác S.ABC có $\hat{S A C} = \hat{S B C} = 90^{0}$ . Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên b. Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:

$\frac{b^{2}}{2 \sqrt{b^{2} - \frac{a^{2}}{2}}}$

$\frac{b^{2}}{\sqrt{b^{2} - \frac{a^{2}}{2}}}$

$\frac{b^{2}}{2 \sqrt{b^{2} - \frac{a^{2}}{4}}}$

$\frac{2 b^{2}}{\sqrt{b^{2} - \frac{a^{2}}{2}}}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Ba đoạn thẳng SA, SB, SC đôi một vuông góc tạo với nhau thành một tứ diện SABC với SA = a, SB = 2a, SC = 3a . Tính bán kính mặt cầu ngoại tiếp hình tứ diện đó là

$\frac{a \sqrt{6}}{2}$

$\frac{a \sqrt{3}}{6}$

$\frac{a \sqrt{14}}{2}$

$\frac{a \sqrt{14}}{4}$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình chóp S.ABC có đáy ABC là tam giác vuông tại A có SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b, AC = c. Mặt cầu đi qua các đỉnh A,B,C,S có bán kính r bằng :

$\frac{2 (a + b + c)}{3}$

$2 \sqrt{a^{2} + b^{2} + c^{2}}$

$\frac{1}{2} \sqrt{a^{2} + b^{2} + c^{2}}$

$\sqrt{a^{2} + b^{2} + c^{2}}$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện đều ABCD có cạnh a. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:

$\frac{a \sqrt{6}}{12}$

$\frac{a \sqrt{6}}{6}$

$\frac{a \sqrt{6}}{3}$

$\frac{a \sqrt{6}}{8}$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, AB = AC = a, AA’ = $a \sqrt{2}$ . Diện tích mặt cầu ngoại tiếp tứ diện CA′B′C′ là:

$\frac{4 π a^{2}}{3}$

$4 π a^{2}$

$12 π a^{2}$

$4 \sqrt{3} π a^{2}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là 2;2;1. Tìm bán kính R của mặt cầu ngoại tiếp hình hộp chữ nhật trên.

R = 3

$R = \frac{3}{2}$

$\frac{9}{2}$

$R = 9$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho mặt cầu (S₁) có bán kính R₁ mặt cầu (S₂) có bán kính R₂ = 2R₁. Tính tỉ số diện tích của mặt cầu (S₂) và (S₁).

12.

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

$V = \frac{5 \sqrt{15} π}{18}$

$V = \frac{5 \sqrt{15} π}{54}$

$V = \frac{4 \sqrt{3} π}{27}$

$V = \frac{5 π}{3}$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh $S A = \frac{2 a \sqrt{3}}{3}$ . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABD

$R = \frac{a \sqrt{39}}{7}$

$R = \frac{a \sqrt{35}}{7}$

$R = \frac{a \sqrt{37}}{6}$

$R = \frac{a \sqrt{13}}{7}$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, $S A ⊥ (A B C D)$ và SA = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.

$9 π a^{3}$

$\frac{9 π a^{3}}{2}$

$\frac{9 π a^{3}}{8}$

$36 π a^{3}$

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có $S A ⊥ (A B C); A C = b, A B = c, \hat{B A C} = α$ . Gọi B′,C′ lần lượt là hình chiếu vuông góc của A lên SB,SC. Tính bán kính mặt cầu ngoại tiếp khối chóp A.BCC′B′ theo b,c, $α$

$R = 2 \sqrt{b^{2} + c^{2} - 2 b c \cos α}$

$R = \frac{\sqrt{b^{2} + c^{2} - 2 b c \cos α}}{\sin 2 α}$

$R = \frac{\sqrt{b^{2} + c^{2} - 2 b c \cos α}}{2 \sin α}$

$R = \frac{2 \sqrt{b^{2} + c^{2} - 2 b c \cos α}}{\sin α}$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD có AB = a;AC = BC = AD = BD = $\frac{a \sqrt{3}}{2}$ . Gọi M,N là trung điểm của AB,CD. Góc giữa hai mặt phẳng (ABD);(ABC) là $α$ . Tính $c o s α$ biết mặt cầu đường kính MN tiếp xúc với cạnh AD.

$2 - \sqrt{3}$

$2 \sqrt{3} - 3$

$3 - 2 \sqrt{3}$

$\sqrt{2} - 1$

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại BB có cạnh $A B = 3, B C = 4$ và góc giữa DC và mặt phẳng (ABC) bằng 45⁰. Tính thể tích mặt cầu ngoại tiếp tứ diện.

$V = \frac{125 \sqrt{3}}{3} π$

$V = \frac{25 \sqrt{2}}{3} π$

$V = \frac{125 \sqrt{2}}{3} π$

$V = \frac{5 \sqrt{2}}{3} π$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh $2 \sqrt{2}$ . Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3. Mặt phẳng qua A và vuông góc với SC cắt cạnh SB,SC,SD lần lượt tại M,N,P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP.

$V = \frac{32 π}{3}$

$V = \frac{64 \sqrt{2} π}{3}$

$V = \frac{108 π}{3}$

$V = \frac{125 π}{6}$

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có $A A ’ = 2 a, B C = a$ . Gọi M là trung điểm BB’. Bán kính mặt cầu ngoại tiếp khối chóp M.A’B’C’ bằng:

$\frac{3 \sqrt{3} a}{8}$

$\frac{\sqrt{13} a}{2}$

$\frac{\sqrt{21} a}{6}$

$\frac{2 \sqrt{3} a}{3}$

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = 3, AC = 4, BC = 5 và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng

$\frac{7 \sqrt[]{21} π}{2}$

$\frac{4 \sqrt{17} π}{3}$

$\frac{29 \sqrt[]{29} π}{6}$

$\frac{20 \sqrt[]{5} π}{3}$

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai khối cầu (S₁),(S₂) có cùng bán kính 2 thỏa mãn tính chất: tâm của (S₁) thuộc (S₂) và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi (S₁) và (S₂).

$\frac{10 π}{3}$

$3 π$

$\frac{16 π}{5}$

$8 π$

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; $∠ B A C = 120^{0}$ . Tính diện tích mặt cầu ngoại tiếp lăng trụ trên.

$\frac{64 \sqrt{2} π}{3}$

$16 π$

$32 π$

$\frac{32 \sqrt{2} π}{3}$

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Một thùng rượu vang có dạng hình tròn xoay có hai đáy là hai hình tròn bằng nhau, khoảng cách giữa hai đáy bằng 80(cm). Đường sinh của mặt xung quanh thùng là một phần đường tròn có bán kính 60(cm)(tham khảo hình minh họa bên). Hỏi thùng đó có thể đựng bao nhiêu lít rượu?(làm tròn đến hàng đơn vị)

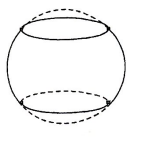
Media VietJack

771

385

603

905

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

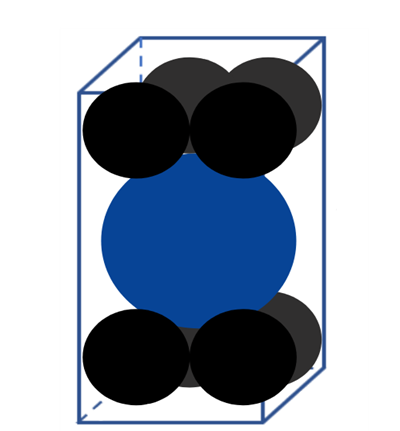
Cho một hình hộp chữ nhật kích thước $4 \times 4 \times h$ chứa một khối cầu lớn có bán kính bằng 2 và 8 khối cầu nhỏ có bán kính bằng 1. Biết rằng các khối cầu đều tiếp xúc với nhau và tiếp xúc với các mặt của hình hộp (tham khảo hình vẽ). Thể tích của khối hộp bằng

Media VietJack

$32 + 32 \sqrt{5}$

$48 + 32 \sqrt{7}$

$32 + 64 \sqrt{2}$

$32 + 32 \sqrt{7}$

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều nn cạnh (n ≥ 3)). Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60⁰ , thể tích khối chóp bằng $\frac{3 \sqrt{3}}{4} R^{3}$ . Tìm n?

n = 4

n = 8

n = 10

n = 6

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho ba hình cầu có bán kính lần lượt là R₁,R₂,R₃ đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng $R_{1} + R_{2} + R_{3}$ :

$\frac{67}{12}$

$\frac{59}{12}$

$\frac{53}{12}$

$\frac{61}{12}$

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Có 4 viên bi hình cầu bán kính bằng 1cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc vởi cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng

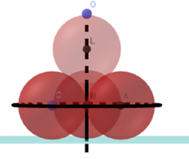
Media VietJack

$\frac{7}{2} .$

$\frac{6 + 2 \sqrt{6}}{3} .$

$\frac{3 + 2 \sqrt{6}}{3} .$

$\frac{4 \sqrt{6}}{3} .$

Xem đáp án

31. Trắc nghiệm

• 1 điểm • Không giới hạn

Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1,2,4. Tổng độ dài đường kính của hai quả bóng đó.

Xem đáp án

32. Trắc nghiệm

• 1 điểm • Không giới hạn

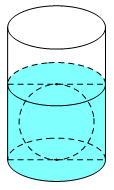
Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5cm. Bán kính của viên billiards đó bằng

Media VietJack

4,2cm.

3,6cm.

2,6cm.

2,7cm.

Xem đáp án

33. Trắc nghiệm

• 1 điểm • Không giới hạn

Một hộp đựng phấn hình hộp chữ nhật có chiều dài 30cm, chiều rộng 5cm và chiều cao 6cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao h=6cm và bán kính đáy $r = \frac{1}{2} c m$ . Hỏi có thể xếp được tối đa bao nhiêu viên phấn.