29 câu hỏi
Cho hàm số y=f(x) có đạo hàm trên (a;b). Nếu \[f\prime (x)\;\] đổi dấu từ âm sang dương qua điểm \[{x_0}\] thuộc (a;b) thì
\[{x_0}\] là điểm cực đại của hàm số.
\[{x_0}\] là điểm cực tiểu của hàm số
\[{x_0}\] là điểm cực đại của đồ thị hàm số.
\[{x_0}\] là điểm cực tiểu của đồ thị hàm số.
Giả sử \[y = f(x)\;\] có đạo hàm cấp hai trên (a;b). Nếu \(\left\{ {\begin{array}{*{20}{c}}{f'\left( {{x_0}} \right) = 0}\\{f''\left( {{x_0}} \right) > 0}\end{array}} \right.\) thì
\({x_0}\) là điểm cực tiểu của hàm số.
\({x_0}\) là điểm cực đại của hàm số.
\({x_0}\) là điểm nằm bên trái trục tung.
\({x_0}\) là điểm nằm bên phải trục tung.
Nếu \[{x_0}\] là điểm cực đại của hàm số thì \[({x_0};f({x_0}))\;\]là:
Giá trị cực đại của hàm số.
Giá trị cực đại của đồ thị hàm số.
Điểm cực đại của hàm số.
Điểm cực đại của đồ thị hàm số.
Nếu \[{x_0}\] là điểm cực tiểu của hàm số thì \[f({x_0})\;\] là:
Giá trị cực tiểu của hàm số.
Giá trị cực đại của hàm số.
Điểm cực tiểu của hàm số.
Điểm cực đại của hàm số.
Điều kiện để hàm số bậc ba không có cực trị là phương trình y′=0 có:
nghiệm kép.
vô nghiệm.
hai nghiệm phân biệt.
Cả A và B đúng.
Cho các phát biểu sau:
1. Hàm số y=f(x) đạt cực đại tại \[{x_0}\] khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua \[{x_0}\].
2. Hàm số y=f(x) đạt cực trị tại \[{x_0}\] khi và chỉ khi \[{x_0}\] là nghiệm của đạo hàm.
3. Nếu \[f\prime (x0) = 0\;\] và \[f\prime \prime (x0) = 0\;\] thì \[{x_0}\] không phải là cực trị của hàm số y=f(x) đã cho.
4. Nếu f′(x0)=0 và \[f\prime \prime (xo) > 0\;\] thì hàm số đạt cực đại tại \[{x_0}\].
Các phát biểu đúng là:
1; 3; 4
1
1; 2; 4
Tất cả đều đúng
Cho hàm số y=f(x)) có bảng biến thiên trên khoảng (0;2) như sau:
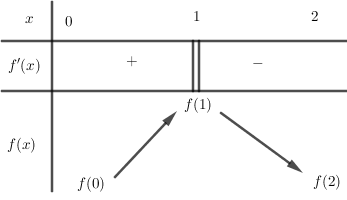
Khẳng định nào sau đây là khẳng định đúng:
Trên (0;2), hàm số không có cực trị
Hàm số đạt cực đại tại x=1
Hàm số đạt cực tiểu tại x=1
Hàm số đạt cực tiểu tại x=0
Cho hàm số y=f(x) có bảng biến thiên như sau:
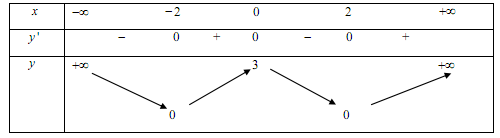
Khẳng định nào sau đây là khẳng định sai:
Hàm số đạt cực tiểu tại x=2
Hàm số đạt cực đại tại x=3
Hàm số đạt cực tiểu tại x=−2
Hàm số đạt cực đại tại x=0
Cho hàm số y=f(x) có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
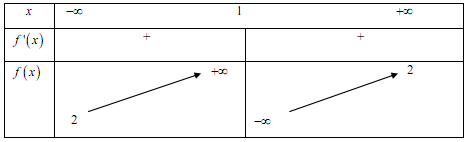
Giá trị cực tiểu của hàm số là y=2
Giá trị cực đại của hàm số là y=2.
Giá trị cực tiểu của hàm số là \[y = - \infty \]
Hàm số không có cực trị.
Cho hàm số y=f(x) có bảng biến thiên như hình bên dưới, chọn khẳng định sai:
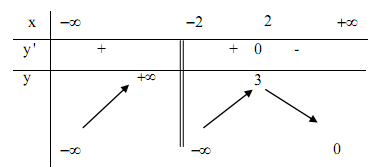
Hàm số đạt cực đại tại x=2
Giá trị cực đại của hàm số là y=3
x=−2 là điểm cực tiểu của hàm số.
Điểm (2;3) là điểm cực đại của đồ thị hàm số.
Cho hàm số y=f(x) có đồ thị như hình vẽ bên.
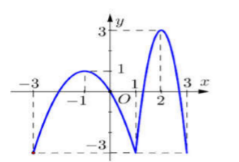
Trên đoạn \[\left[ { - 3;3} \right],\;\]hàm số đã cho có mấy điểm cực trị?
4
5
2
3
Cho hàm số y=f(x) có đồ thị \[f\prime (x)\;\] như hình vẽ. Số điểm cực trị của hàm số y=f(x) là:
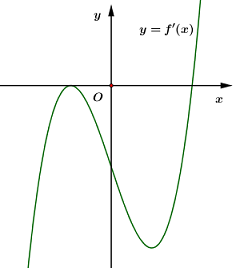
Dựa vào đồ thị hàm số \[y = f'\left( x \right)\] ta thấy \[f'\left( x \right)\] có 1 lần đổi dấu từ âm sang dương
⇒ Hàm số \[y = f\left( x \right)\] có 1 điểm cực trị.
2
3
0
1Trả lời:
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu \[f\prime (x)\;\] như sau :

Hàm số y=f(x) có bao nhiêu điểm cực trị ?
1
2
4
3
Số điểm cực trị của đồ thị hàm số \[y = \frac{{x - 1}}{{2 - x}}\] là:
0
1
2
3
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \[y = {x^3} - 3{x^2} + 1\] là:
y=−2x+1
y=2x−1
y=−2x−1
y=2x+1
Hàm số nào sau đây không có cực trị?
\[y = {x^3}\]
\[y = {x^3} + 3{x^2}\]
\[y = {x^4}\]
\[y = {x^4} + 1\]
Hàm số \[f\left( x \right) = 2\sin 2x - 3\] đạt cực tiểu tại:
\[x = \frac{\pi }{4} + k\pi \]
\[x = \frac{\pi }{4} + \frac{{k\pi }}{2}\]
\[x = \frac{\pi }{2} + k\pi \]
\[x = \frac{\pi }{4} + \frac{{\left( {2k + 1} \right)\pi }}{2}\]
Đồ thị hàm số nào sau đây có 3 điểm cực trị?
\[y = {x^4} + 2{x^2}\]
\[y = {x^4} - 2{x^2} - 1\]
\[y = 2{x^4} + 4{x^2} - 4\]
\[y = - {x^4} - 2{x^2} - 1\]
Cho hàm số y=f(x) có đạo hàm \[f\prime (x) = (x - 1)({x^2} - 2)({x^4} - 4)\] Số điểm cực trị của hàm số y=f(x) là:
3
2
4
1
Đồ thị hàm số \[y = {x^3} - 3x + 2\] có 2 điểm cực trị A,B. Diện tích tam giác OAB với O(0;0) là gốc tọa độ bằng:
2
\(\frac{1}{2}\)
1
3
Hàm số \[y = {x^3} - 3{x^2} + 4\] đạt cực tiểu tại:
x=0
x=2
x=4
x=0 và x=2
Cho hàm số \[y = \frac{{ - {x^2} + 3x + 6}}{{x + 2}}\], chọn kết luận đúng:
Đồ thị hàm số có điểm cực tiểu (−4;11) và điểm cực đại (0;3).
Hàm số có điểm cực tiểu (−4;11) và điểm cực đại (0;3).
Đồ thị hàm số có điểm cực tiểu (0;3) và điểm cực đại (−4;11).
Đồ thị hàm số không có điểm cực trị.
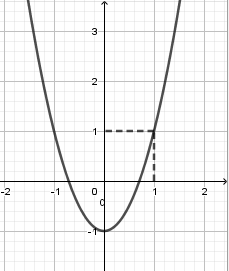
Cho hàm số bậc hai y=f(x) có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm \[g\prime (x) = f(x) + m\]. Tìm tất cả các giá trị thực của tham số m để hàm số g(x) không có cực trị.
A.
B.
m>1 hoặc m<0
m>1
Điểm thuộc đường thẳng \[d:x - y - 1 = 0\] cách đều hai điểm cực trị của đồ thị hàm số \[y = {x^3} - 3{x^2} + 2\;\] là
(2;1).
(0;−1).
(1;0).
(-1;2)
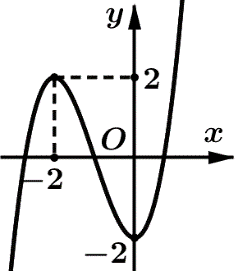
Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\] (với \[a,b,c,d \in \mathbb{R}\;\] và \[a \ne 0\]) có đồ thị như hình vẽ. Số điểm cực trị của hàm số \[g(x) = f( - 2{x^2} + 4x)\;\] là
2.
5.
4.
3.
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
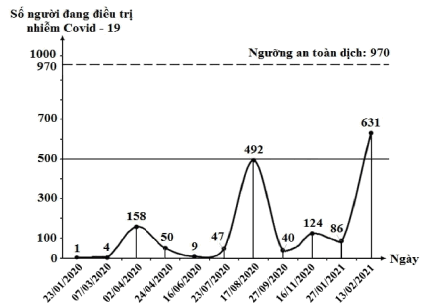
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
16/11/2020.
17/08/2020.
23/07/2020
13/02/2021
Cho hàm số f(x) có bảng biến thiên như sau:
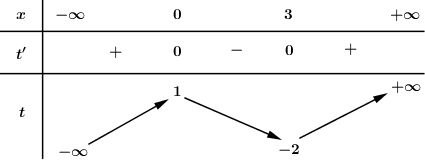
Số điểm cực trị của hàm số \[f({x^2} - 2x)\;\] là:
4
2
5
3
Số điểm cực trị của hàm số \[y = \left| {{x^2} - 3x + 2} \right|\] là:
2
3
1
4
Cho hàm số f(x) có đạo hàm \[f\prime \left( x \right) = {x^2}\left( {x + 2} \right)\left( {x - 3} \right).\] Điểm cực đại của hàm số \[g\left( x \right) = f({x^2} - 2x)\;\] là:
x=3
x=0
x=1
x=−1
