13 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số 
có bảng biến thiên như sau:
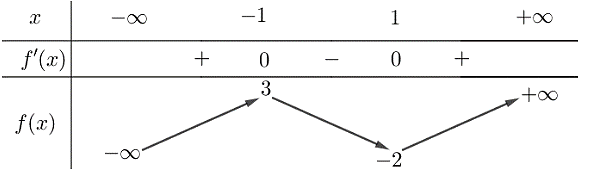
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số 
có bảng biến thiên như sau:
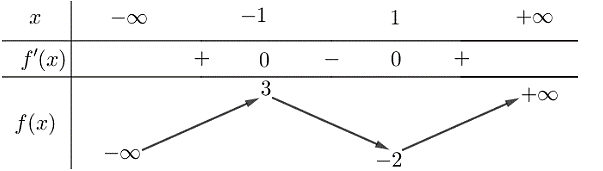
Giá trị cực tiểu của hàm số đã cho bằng
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số 
xác định và liên tục trên 
có đồ thị hàm số như hình vẽ dưới đây.
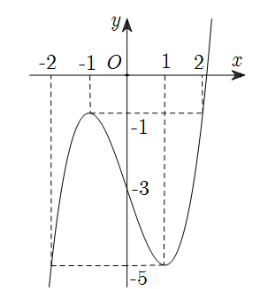
Giá trị nhỏ nhất 
và giá trị lớn nhất 
của hàm số đã cho trên đoạn 
lần lượt là:
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số 
có 
và 
. Phát biểu nào dưới đây là đúng?
Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng 
và 
.
Đồ thị hàm số đã cho không có tiệm cận ngang.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng 
và 
.
Cho tứ diện 
. Có bao nhiêu vectơ khác vectơ 
mà mỗi vectơ có điểm đầu và điểm cuối là hai đỉnh của tứ diện ?
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian với hệ tọa độ 
, cho điểm 
. Tọa độ của vectơ 
là:
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian với hệ tọa độ
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số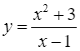 
. Khẳng định nào sau đây là đúng?
Hàm số đã cho đồng biến trên khoảng 
Hàm số đã cho nghịch biến trên khoảng 
.
Hàm số đã cho đồng biến trên khoảng 
.
Hàm số đã cho nghịch biến trên khoảng 
.
Giá trị lớn nhất của hàm số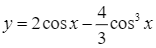 
trên đoạn 
bằng
A. 
.
B. 
.
C. 
.
D. 
.
Tiệm cận xiên của đồ thị hàm số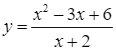 
là đường thẳng:
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số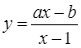 
có đồ thị như hình vẽ dưới đây.
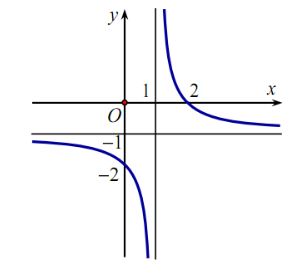
Khẳng định nào sau đây là đúng?
\(b < a < 0\).
\(a < b < 0\).
\(b > a\) và \(a < 0\).
\(a < 0 < b\).
Cho hàm số 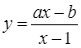có đồ thị như hình vẽ dưới đây.
Khẳng định nào sau đây là đúng?
\(b < a < 0\).
\(a < b < 0\).
\(b > a\) và \(a < 0\).
\(a < 0 < b\).
Cho tứ diện \(ABCD\) và điểm \(G\) thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) (\(G\) là trọng tâm của tứ diện). Gọi \({G_0}\) là giao điểm của \(GA\) và mặt phẳng \(\left( {BCD} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
\(\overrightarrow {GA} = - 2\overrightarrow {{G_0}G} \).
\(\overrightarrow {GA} = 4\overrightarrow {{G_0}G} \).
\(\overrightarrow {GA} = 3\overrightarrow {{G_0}G} \).
\(\overrightarrow {GA} = 2\overrightarrow {{G_0}G} \).