12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên\(\mathbb{R}\), có đồ thị như hình vẽ. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
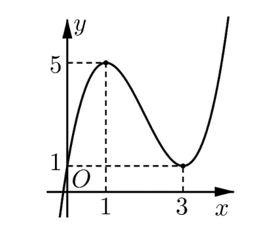
\(\left( {3; + \infty } \right)\).
\(\left( {1;3} \right)\).
\(\left( {0;3} \right)\).
\(\left( {1; + \infty } \right)\)
Cho hàm số \(y = f\left( x \right)\)xác định và liên tục trên \(\mathbb{R}\). Hàm số có bảng xét dấu của đạo hàm như sau:
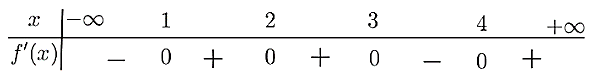
Số điểm cực trị của hàm số là
3
2.
1.
4
Cho hàm số \[y = f\left( x \right)\] liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;\,3} \right]\) như hình dưới đây.
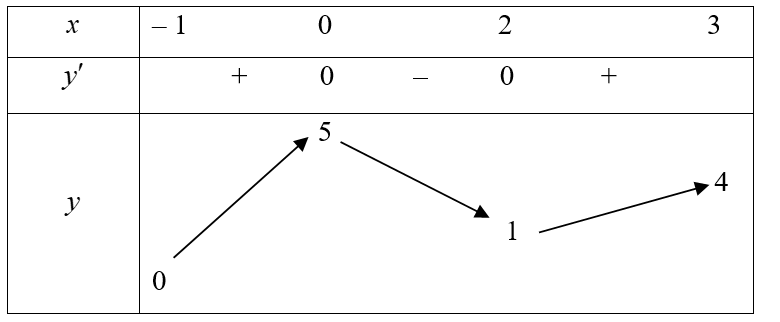
Gọi \(M\) là giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên đoạn \[\left[ { - 1;\,\,3} \right]\]. Mệnh đề nào trong các mệnh đề sau đây là đúng?
\[M = f\left( { - 1} \right)\].
\[M = f\left( 3 \right)\].
\(M = f\left( 2 \right)\).
\(M = f\left( 0 \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\backslash \left\{ 2 \right\}\) và có đồ thị như hình vẽ.
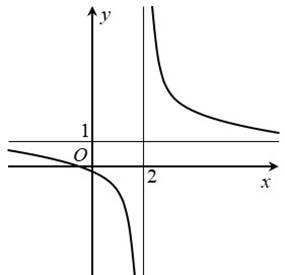
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
y=1
y=2
x=1
x=2
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
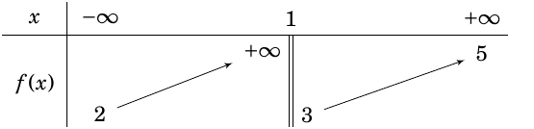
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
3
4
2
5
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
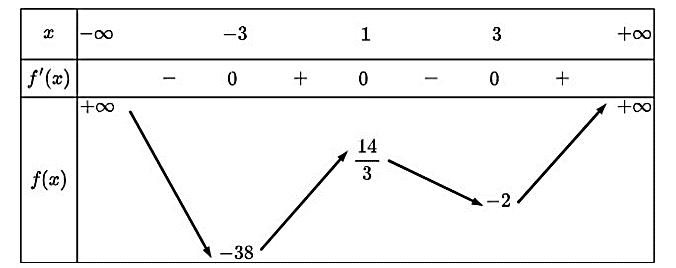
Đồ thị của hàm số trên cắt trục hoành tại bao nhiêu điểm?
1
2
3
4
Điểm nào sau đây thuộc đồ thị hàm số \(y = {x^4} - 2{x^2} - 1\)?
\(\left( { - 1; - 2} \right).\)
\(\left( {2; - 7} \right).\)
\(\left( {0;\,1} \right).\)
\(\left( {1;2} \right).\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Có bao nhiêu vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương bằng vectơ \(\overrightarrow {BC} \)?
3
4
2
1
Cho tứ diện ABCD, có bao nhiêu vectơ có điểm dầu là A và điểm cuối là một trong các đỉnh còn lại của tứ diện?
1
3
2
4
Hàm số \(y = {x^3} - 3x\) nghịch biến trên khoảng nào trong các khoảng dưới đây?
\(\left( { - \infty ;0} \right).\)
\(\left( { - 1;1} \right).\)
\(\left( {0; + \infty } \right).\)
\(\left( { - \infty ; + \infty } \right).\)
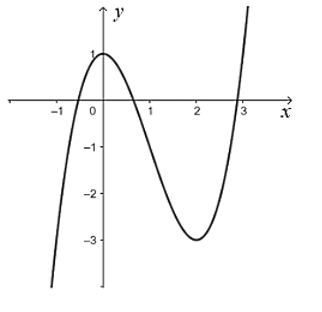
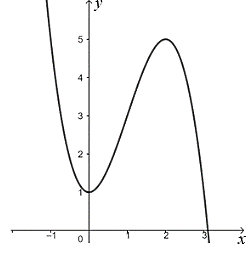
Đường cong nào dưới đây là đồ thị của hàm số \(y = {x^3} + x + 1\)?
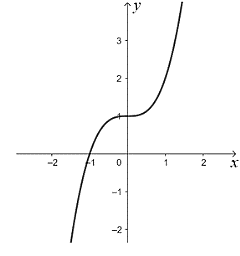
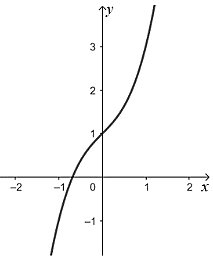
Cho lăng trụ \(ABC.A'B'C'\). Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \). Hãy biểu diễn vectơ \(\overrightarrow {B'C} \) theo \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)?
\(\overrightarrow {B'C} = \overrightarrow a + \overrightarrow b - \overrightarrow c .\)
\(\overrightarrow {B'C} = - \overrightarrow a + \overrightarrow b - \overrightarrow c .\)
\(\overrightarrow {B'C} = \overrightarrow a + \overrightarrow b + \overrightarrow c .\)
\(\overrightarrow {B'C} = - \overrightarrow a - \overrightarrow b + \overrightarrow c .\)
