11 câu hỏi
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ sau
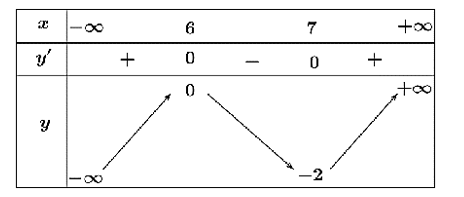
Điểm cực đại của hàm số \(y = f\left( x \right)\) là
\(x = 7\).
\(x = - 2\).
\(x = 0\).
\(x = 6\).
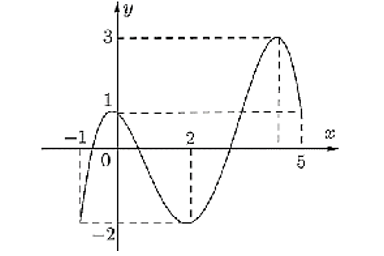
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\) bằng
\( - 1\).
\(4\).
\(1\).
\(2\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
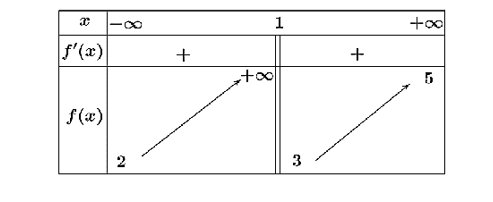
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
\(3\).
\(2\).
\(4\).
\(1\).
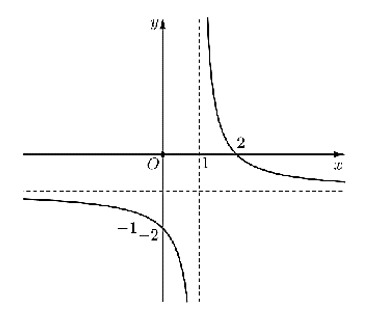
Cho hàm số \(y = \frac{{ax + b}}{{cx - 1}}\) có đồ thị như hình vẽ bên dưới. Giá trị của tổng \(S = a + b + c\) bằng
\(S = 0\).
\(S = - 2\).
\(S = 2\).
\(S = 4\).
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
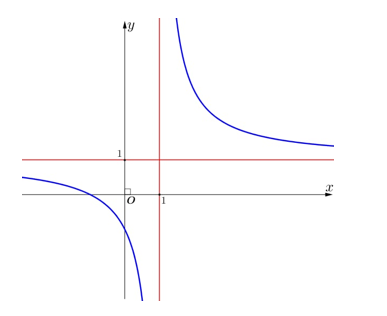
\(y = \frac{{x + 2}}{{x + 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{ - 2x + 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
Cho hình hộp \(ABCD.A'B'C'D'\). Tính tổng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A'C'} \).
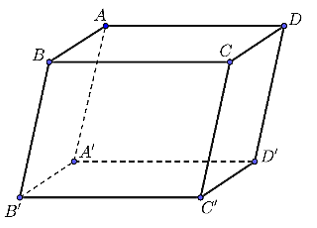
\(2\overrightarrow {AA'} \).
\(\overrightarrow 0 \).
\(2\overrightarrow {AC} \).
\(2\overrightarrow {C'A'} \).
Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(A\) thỏa mãn \(\overrightarrow {OA} = 2\overrightarrow i - 3\overrightarrow j + 4\overrightarrow k \) và \(B\left( {2;1;4} \right)\). Tọa độ của vectơ \(\overrightarrow {BA} \) là
\(\left( {0; - 4;0} \right)\).
\(\left( {4; - 2;8} \right)\).
\(\left( { - 1; - 1;2} \right)\).
\(\left( { - 2; - 2;4} \right)\).
Cho lăng trụ đứng \(ABC.A'B'C'\). Đáy là tam giác \(ABC\) vuông tại \(B\). Khi đó góc giữa vectơ \(\overrightarrow {BA} \) và vectơ \(\overrightarrow {B'C'} \) bằng bao nhiêu?
\(45^\circ \).
\(120^\circ \).
\(90^\circ \).
\(30^\circ \).
Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 3;5} \right)\). Tìm tọa độ \(A'\) là điểm đối xứng với \(A\) qua trục Oy.
\(A'\left( {2;3;5} \right)\).
\(A'\left( {2; - 3; - 5} \right)\).
\(A'\left( { - 2; - 3;5} \right)\).
\(A'\left( { - 2; - 3; - 5} \right)\).
Thời gian tập nhảy mỗi ngày trong thời gian gần đây của Cô Minh Hiền được thống kê lại ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
\(25\).
\(20\).
\(15\).
\(30\).
Xét mẫu số liệu ghép nhóm cho bởi bảng sau

Chọn khẳng định sai
Cỡ mẫu là \(n = {n_1} + {n_2} + ... + {n_k}\).
Số trung bình của mẫu số liệu ghép nhóm là \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\).
Phương sai của mẫu số liệu ghép nhóm là \({s^2} = \frac{1}{n}\left( {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2 - {{\overline x }^2}} \right)\).
Độ lệch chuẩn của mẫu số liệu ghép nhóm là căn bậc hai số học của phương sai.
